GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Chương 6. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
TOÁN 10 – CHƯƠNG TRÌNH MỚI
a) Định nghĩa: Cho một tập hợp khác rỗng
D
.
Nếu với mỗi giá trị của
x
thuộc tập hợp số
D
có một và chỉ một giá trị tương ứng của
thuộc tập số thực
thì ta có một hàm số.
• Ta gọi
x
là biến số và
là hàm số của
x
.
• Tập hợp
D
gọi là tập xác định của hàm số.
• Tập tất cả các giá trị
nhận được gọi là tập giá trị của hàm số thì ta nói
( )
|T f x x D=
là tập
giá trị của
( )
fx
trên
D
.
Chú ý:
• Cho
KD
thì ta nói
( )
|
K
T f x x K=
là tập giá trị của
( )
fx
trên
K
.
• Khi
y
là hàm số của
x
, ta có thể viết
( ) ( )
,,y f x y g x= =
b) Cách cho hàm số:
• Hàm số cho bằng công thức
( )
y f x=
Tập xác định của hàm số
( )
y f x=
là tập hợp tất cả các giá trị của
x
để
( )
fx
có nghĩa.
• Hàm số cho bằng nhiều công thức.
• Hàm số không cho bằng công thức.
Đồ thị của hàm số
( )
y f x=
xác định trên tập
D
là tập hợp tất cả các điểm
( )
( )
;M x f x
trên mặt phẳng
toạ độ với mọi
x
thuộc
D
hay ta có thể diễn tả bằng:
( ) ( ) ( )
0 0 0 0
;M x y G y f x =
với
0
xD
.
Ta thường gặp đồ thị của hàm số
( )
y f x=
là một đường. Khi đó ta có
( )
y f x=
là phương trình của đường
đó.
C
H
Ư
Ơ
N
G
6
HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
HÀM SỐ
01
BÀI
LÝ THUYẾT CẦN NHỚ
A
1
Định nghĩa
2
Đồ thị hàm số
GV. Phan Nhật Linh -
SĐT: 0817 098 716
2
Chương 6. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
TOÁN 10 – CHƯƠNG TRÌNH MỚI
a) Khái niệm: Cho hàm số
( )
y f x=
xác định trên
K
.
• Hàm số
( )
y f x=
gọi là đồng biến (hay tăng) trên
K
nếu:
12
,x x K
và
12
xx
( ) ( )
12
f x f x
.
• Hàm số
( )
y f x=
gọi là nghịch biến (hay giảm) trên
K
nếu:
12
,x x K
và
12
xx
( ) ( )
12
f x f x
.
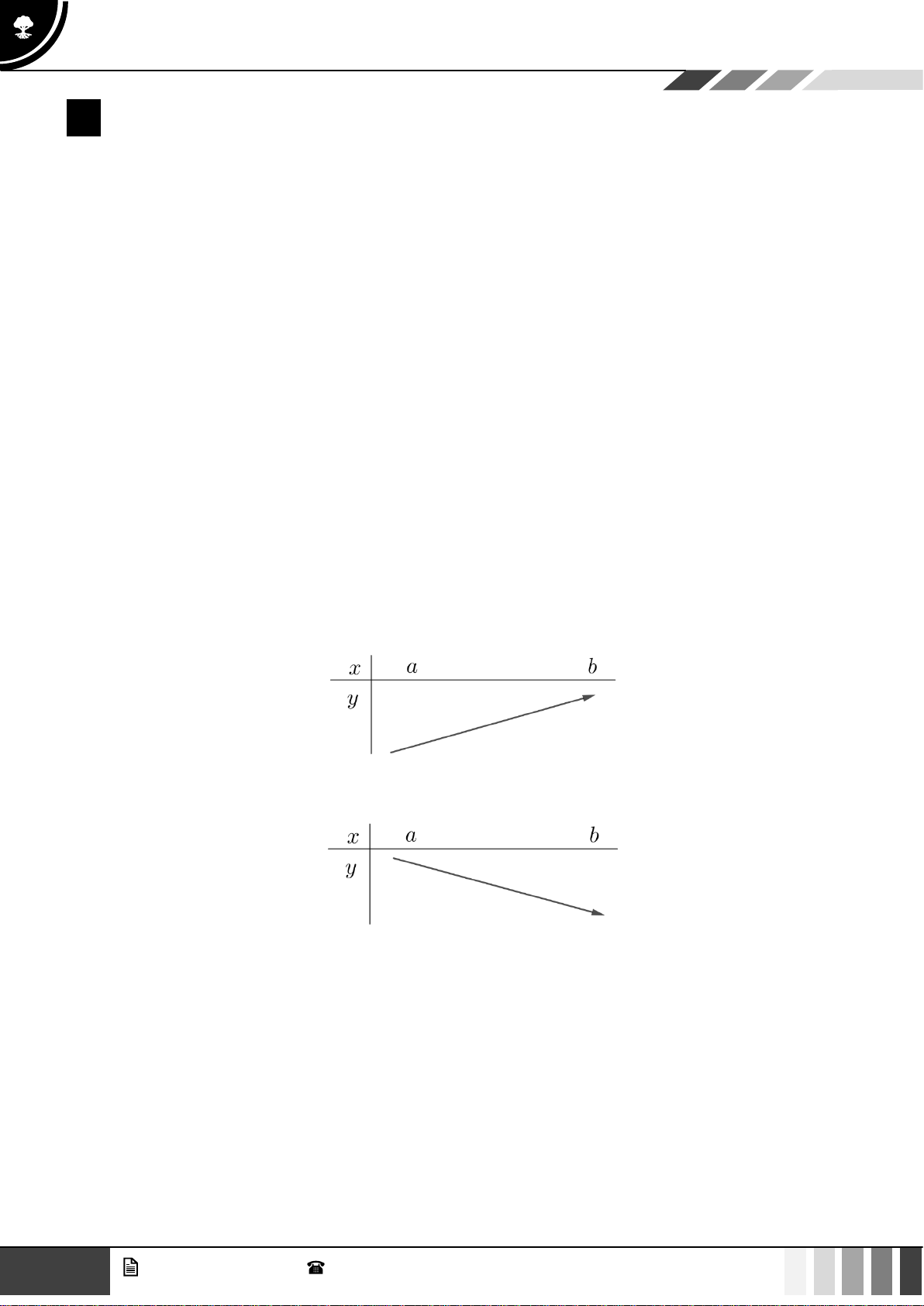
b) Mô tả hàm số đồng biến, hàm số nghịch biến bằng đồ thị
• Hàm số
( )
y f x=
đồng biến trên
( )
;ab
khi và chỉ khi đồ thị hàm số “đi lên” trên khoảng đó.
• Hàm số
( )
y f x=
nghịch biến trên
( )
;ab
khi và chỉ khi đồ thị hàm số “đi xuống” trên khoảng đó.
c) Bảng biến thiên: Hàm số
( )
y f x=
xác định trên
( )
;ab
.
• Xét chiều biến thiên của hàm số là tìm khoảng tăng, giảm của hàm số.
• Kết quả đó được tổng kết trong một bảng gọi là bảng biến thiên
• Đồ thị hàm số đồng biến trên
( )
;ab
là một đường “đi lên” trong khoảng
( )
;ab
.
• Đồ thị hàm số nghịch biến trên
( )
;ab
là một đường “đi xuống” trong khoảng
( )
;ab
3
Sự đồng biến, nghịch biến của hàm số
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Chương 6. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
TOÁN 10 – CHƯƠNG TRÌNH MỚI
Dạng 1: Tìm tập xác định của hàm số
Phương pháp: Để tìm tập xác định của hàm số ta cần nhớ như sau
( )
1
fx
xác định
( )
0fx
( )
fx
xác định
( )
0fx
( )
( )
fx
gx
xác định
( )
0gx
Bài toán chứa tham số: Cho hàm
( )
,y f x m=
. Tìm tất cả các giá trị tham số
m
để hàm số xác định
trên tập
K
.
Bước 1: Tìm điều kiện xác định của hàm số theo
m
. Gọi
D
là tập xác định của hàm số.
Bước 2: Hàm số xác định trên tập
K
khi và chỉ khi
KD
.
Chú ý: Cho
A
là biểu thức luôn có nghĩa:
• Hàm số
( )
,
A
yf x m
=
xác định trên
K
( )
,0f x m =
vô nghiệm trên
K
.
• Hàm số
( )
,y f x m=
xác định trên
K
( )
,0f x m x K
• Hàm số
( )
,
A
yf x m
=
xác định trên
K
( )
,0f x m x K
Bài tập 1: Tìm tập xác định của các hàm số sau:
a)
32
2 3 2025y x x= − +
b)
21
1x
yx
−
=−
c)
2
1
45
yxx
=++
d)
2
21
32
x
yxx
−
=−+
e)
2
2
5
x
yx
+
=−
f)
2
2
45
x
yxx
=−−
g)
2
2
4
yx
=−
h)
221
91
x
yxx
+
=−
−−
i)
13 2 1
x
yx
x
−
= − − +
j)
221
2
x
yxx
−
=−−
k)
2
2
14
2
xx
yxx
− − −
=−−
l)
2
156
52
xx
yxx
x
−
=−
−+
−
Bài tập 2: Tìm tập xác định của các hàm số sau:
a)
32yx=−
b)
21yx=+
c)
2 1 1y x x= − + − −
d)
22 1 3y x x x= − + + −
e)
22
3 2 2 2 2 1y x x x x= + + + + − + −
f)
21y x x x= + − +
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN
B
BÀI TẬP TỰ LUẬN
GV. Phan Nhật Linh -
SĐT: 0817 098 716
4
Chương 6. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
TOÁN 10 – CHƯƠNG TRÌNH MỚI
Bài tập 3: Cho hàm số
2
21x
yx x m
+
=++
. Tìm tất cả các giá trị của
m
để hàm số xác định trên .
Bài tập 4: Cho hàm số
2y x m=−
. Tìm các giá trị của
m
để hàm số có tập xác định là
)
2;+
Bài tập 5: Cho hàm số
3 5 6
1
xm
yxm
−+
=+−
. Tìm các giá trị của
m
để hàm số xác định trên
( )
0;+
Bài tập 6: Cho hàm số
21y m x x m= − + − +
. Tìm các giá trị của
m
để hàm số xác định trên
( )
0;1
.
Bài tập 7: Cho hàm số
( )
4 3 2
4 5 4 4y x x m x x m= + + + + + +
. Tìm các giá trị của
m
để hàm số xác định
trên .
Bài tập 8: Với giá trị nào của
m
thì hàm số
2
21
23
x
yx x m
+
=− − −
xác định trên .
A.
4m−
. B.
4m−
. C.
0m
. D.
4m
.
Bài tập 9: Tìm tất cả các giá trị của
m
để hàm số
1
2 3 2 24
x
y x m xm
+
= − + + + +−
xác định trên
( )
;2− −
.
Bài tập 10: Tập tất cả các giá trị
m
để hàm số
2
1
23
y x m
xx
= + −
− − +
có tập xác định khác tập rỗng.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Chương 6. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
TOÁN 10 – CHƯƠNG TRÌNH MỚI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
Câu 1: Trong các hàm số sau, hàm số nào có tập xác định là ?
A.
32
31y x x= + −
. B.
22x
yx
+
=
. C.
2
23x
yx
+
=
. D.
2
1
x
yx
+
=−
.
Câu 2: Tập xác định của hàm số
1
1
x
yx
+
=−
là:
A.
\1
. B.
\1−
. C.
\1
. D.
( )
1; +
.
Câu 3: Tập xác định của hàm số
( )
2
2
3
x
yx
+
=−
là
A.
( )
;3−
. B.
( )
3;+
. C.
\3
. D. .
Câu 4: Tập xác định của hàm số
2
356
x
yxx
−
=−−
là
A.
\ 1;6D=−
B.
\ 1; 6D=−
C.
1;6D=−
D.
1; 6D=−
Câu 5: Tìm tập xác định D của hàm số
( )
( )
2
1
14
x
yxx
+
=+−
.
A.
\2D=
B.
\2D=
C.
\ 1;2D=−
D.
\ 1; 2D= −
Câu 6: Tập xác định
D
của hàm số
31yx=−
là
A.
( )
0;D= +
. B.
)
0;D= +
. C.
1;
3
D
= +

. D.
1;
3
D
= +


.
Câu 7: Tập xác định của hàm số
34
1
x
yx
+
=−
là
A.
\1
. B. . C.
( )
1; +
. D.
)
1; +
.
Câu 8: Tìm tập xác định
D
của hàm số
19 5
18 90
x
yx
+
=−
là
A.
D=
. B.
\5D=−
. C.
\5D=
. D.
\5D=
.
Câu 9: Tìm tập xác định
D
của hàm số
29yx=−
.
A.
9
\2
D
=

. B.
9
;2
D
= −

. C.
9;
2
D
= +


. D.
9;
2
D
= +

.
Câu 10: Tìm tập xác định
D
của hàm số
2212
x
yxx
+
=+−
.
A.
)
2; \ 4D= − + −
. B.
)
2;D= − +
. C.
\ 4;3D=−
. D.
)
2; \ 3D= − +
.
Câu 11: Hàm số nào trong các hàm số dưới đây có tập xác định là ?
A.
21
42
x
yx
−
=−
. B.
1yx=−
. C.
2
31
x
yx
=+
. D.
2
1
22
x
yxx
−
=−+
.
Câu 12: Tập tất cả các giá trị
m
để hàm số
2y x m m x= − + −
xác định trên khoảng
( )
2;3
.
BÀI TẬP TRẮC NGHIỆM