Chuyên đề Xác định các hệ số của hàm số nhất biến

Tài liệu này thuộc chuyên đề xác định hệ số của hàm số bậc nhất, được sưu tầm vào ngày 8 tháng 12 năm 2020. Tài liệu này tập trung vào việc xác định dấu của các hệ số trong hàm số bậc nhất dựa trên bảng biến thiên và các đặc điểm của đồ thị hàm số, như tiệm cận đứng, tiệm cận ngang và tính đơn điệu.

Tài liệu này hướng đến học sinh THPT và giáo viên dạy toán, đặc biệt hữu ích cho việc ôn thi THPT Quốc gia, giúp nắm vững phương pháp xác định hệ số hàm số từ đồ thị và bảng biến thiên.

Tài liệu này cung cấp phương pháp xác định hệ số của hàm số bậc nhất dựa trên bảng biến thiên và các đặc điểm của đồ thị. Cụ thể, nó trình bày cách xác định dấu của các hệ số a, b, c trong hàm số f(x) = (ax + 1)/(bx + c) thông qua việc phân tích tiệm cận đứng, tiệm cận ngang và chiều biến thiên của hàm số.

1. **Phương pháp chung:**
* Từ công thức hàm số, xác định phương trình tiệm cận đứng, tiệm cận ngang và công thức đạo hàm.
* Từ bảng biến thiên, xác định tiệm cận đứng, tiệm cận ngang và chiều biến thiên.
* Kết hợp các dữ kiện để xác định dấu của các hệ số.

2. **Ví dụ minh họa:**
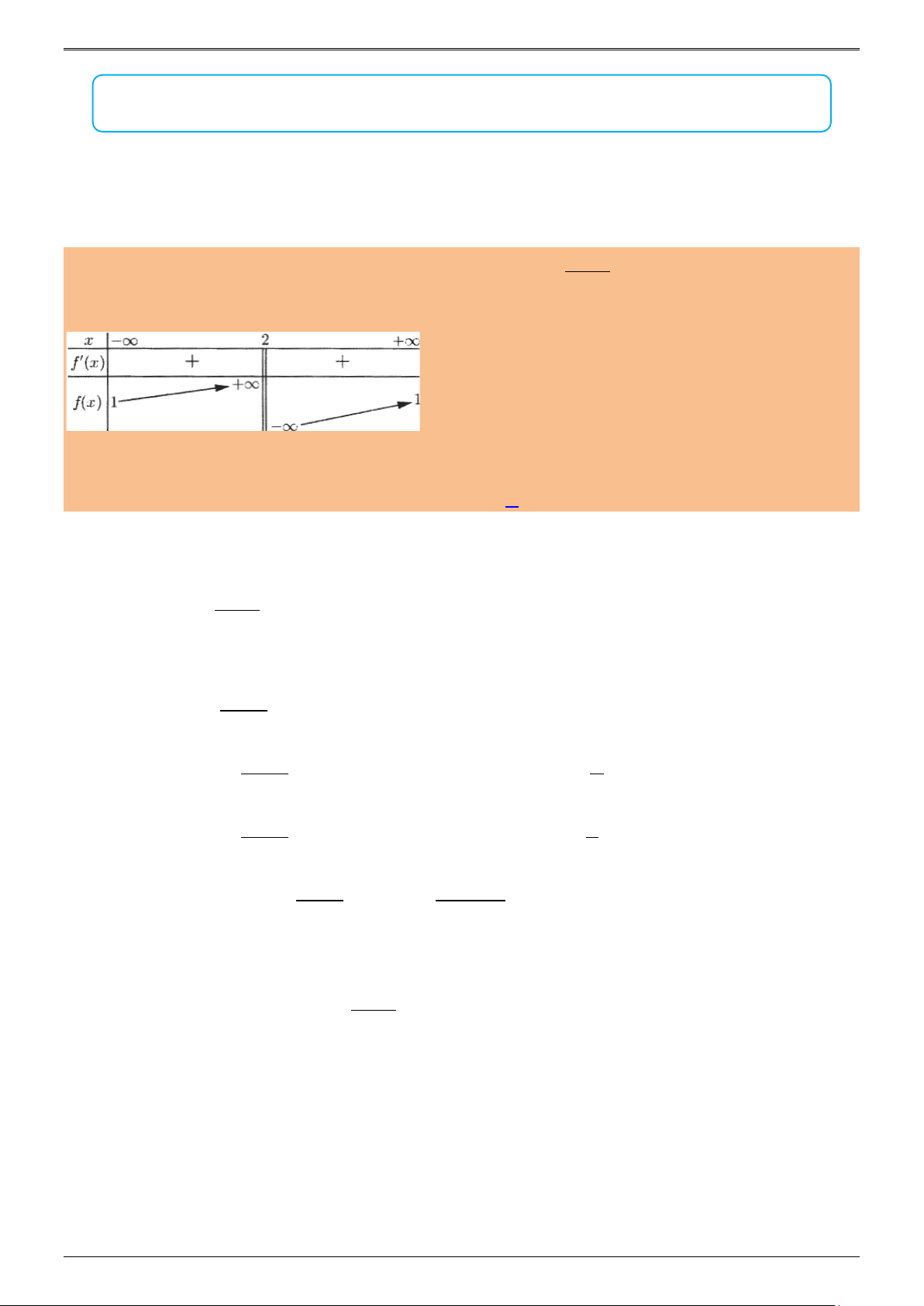
* Cho hàm số f(x) = (ax + 1)/(bx + c) với bảng biến thiên. Xác định dấu của a, b, c.
* Lời giải chi tiết sử dụng tiệm cận và đạo hàm để suy ra mối quan hệ giữa các hệ số.

3. **Bài tập tương tự và phát triển:**
* Một loạt các bài tập với độ khó tăng dần, bao gồm cả các bài toán liên quan đến hàm số bậc hai, bậc ba và các hàm số hữu tỉ khác.
* Các bài tập này yêu cầu xác định dấu của các hệ số, tìm mệnh đề đúng, viết phương trình tiếp tuyến, và giải các bài toán liên quan đến đồ thị hàm số.

4. **Các dạng toán thường gặp**
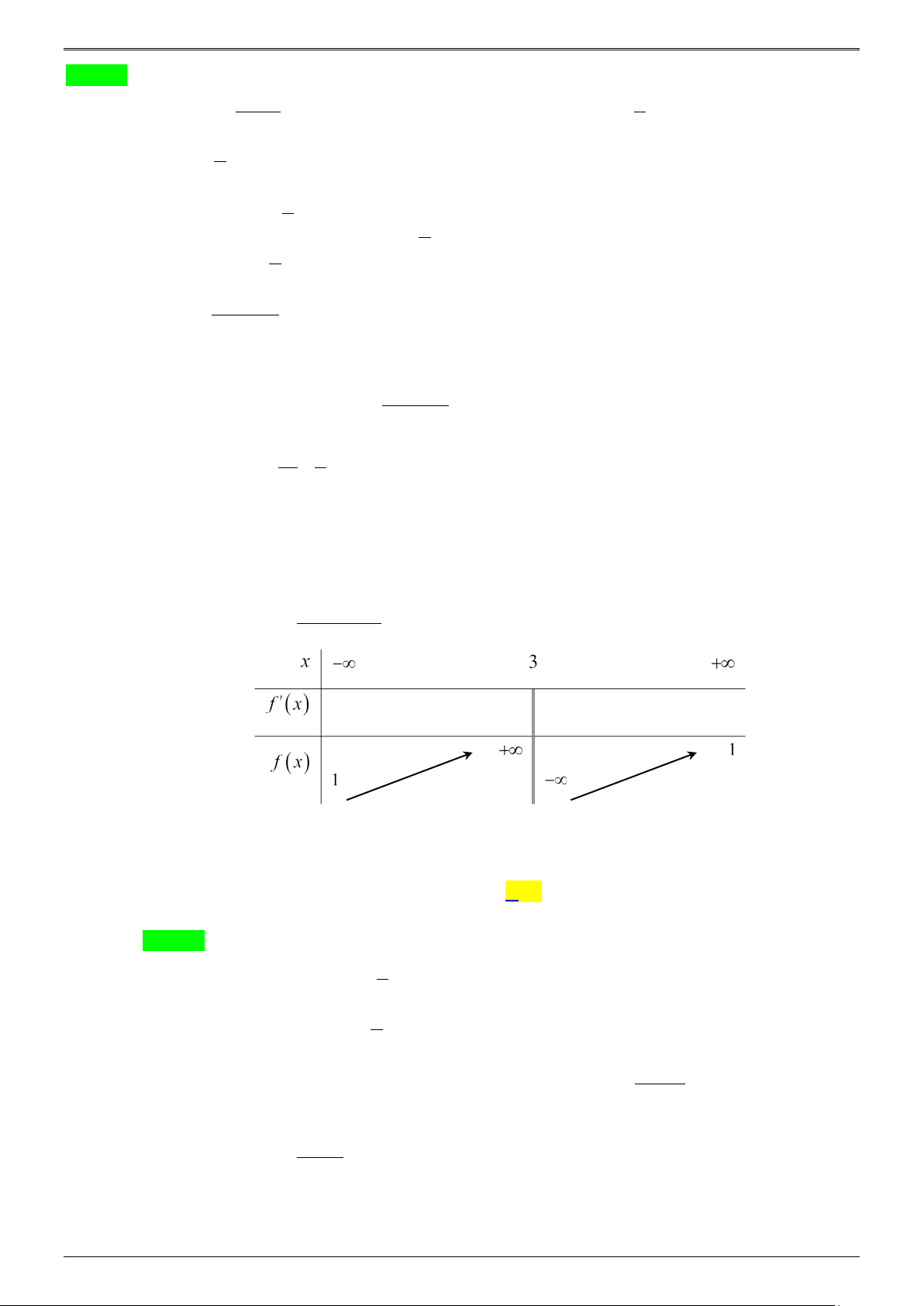
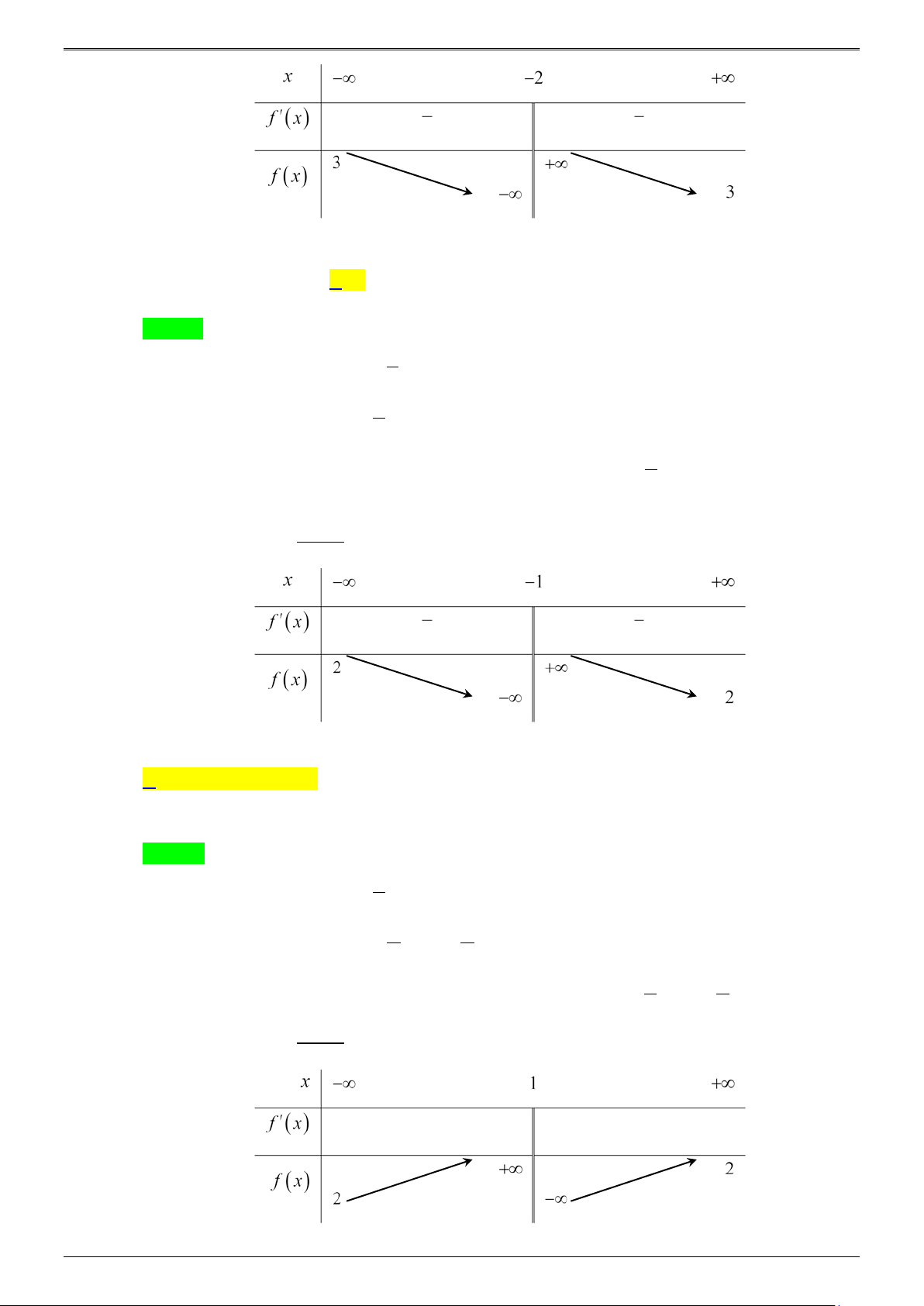
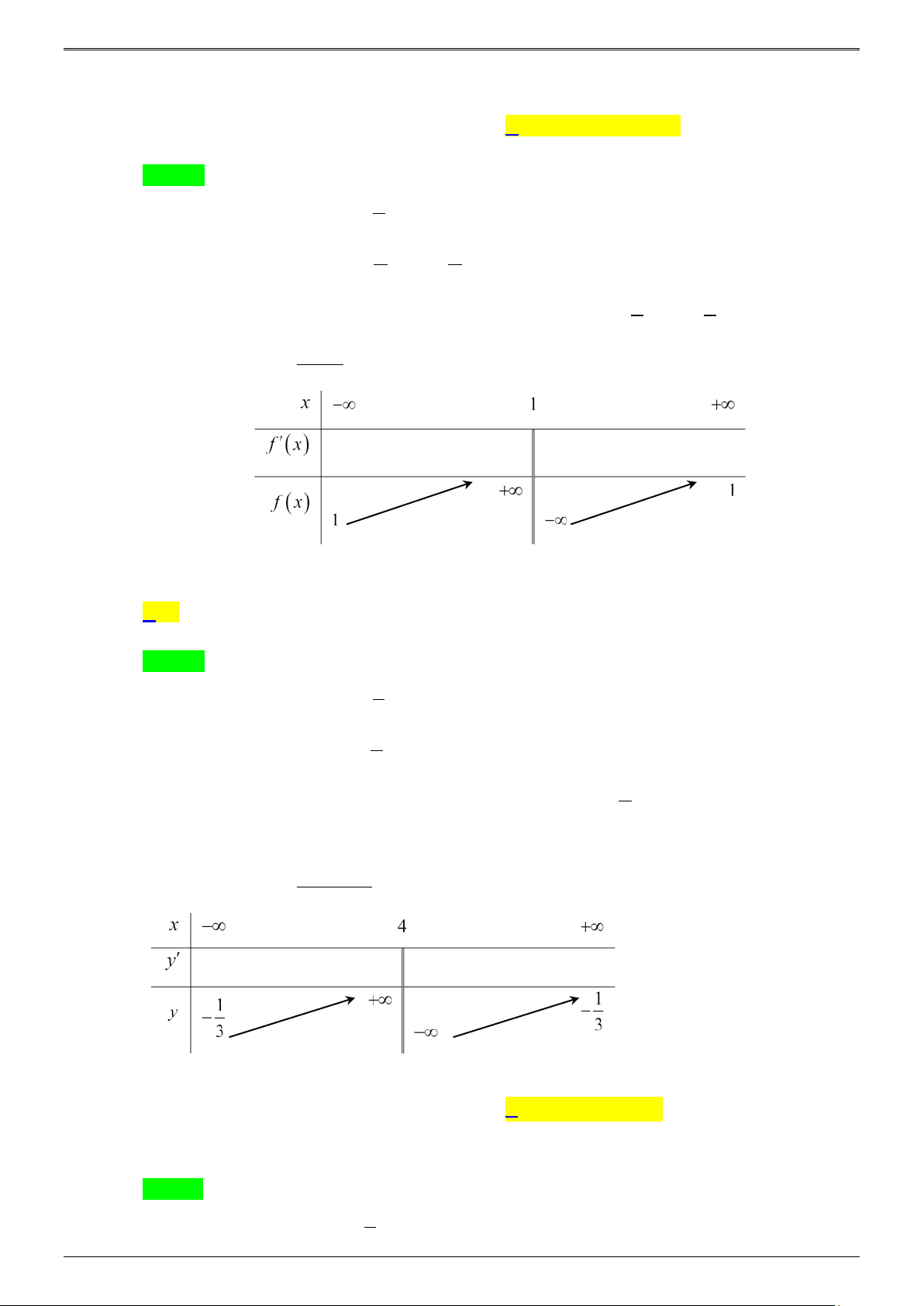
* Tìm các hệ số dựa trên bảng biến thiên
* Tìm các hệ số dựa trên đồ thị hàm số
* Biện luận số nghiệm dựa trên đồ thị
* Viết phương trình tiếp tuyến