§2.5 Các đ c tính c a đ ng c không đ ng b ba phaặ ủ ộ ơ ồ ộ
I. Các đ c tính : ặ
S đ nguyên lý c a đông c không đ ng b : bao g m đ ng c không đ ng b ro to dây qu n và roto l ngơ ồ ủ ơ ồ ộ ồ ộ ơ ồ ộ ấ ồ
sóc:
Đ ngộ c không đ ng b có k t c u đ n gi n, nh ng vi c kh ng ch nó trong quá trình kh i đ ng, đi uơ ồ ộ ế ấ ơ ả ư ệ ố ế ở ộ ề
ch nh t c đ và quá trình hãm là r t ph c t p. Đ c bi t là khi đ ng c làm vi c trong vùng bão hoà t thìỉ ố ộ ấ ứ ạ ặ ệ ộ ơ ệ ừ
các đ c tính c a nó đ u là phi tuy n. Do v y đ đ n gi n khi nghiên c u đ ng c không đ ng b ba phaặ ủ ề ế ậ ể ơ ả ứ ộ ơ ồ ộ
c n có các gi thi t sau :ầ ả ế
+ Ba pha c a đ ng c là đ i x ng ủ ộ ơ ố ứ
+ Các thông s c a m ch không thay đ i nghĩa là không ph thu c vào nhi t đ , đi n tr m ch rôtoố ủ ạ ổ ụ ộ ệ ộ ệ ở ạ
không ph thu c vào t n s dòng đi n trong nó, m ch t không bão hào ...ụ ộ ầ ố ệ ạ ừ
+ T ng d n c a m ch vòng t hoá không thay đ i , dòng đi n t hoá ch ph thu c vào đi n áp đ t vàoổ ẫ ủ ạ ừ ổ ệ ừ ỉ ụ ộ ệ ặ
stato c a đ ng c ủ ộ ơ
+ B qua các t n th t do ma sát , t n th t trong lõi thép ỏ ổ ấ ổ ấ
+ Đi n áp là hoàn toàn hình sin và đ i x ng ệ ố ứ
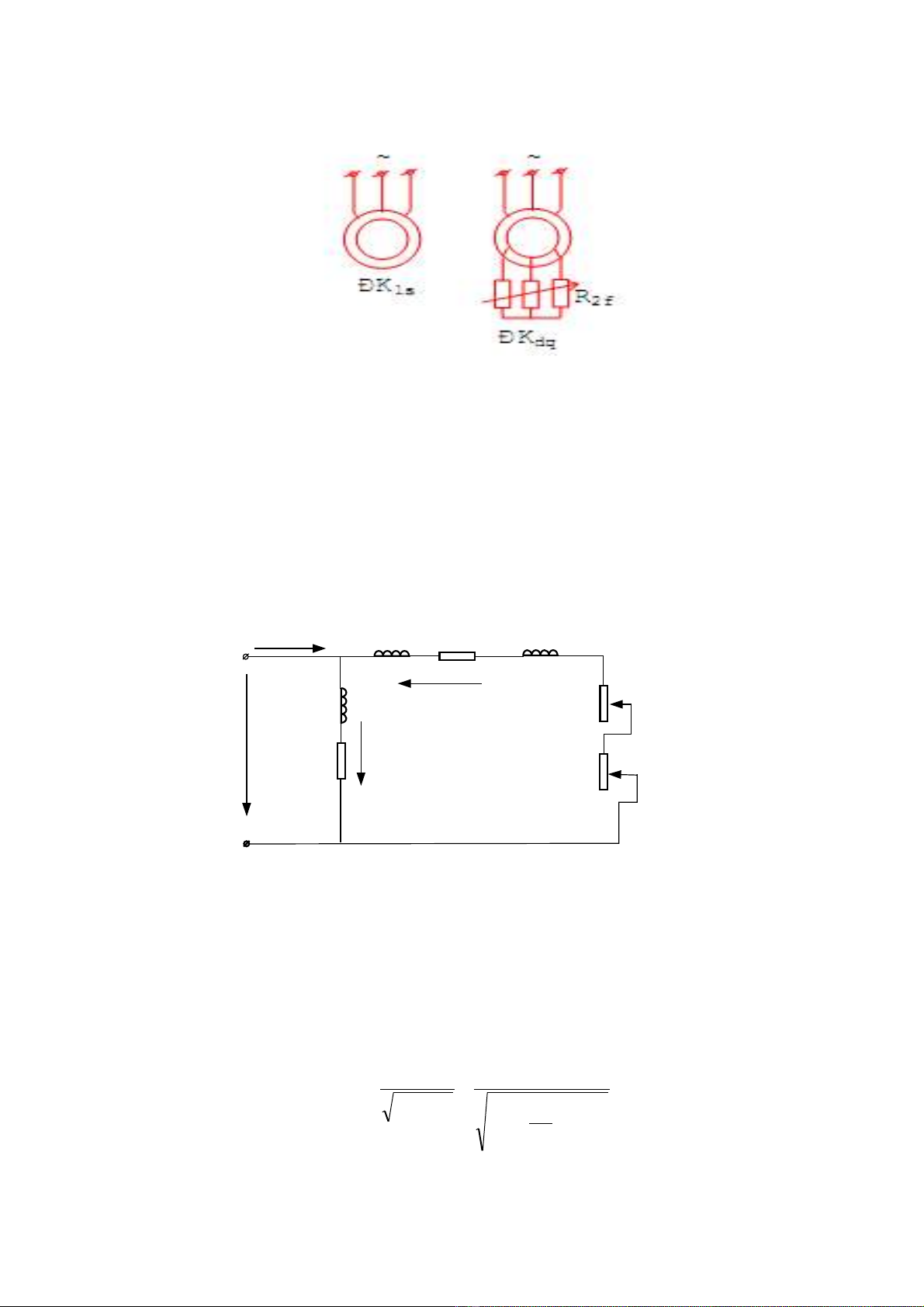
V i các gi thi t trên ta có s đ thay th c a đ ng c KĐB ba pha nh sau :ớ ả ế ơ ồ ế ủ ộ ơ ư
I
1
I
2
I
μ
x
1
r
1
x
2
'
r
2
'/s
R
f
’/s
r
μ
x
μ
U
1
Trong đó:
U1 : Tr s hi u d ng đi n áp pha statoị ố ệ ụ ệ ở
I1 , Iμ , I2 : Tr s dòng đi n stato , dòng t hoá , dòng đi n roto qui đ i v statoị ố ệ ừ ệ ổ ề
r1 , rμ , r2’ : Tr s đi n tr stato , đi n tr m ch t hoá , đi n tr roto qui đ i v statoị ố ệ ở ệ ở ạ ừ ệ ở ổ ề
x1 , xμ , x2’ : Tr s đi n kháng stato , đi n kháng m ch t hoá , đi n kháng roto qui đ i v statoị ố ệ ệ ạ ừ ệ ổ ề
Rf’ : Đi n tr ph thêm vào m i pha c a rotoệ ở ụ ỗ ủ
s : Đ tr t c a đ ng c ộ ượ ủ ộ ơ
T s đ thay th ta có tr s hi u d ng g n đúng c a dòng đi n stato: ừ ơ ồ ế ị ố ệ ụ ầ ủ ệ
+
+
+
+
=
2
'
2
1
22
11
11
nm
x
s
R
r
xr
UI
µµ
Trong đó
'
21
''
2
'
2;xxxRrR nmf +=+=
: đi n kháng ng n m ch .ệ ắ ạ
T bi u th c trên ta nh n th y :ừ ể ứ ậ ấ
1
ω = 0 ; s = 1 ta có I1 = I1nm : dòng đi n ng n m ch statoệ ắ ạ
ω = ω0 ; s = 0
+
=22
11
1
µµ
xr
UI
= Iμ
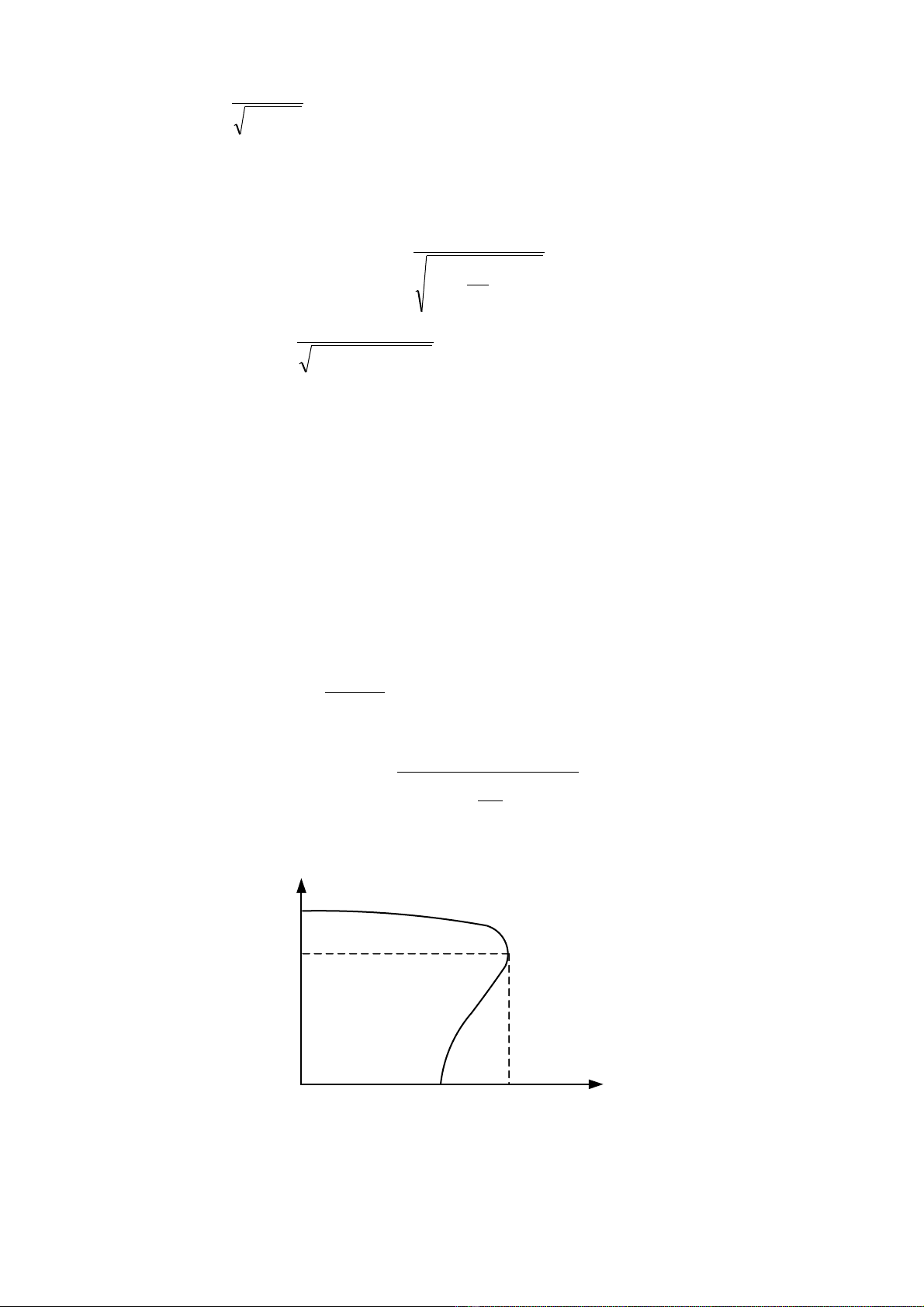
Nghĩa là t c đ đ ng b đ ng c v n tiêu th dòng đi n t hoá đ t o ra t tr ng quay . Ta có đ cở ố ộ ồ ộ ộ ơ ẫ ụ ệ ừ ể ạ ừ ườ ặ
tính dòng đi n stato đ c trình bày nh sau :ệ ượ ư
Tr s dòng đi n roto quy đ i v stato là ị ố ệ ổ ề
2
'
2
1
1
'
2
nm
x
s
R
r
U
I
+
+
=
ω = 0 ; s = 1 ta có
'
2
2'
21
1
'
2
)(
nm
nm
I
xRr
U
I
=
++
=
ω = ω0 ; s = 0 I2’ = 0
Đ c tính dòng đi n stato đ c trình bày nh sau :ặ ệ ượ ư
Đ tìm ph ng trình đ c tính c ta xu t phát t đi u ki n cân b ng công su t trong đ ng c , công su tể ươ ặ ơ ấ ừ ề ệ ằ ấ ộ ơ ấ
đi n t chuy n t stato sang rôto :ệ ừ ể ừ
0
.
dt dt
P M
ω
=
v i Mớđt là mô men đi n t c a đ ng c . N u b qua các t n th t ph thì ta có Mệ ừ ủ ộ ơ ế ỏ ổ ấ ụ đt = Mcơ và ta có Mđt = Mcơ
= M .
Công su t đó đ c chia làm hai thành ph n đó là : Công su t c trên tr c đ ng c Pấ ượ ầ ấ ơ ụ ộ ơ cơ và công su t t n haoấ ổ
đ ng trong roto là ồΔP2
P12 = Pcơ + ΔP2
MΔP2 = Mω + ΔP2
Do đó ta có ΔP2 = M ( ω0 - ω ) = Mω0s
M t khác ặΔP2 = 3I2’2 R2’ nên
s
RU
M
0
'
2
2
1
3
ω
=
Khi thay th vào ta có ph ng trình đ c tính c nh sauế ươ ặ ơ ư
M i quan h M = f (ố ệ ω) là m t đ ng cong có c c tr , d ng c a nó đ c bi u di n trên hình v .ộ ườ ự ị ạ ủ ượ ể ễ ẽ
M
n
M
th
s
th
Đi m c c tr đ c g i là đi m t i h n có to đ [ Mể ự ị ượ ọ ể ớ ạ ạ ộ th , sth ] , các giá tr đó đ c xác đ nh nh sauị ượ ị ư
2
'
2
2 2
1
2
1
2 2
0 1 1
3
2 ( )
th
nm
th
nm
R
s
r x
U
M
r r x
ω
= ± +
= ± ± +
Trong bi u th c trên d u + ng v i tr ng thái đ ng c còn d u - ng v i tr ng thái máy phátể ứ ấ ứ ớ ạ ộ ơ ấ ứ ớ ạ
Ph ng trình đ c tính c còn đ c vi t d ng sau :ươ ặ ơ ượ ế ở ạ
th
th
1
'
2
2 (1 as
2as
th
th
th
M
Ms
s
s s
r
aR
+
=+ +
=
- Đ i v i nh ng đ ng c có công su t l n thì rố ớ ữ ộ ơ ấ ớ 1 r t nh h n so v i xấ ỏ ơ ớ nm nên ta có th coi rể1 =0 khi đó ta có
2
th
th
th
M
Ms
s
s s
=+
Và
'
2
2
1
0
3
2
th
nm
th
nm
R
sx
U
Mx
ω
= ±
= ±
- Trong nhi u tr ng h p cho phép ta s d ng nh ng ph ng trình g n đúng b ng cách tuy n tính hoá đ cề ườ ợ ử ụ ữ ươ ầ ằ ế ặ
tính c trong đo n làm vi c . nh ng vùng có đ tr t s < 0,4 ta xem nh ơ ạ ệ Ở ữ ộ ượ ư
0
th
s
s
=
và khi đó ta có ph ngươ
trình đ c tính c ặ ơ
2
th
th
M
M s
s
=
- Có th tuy n tính hoá đo n đ c tính làm vi c qua hai đi m làm vi c là đi m không t i và đi m làm vi cể ế ạ ặ ệ ể ệ ể ả ể ệ
đ nh m c . Ph ng trình có d ng g n đúng nh sau ị ứ ươ ạ ầ ư
dm
2
dm
M
M s
s
=
- Đ c ng c a đ c tính c ộ ứ ủ ặ ơ
ĐTC c a đ ng c bi n đ i c v tr s l n d u , vì v y khi xét ta ch xét cho t ng đo n đ c tính ủ ộ ơ ế ổ ả ề ị ố ẫ ấ ậ ỉ ừ ạ ặ
dM dM ds
d ds d
βω ω
= = •
II. Các thông s nh h ng đ n đ c tính c ố ả ưở ế ặ ơ
1. nh h ng c a thông s di n áp Ả ưở ủ ố ệ
Khi đi n áp thay đ i đ tr t t i h n c a đ ng c không thay đ i , còn mô men t i h n c a đ ng c thayệ ổ ộ ượ ớ ạ ủ ộ ơ ổ ớ ạ ủ ộ ơ
đ i t l v i bình ph ng c a đi n áp l i ổ ỷ ệ ớ ươ ủ ệ ướ
'
2
2
1
0
onst
3ar
2
th
nm
th
nm
R
s c
x
U
M v
x
ω
= ± =
= ± =
N u đi n áp đ vào đ ng c gi m quá th p có th làm cho mô men kh i đ ng c a đ ng c gi m th p vàế ệ ặ ộ ơ ả ấ ể ở ộ ủ ộ ơ ả ấ
đ ng c s không kh i đ ng đ c ộ ơ ẽ ở ộ ượ
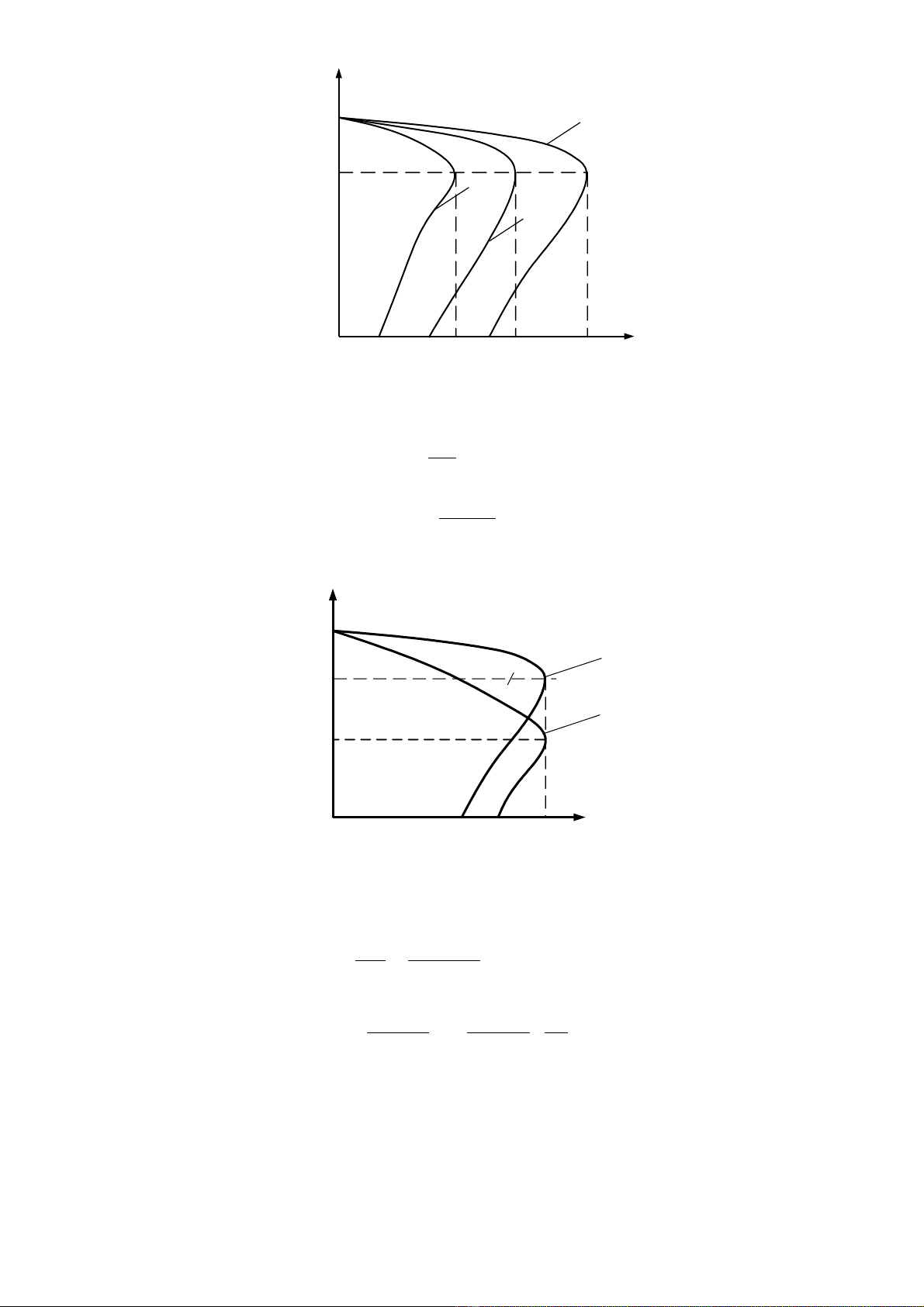
Khi gi m áp ta s thu đ c m t h đ ng đ c tính c nh sau :ả ẽ ượ ộ ọ ườ ặ ơ ư
3
ω
0
đt.tn
M
th
M
th.u
U
1
U
2
ω
th
ω
M
2. nh h ng c a thông s đi n tr ph m ch rotoẢ ưở ủ ố ệ ở ụ ạ
Khi thay đ i đi n tr m ch rôto thì đ tr t t i h n c a đ ng c thay đ i , còn mô men t i h n c aổ ệ ở ạ ộ ượ ớ ạ ủ ộ ơ ổ ớ ạ ủ
đ ng c không thay thay đ i ộ ơ ổ
'
2
2
1
0
ar
3onst
2
th
nm
th
nm
R
s v
x
U
M c
x
ω
= ± =
= ± =
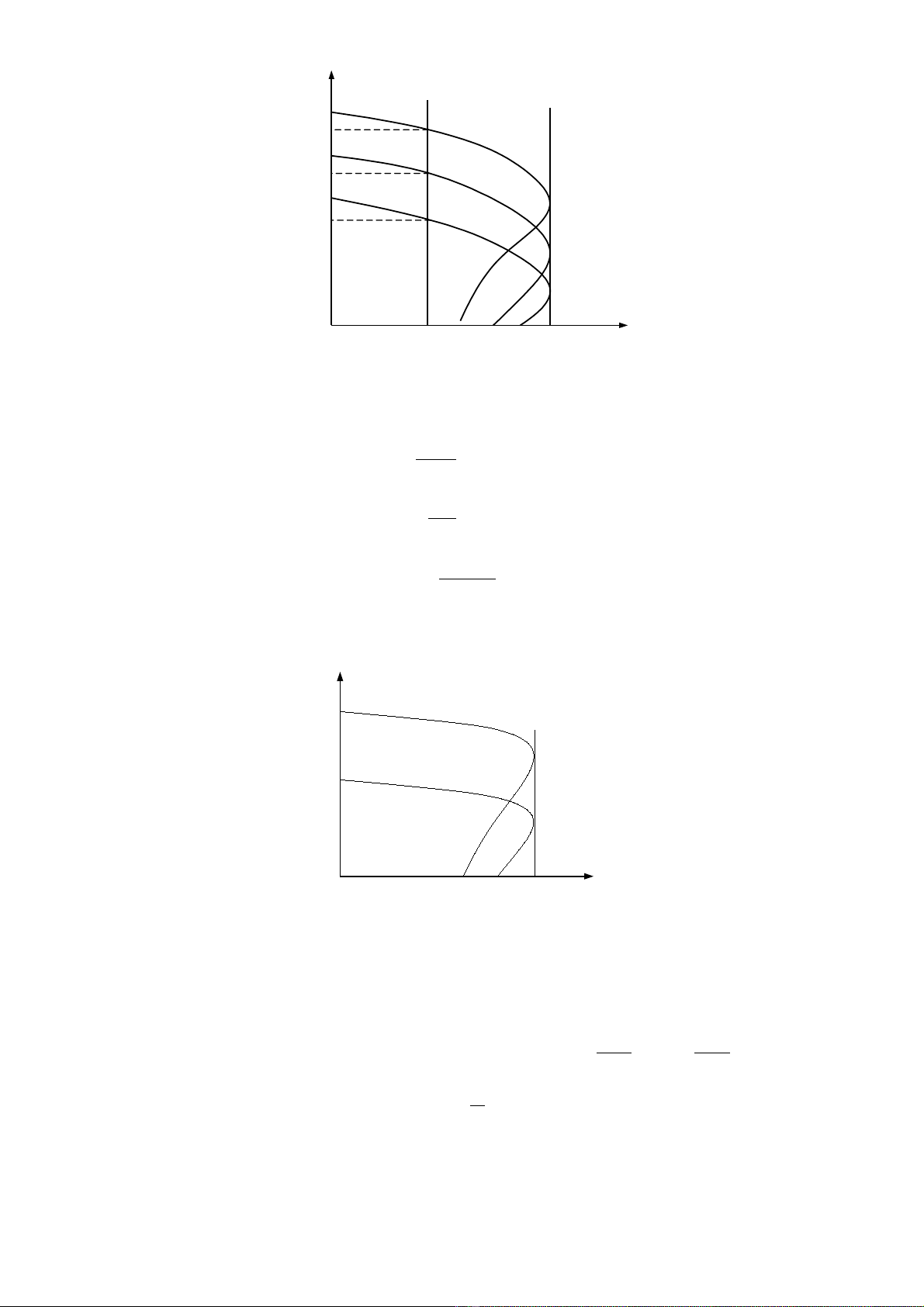
H đ ng đ c tính thu đ c khi thay đ i nh sau ọ ườ ặ ượ ổ ư
đt.tn
ω
M
M
th
đt.bt
ω
0
M
1
ω
th1
ω
th1
3. nh h ng c a thông s t n s ngu n đi n Ả ưở ủ ố ầ ố ồ ệ
N u cung c p cho đ ng c b ng m t ngu n đi n có t n s thay đ i thì t c đ đ ng c thay đ i và d ngế ấ ộ ơ ằ ộ ồ ệ ầ ố ổ ố ộ ộ ơ ổ ạ
đ c tính c cũng thay đ i ặ ơ ổ
' '
2 2
1
2
2
1 1
2
0 1
ar
2
3 3 ar
2 8
th
nm nm
th
nm nm
R R
s v
x f L
U U
M v
x L f
π
ω π
= ± = =
= ± = ± =
Nh v y mô men t i h n thay đ i theo s thay đ i c a t s U1/f1 . N u ta gi cho t s này không đ iư ậ ớ ạ ổ ự ổ ủ ỷ ố ế ữ ỷ ố ổ
thì Mth cũng không thay đ i ổ
4
M
ω
f
1
f
đm
f2
ω
1
ω
đm
ω
2
M
th
M
C
4. nh h ng c a s đôi c c pẢ ưở ủ ố ự
Đ i v i nh ng đ ng c không đ ng b roto l ng sóc nhi u c p t c đ đ đi u ch nh t c đ ng i ta thayố ớ ữ ộ ơ ồ ộ ồ ề ấ ố ộ ể ề ỉ ố ộ ườ
đ i thông s đôi c c c a máy ổ ố ự ủ
Khi thay đ i s đôi c c p ta có ổ ố ự
1
0
'
2
2
1
0
2ar
onst
3onst
2
th
nm
th
nm
fv
p
R
s c
x
U
M c
x
π
ω
ω
= =
= ± =
= ± =
V i nh ng đ ng c mà thay đ i s đôi c c b ng cách thay đ i cách đ u các cu n dây stato thi Mớ ữ ộ ơ ổ ố ự ằ ổ ấ ộ th có thể
b thay đ i . H đ ng đ c tính c thu đ c khi thay đ i p = 1; p = 2 và Mị ổ ọ ườ ặ ơ ượ ổ th = const
M
ω
M
th
P =1
P =2
III. Cách d ng đ c tính t nhiên và bi n tr ự ặ ự ế ở
1.Cách d ng đ c tính c t nhiên ự ặ ơ ự
Vì đ c tính c t nhiên c a đ ng c KĐB là nh ng đ ng cong ph c t p nên mu n d ng ta c n ph iặ ơ ự ủ ộ ơ ữ ườ ứ ạ ố ự ầ ả
xác đ nh nhi u đi m [M,s] . Có th s d ng m t trong hai cách sau đây :ị ề ể ể ử ụ ộ
a. Cách d ng chính xác ự
- Khi bi t đ y đ các thông s c a đ ng c nh :ế ầ ủ ố ủ ộ ơ ư
Pđm , Uđm , I2đm , E2đm , r1 ,x1 , r2 , x2 , ho c ặ
' '
2 2 .
, , ,
th nm
M Mkd
dm dm
M M
r x M M
λ λ
= =
T các thông s đó ta s xác đi nh đ c sừ ố ẽ ị ượ th , Mth ,
1
'
2
r
ar
=
và thay chúng vào bi u th c tính mô men . Cho để ứ ộ
tr t s bi n thiên t 0 -1 ta s có các giá tr c a mô men t ng ng . T các giá tr [M,s] thu đ c ti nượ ế ừ ẽ ị ủ ươ ứ ừ ị ượ ế
hành d ng đ ng đ c tính ự ườ ặ
+ N u không bi t các thông s ế ế ố
, '
1 2 1 2 2 2
, , , , ,
nm dm
r r x x E I
thì có th xác đ nh các thông s sể ị ố th , Mth , a nh sau :ư
5