Đề cương ôn tập cuối HK2 lớp 10 – HBT Trang 1/7
TRƯỜNG THPT HAI BÀ TRƯNG
TỔ TOÁN
ĐỀ CƯƠNG ÔN TẬP CUỐI HKII NĂM HỌC 2022 – 2023
MÔN TOÁN – KHỐI 10
Họ và tên: ……………………………………... Lớp: …………….
I. PHẦN TRẮC NGHIỆM
HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
Câu 1. Điểm nào sau đây thuộc đồ thị hàm số
1
1
y
x
A.
3
2;0 .
M B.
4
2; 1 .
M
C.
1
2;1 .
M D. 2
1
2; .
3
M
Câu 2. Tìm tập xác định của hàm số
1
4
x
yx x .
A.
4; \ 0 .
D  B.
D  C.
4; \ 0;1 .
D D.
\ 0 .
D
Câu 3. Đồ thị nào sau đây là parabol có đỉnh
1;0
I?
A. 2
1.
y x x
B. 2
2 1.
y x x
C. 2
2 3.
y x x
D. 2
2 1.
y x x
Câu 4. Trục đối xứng của parabol
2
: 2 6 3P y x x
là
A.
3.
x
B.
3.
y
C.
3.
2
x
D.
3.
2
y
Câu 5. Hàm số 2
2 4 1y x x
đồng biến trên khoảng nào?
A.
; 1 .
B.
1; .
C.
1; .
D.
;1 .

Câu 6. Cho parabol
2
: , 0
P y ax bx c a có đồ thị hình vẽ. Trong các mệnh đề dưới đây mệnh đề nào
sai?
A. Hàm số nghịch biến trên khoảng
1;1 .
B. Hàm số đồng biến trên khoảng
1; .
C. Hàm số nghịch biến trên khoảng
;1 .
 D. Hàm số đồng biến trên khoảng
4;3 .
Câu 7. Giá trị nhỏ nhất của hàm số 2
6 1y x x
là:
A.
8.
B.
3.
C.
1.
D.
10.
Câu 8. Xác định hàm số bậc hai 2
6
y ax bx
có đồ thị đi qua hai điểm
1;1 , 2;2
A B .
A. 2
2 5 6.
y x x
B. 2
3 3 6.
y x x
C. 2
3 10 6.
y x x
D. 2
2 8 6.
y x x
Câu 9.Tìm tập nghiệm của phương trình
2
3 1 2
x x x
.
A.
{3;1}.
S
B.
{3}.
S
C.
{3;6}.
S
D.
{1}.
S
Câu 10. Tìm tập nghiệm của phương trình
2
2 4 9 3x x x
.
A.
.
B.
{0}.
C.
2;0 .
D.
2 .
Đề cương ôn tập cuối HK2 lớp 10 – HBT Trang 2/7
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Câu 11. Trong mặt phẳng toạ độ Oxy,tìm một vectơ chỉ phương của đường thẳng
d
:
2 3
3
x t
y
.
A.
3;0 .
u
B.
2; 3 .
u
C.
3; 3 .
u
D.
0;1 .
u
Câu 12. Trong mặt phẳng toạ độ Oxy, vectơ nào sau đây là một vectơ pháp tuyến của
:3 5 0?
d x y
A.
3; 1 .
n
B.
1;3 .
n
C.
1;3 .
n
D.
3;1 .
n
Câu 13. Trong mặt phẳng toạ độ Oxy, cho đường thẳng
: 2 3 1 0.
d x y
Tìm một vectơ chỉ phương của
d
.
A.
(1; 3).
x
B.
( 3;1).
e
C.
(3;2).
n
D.
(2; 3).
v
Câu 14. Trong mặt phẳng toạ độ Oxy, tìm một vectơ chỉ phương của dường thẳng đi qua
3; 1
C
và
1;5
D.
A.
3
3;1 .
u
B.
4
3;1 .
u
C.
1
1; 3 .
u
D.
2
1;3 .
u
Câu 15. Trong mặt phẳng Oxy, vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua
2;3
A và
4;1 ?
B
A.
; .1 1
n
B.
1; 2 .
n
C.
2; 1 .
n
D.
;
.2 2
n
Câu 16. Phương trình tham số của đường thẳng
d
đi qua
6
(
3; )
A
và có vectơ chỉ phương 4
)2
(
;
u
là
A.
1 2 .
2
x t
y t
B.
6 4 .
3 2
x t
y t
C.
3 2 .
6
x t
y t
D.
2 4 .
1 2
x t
y t
Câu 17. Trong mặt phẳng toạ độ Oxy, viết phương trình tham số của đường thẳng đi qua
1;1
A và
2;2
B.
A. 1
.
1 2
x t
y t
B. 1
.
2 2
x t
y t
C.
2 2 .
1
x t
y t
D.
.
x t
y t
Câu 18. Trong mặt phẳng toạ độ Oxy, điểm nào dưới đây nằm trên đường thẳng
: 2 1 0?
x y
A.
(1; 3).
A
B.
( 1; 3).
B
C.
(1;2).
C D.
(1; 2).
D
Câu 19. Trong mặt phẳng toạ độ Oxy, viết phương trình tổng quát của đường thẳng
d
qua
1;1
M và song
song với đường thẳng
': 1 0
d x y
.
A.
1 0.
x y
B.
0.
x y
C.
1 0.
x y
D.
2 0.
x y
Câu 20. Trong mặt phẳng toạ độ Oxy, viết phương trình tổng quát của đường thẳng
d
đi qua điểm
1;0
M
và vuông góc với đường thẳng
: .
2
x t
y t
A.
2 2 0.
x y
B.
2 2 0.
x y

C.
2 1 0.
x y
D.
2 1 0.
x y
Câu 21. Trong mặt phẳng toạ độ Oxy, viết phương trình tổng quát của đường thẳng
d
đi qua
1; 1
A
và
vuông góc với đường thẳng
: 2 1 0
x y
.
A.
2 1 0.
x y
B.
2 3 0.
x y
C.
2 3 0.
x y
D.
2 5 0.
x y
Câu 22. Trong mặt phẳng toạ độ Oxy, viết phương trình đường thẳng đi qua hai điểm
(2;0)
A và
(0;3)
B.
A.
1.
3 2
x y
B.
0.
3 2
x y
C.
1.
2 3
x y
D.
1.
2 3
x y
Câu 23. Trong mặt phẳng toạ độ
Oxy
, cho tam giác
ABC
có
(2; 5)
A,
(4;1)
B và
(2;3)
C. Viết phương trình
tham số của đường trung tuyến kẻ từ đỉnh
A
của tam giác
ABC
.
A. 3
.
2 7
x t
y t
B.
3 7 .
2
x t
y t
C.
3 7 .
2
x t
y t
D. 3
.
2 7
x t
y t
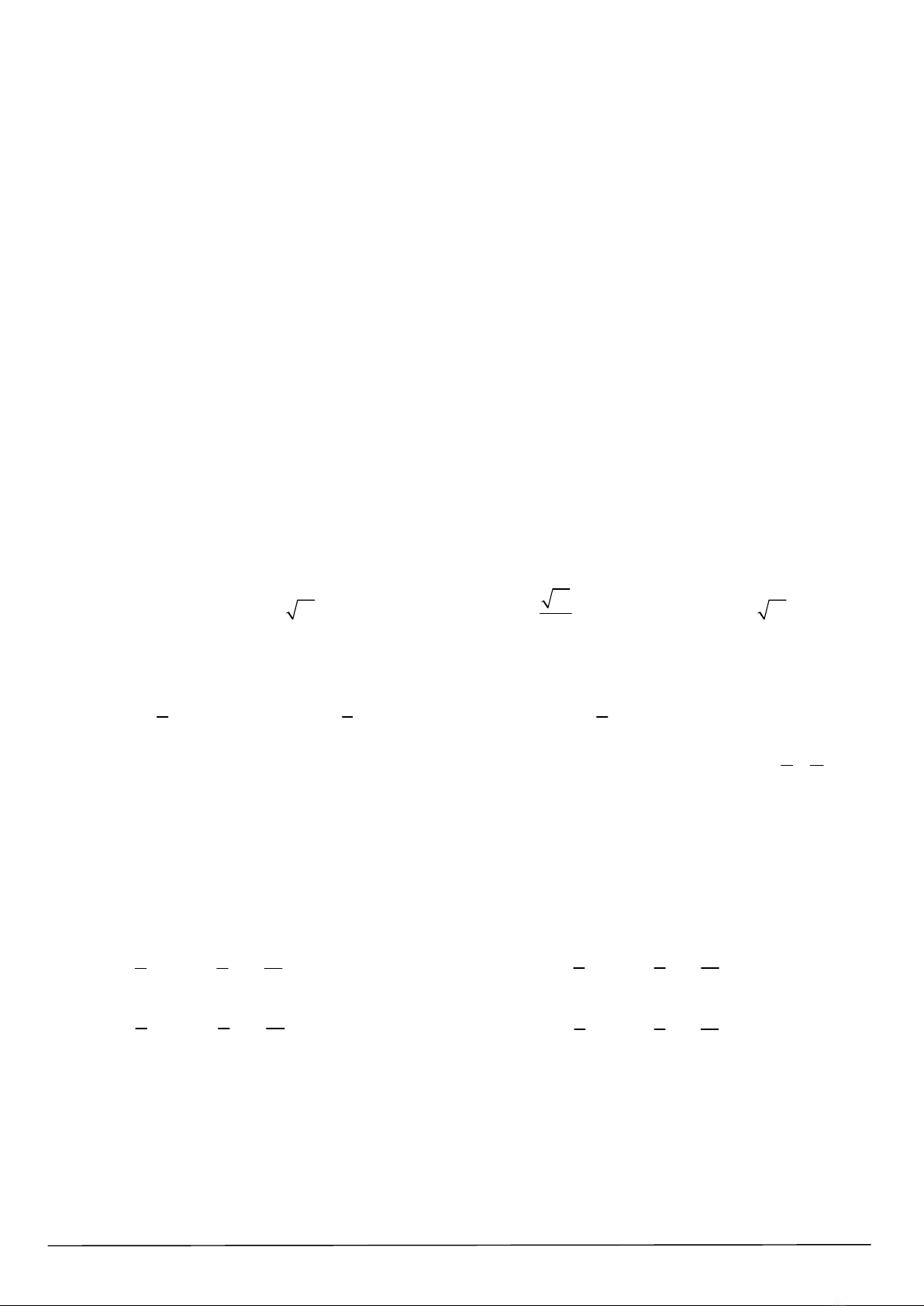
Đề cương ôn tập cuối HK2 lớp 10 – HBT Trang 3/7
Câu 24. Trong mặt phẳng toạ độ
Oxy
, cho hình bình hành
ABCD
có đỉnh
–2;1
A và phương trình đường
thẳng chứa cạnh
CD
là
1 4
3
x t
y t
. Viết phương trình tham số của đường thẳng chứa cạnh
AB
.
A.
2 3 .
2 2
x t
y t
B.
2 4 .
1 3
x t
y t
C.
2 3 .
1 4
x t
y t
D.
2 3 .
1 4
x t
y t
Câu 25. Trong mặt phẳng toạ độ
Oxy
, viết phương trình tham số của đường thẳng
d
đi qua điểm
4; 7
M
và song song với trục
.Ox
A.
1 4 .
7
x t
y t
B. 4
.
7
x
y t
C. 7
.
4
x t
y
D.
.
7
x t
y
Câu 26. Trong mặt phẳng toạ độ
Oxy
, tìm vị trí tương đối của hai đường thẳng 1
: 7 2 1 0
x y
và
2
4
:
1 5
x t
y t
.
A. vuông góc với nhau. B. cắt nhau nhưng không vuông góc nhau.
C. song song. D. trùng nhau.
Câu 27. Trong mặt phẳng toạ độ
Oxy
, cho 1
2 2
:
1 3
x t
d
y t
và 2
1 3
:
1 2
x t
d
y t
. Tính số đo góc giữa hai đường
thẳng
1
d
và
2
d
.
A.
0
45 .
B.
0
60 .
C.
0
90 .
D.
0
30 .
Câu 28. Trong mặt phẳng toạ độ
Oxy
, tính khoảng cách từ điểm
5; 2
M
đến đường thẳng
: 3 2 6 0.
x y
A.
13.
B.
13.
C.
13 .
13
D.
2 13.
Câu 29. Trong mặt phẳng toạ độ
Oxy
, gọi
là góc giữa hai đường thẳng 1
: 4 2 1 0
d x y
và
2
: 2 2 0.
d x y
Tính
cos .
A.
2
cos .
5
B.
3
cos .
5
C.
4
cos .
5
D.
cos 1.
Câu 30. Trong mặt phẳng toạ độ
Oxy
, xét vị trí tương đối của hai đường thẳng sau:
1
: 1
3 4
x y
d
và
2
:3 4 10 0
d x y
.
A. Trùng nhau. B. Song song.
C. Cắt nhau nhưng không vuông góc nhau. D. Vuông góc với nhau.
Câu 31. Trong mặt phẳng
Oxy
, lập phương trình đường tròn đi qua hai điểm
3;0 , 0;2
A B và có tâm
thuộc đường thẳng
: 0
d x y
.
A.
2 2
1 1 13.
2 2 2
x y
B.
2 2
1 1 13.
2 2 2
x y
C.
2 2
1 1 13.
2 2 2
x y
D.
2 2
1 1 13.
2 2 2
x y
Câu 32. Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
1;2
A,
5;2
B,
1; 3
C
có phương trình là:
A. 2 2
25 19 49 0.
x y x y
B. 2 2
2 6 3 0.
x y x y
C. 2 2
6 1 0.
x y x y
D. 2 2
6 1 0.
x y x xy
Câu 33. Tìm tọa độ tâm
I
và tính bán kính
R
của đường tròn
2 2
( ) : 2 5 9
C x y
.
A.
( 2;5), 81.
I R
B.
(2; 5), 9.
I R
C.
(2; 5), 3.
I R
D.
( 2;5), 3.
I R
Đề cương ôn tập cuối HK2 lớp 10 – HBT Trang 4/7
Câu 34. Đường tròn
2 2
: 2 4 3 0
C x y x y
có tâm
I
, bán kính
R
là
A.
1;2 , 2.
I R B.
1;2 , 2 2.
I R C.
1; 2 , 2 2.
I R D.
1; 2 , 2.
I R
Câu 35. Phương trình nào sau đây là phương trình của một đường tròn?
A. 2 2
4 2 8 3 0.
x y xy x y
B. 2 2
2 4 5 1 0.
x y x y
C. 2 2
14 2 2018 0.
x y x y
D. 2 2
4 5 2 0.
x y x y
Câu 36. Trong mặt phẳng tọa độ
Oxy
, cho điểm
1;1
I và đường thẳng
:3 4 2 0
d x y
. Đường tròn
tâm
I
và tiếp xúc với đường thẳng
d
có phương trình
A.
2 2
1 1 5.
x y
B.
2 2
1 1 25.
x y
C.
2 2
1 1 1.
x y
D.
2 2
1
1 1 .
5
x y
Câu 37. Cho đường tròn
2 2
: 2 4 4 0
C x y x y
và điểm
1;5
A. Đường thẳng nào trong các đường
thẳng dưới đây là tiếp tuyến của đường tròn
C
tại điểm
A
.
A.
5 0.
y
B.
5 0.
y
C.
5 0.
x y
D.
5 0.
x y
Câu 38. Viết phương trình tiếp tuyến của đường tròn 2 2
( ) : ( 2) ( 4) 25
C x y
, biết tiếp tuyến vuông góc
với đường thẳng
: 3 4 5 0
d x y
.
A.
4 3 29 0.
x y
B.
4 3 29 0
x y
hoặc
4 3 21 0.
x y
C.
4 3 5 0
x y
hoặc
4 3 45 0.
x y
D.
4 3 5 0
x y
hoặc
4 3 3 0.
x y
Câu 39. Tìm các tiêu điểm của Elip
2 2
1.
9 1
x y
A.
1
3;0 ;
F
2
0; 3 .
F
B.
1
8;0 ;
F
2
0; 8 .
F
C.
1
3;0 ;
F
2
0; 3 .
F
D.
1
8;0 ;
F
2
8;0 .
F
Câu 40. Phương trình chính tắc của elip
E
có độ dài trục lớn gấp
2
lần độ dài trục nhỏ và đi qua điểm
2; 2
A
là
A.
2 2
1.
24 16
x y
B.
2 2
1.
36 9
x y
C.
2 2
1.
16 4
x y
D.
2 2
1.
20 5
x y
Câu 41. Cho của hypebol
2 2
: 1
16 5
x y
H
. Hiệu các khoảng cách từ mỗi điểm nằm trên
H
đến hai tiêu
điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
8.
B.
16.
C.
4.
D.
5.
Câu 42. Tọa độ các tiêu điểm của hypebol
2 2
: 1
16 9
x y
H
là
A.
1 2
5;0 ; 5;0 .
F F B.
1 2
0; 5 ; 0;5 .
F F
C.
1 2
0; 7 ; 0; 7 .
F F D.
1 2
7;0 ; 7;0 .
F F
Câu 43. Cho parabol
2
6
:
1
P y
x
. Tính khoảng cách từ tiêu điểm đến đường chuẩn của parabol?
A.
8.
B.
16.
C.
4.
D.
2.
Đề cương ôn tập cuối HK2 lớp 10 – HBT Trang 5/7
ĐẠI SỐ TỔ HỢP
Câu 44. Có bao nhiêu cách chọn một học sinh từ một nhóm gồm
5
học sinh nam và
6
học sinh nữ?
A.
5
. B.
30
. C.
6
. D.
11
.
Câu 45. Một đội văn nghệ có
10
người gồm
6
học sinh nam và
4
học sinh nữ. Cần chọn ra một học sinh
nam và một học sinh nữ để hát song ca. Hỏi có bao nhiêu cách chọn?
A.
24
. B.
10
. C.
12
. D.
20
.
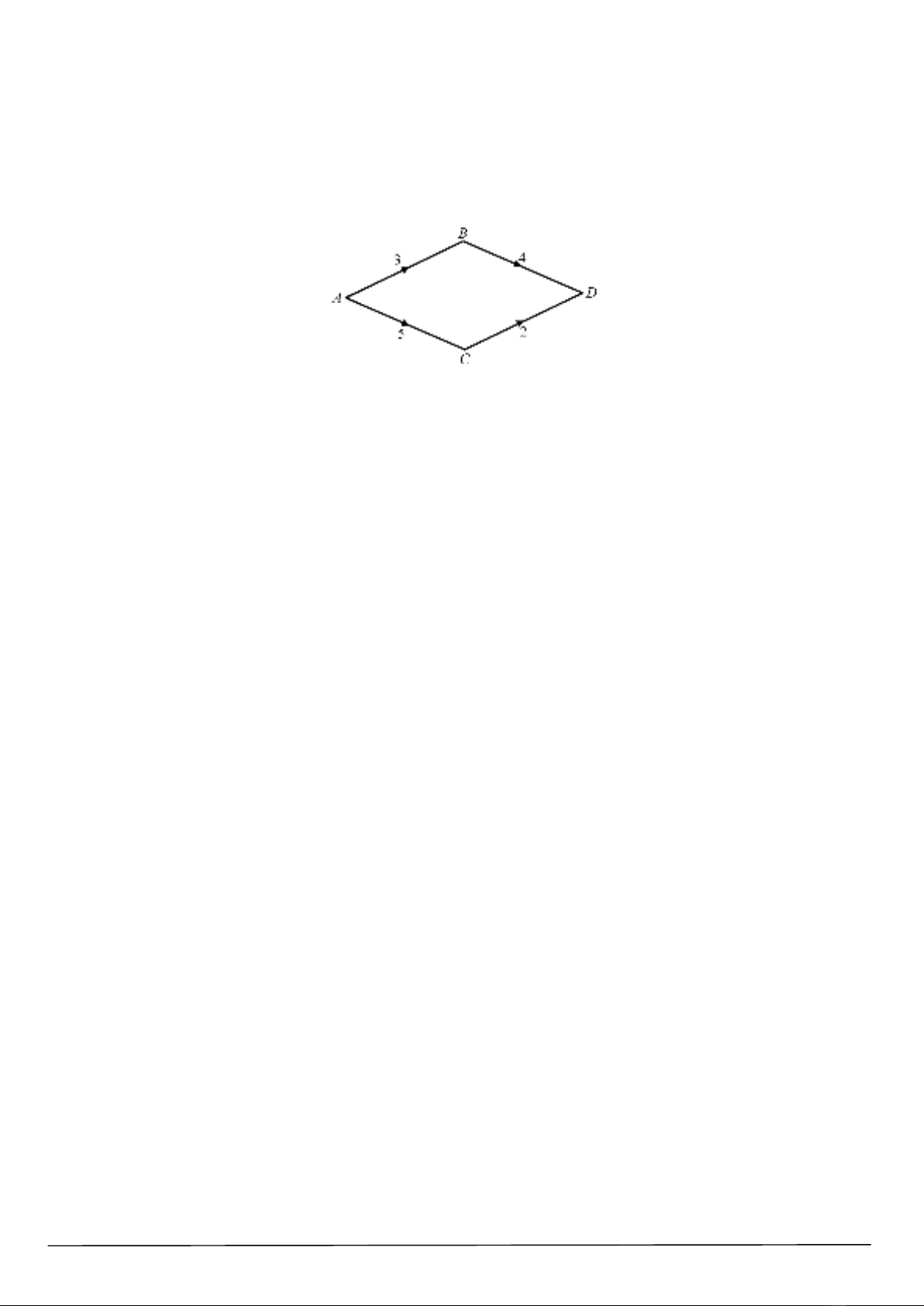
Câu 46. Xét mạng đường nối các tỉnh
, , , A B C D
(như hình vẽ), trong đó số viết trên mỗi cạnh cho biết số
con đường nối hai tỉnh nằm ở hai đầu mút của cạnh. Hỏi có bao nhiêu cách đi từ tỉnh
A
đến tỉnh
D
?
A.
14
. B.
22
. C.
120
. D.
49
.
Câu 47. Có bao nhiêu số tự nhiên có hai chữ số được tạo thành từ các chữ số
1;3;5;7;9
?
A.
12
. B.
90
. C.
25
. D.
20
.
Câu 48. Với các chữ số
0,1,2,3,4,5,6
có thể lập được bao nhiêu số tự nhiên có
5
chữ số khác nhau?
A.
1270
. B.
1250
. C.
2160
. D.
1260
.
Câu 49. Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
A. 36. B. 62. C. 54. D. 42.
Câu 50. Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau?
A. 156. B. 144. C. 96. D. 134.
Câu 51. Từ các số
1, 2,3, 4,5,6,7
lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số chia hết
cho 5.
A. 360. B. 120. C. 480. D. 347.
Câu 52. Gọi
S
là tập hợp
21
số nguyên dương đầu tiên. Có bao nhiêu cách chọn hai số từ tập
S
để tổng của
chúng là một số lẻ?
A.
100
. B.
210
. C.
110
. D.
105
.
Câu 53. Một hộp chứa
19
tấm thẻ được đánh số từ
1
đến
19
. Có bao nhiêu cách lấy lần lượt 2 tấm thẻ từ hộp
đó sao cho tích của hai số ghi trên hai tấm thẻ là một số chẵn?
A.
36
. B.
135
. C.
162
. D.
45
.
Câu 54. Một cái hộp chứa
6
viên bi đỏ và
4
viên bi xanh. Có bao nhiêu cách lấy lần lượt
2
viên bi từ hộp
đó sao cho viên bi được lấy lần thứ hai là viên bi xanh?
A.
36
. B.
40
. C.
24
. D.
90
.
Câu 55. Trên kệ sách có
6
quyển sách Toán khác nhau,
7
quyển sách Văn khác nhau và
8
quyển sách Tiếng
Anh khác nhau. Hỏi có bao nhiêu cách lấy
2
quyển sách thuộc
2
môn khác nhau?
A.
146
. B.
336
. C.
420
. D.
210
.
Câu 56. Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có bao nhiêu cách chọn 3
bông hoa có đủ cả 3 màu.
A. 240. B. 210. C. 18. D. 120.
Câu 57. Có bao nhiêu cách xếp 5 bạn A, B, C, D, E vào một ghế dài gồm 5 chỗ?
A.
5
5 .
B.
4!.
C.
5!.
D.
5.
Câu 58.Có bao nhiêu cách xếp 5 bạn A, B, C, D, E vào một ghế dài gồm 5 chỗ sao cho C ngồi chính giữa?
A.
2!.2!.
B.
4!.
C.
5!.
D.
5.
Câu 59. Có bao nhiêu cách xếp 5 bạn A, B, C, D, E vào một ghế dài gồm 10 chỗ?
A.
5
10
.C
B.
5
10
.A
C.
5!.
D.
5.
Câu 60. Có bao nhiêu cách bầu ban chấp hành lớp gồm 3 người: lớp trưởng, lớp phó và ủy viên trong một
lớp có 35 học sinh?
A.
3
35
.A
B.
3
35
.C
C.
3!.
D.
32
35
.A
Câu 61. Từ các chữ số
1,2,3, 4
có thể tạo thành bao nhiêu số tự nhiên gồm 6 chữ số trong đó chữ số 1 xuất
hiện 3 lần các chữ số còn lại xuất hiện 1 lần.
A.
60.
B.
360.
C.
720.
D.
120.