S GD & ĐT VĨNH PHÚCỞ
TR NG THPT NGUY N VI T XUÂNƯỜ Ễ Ế
MÃ Đ: 106Ề
(Đ thi g m 5 trang)ề ồ
Đ THI KH O SÁT CH T L NG L N 4Ề Ả Ấ ƯỢ Ầ
Năm h c: 2017-2018ọ
Môn: Toán 11
Th i gian làm bài: 90 phút; ờ
(Không k th i gian giao đ)ể ờ ề
H , tên thí sinh:..........................................................................ọ
S báo danh:...............................................................................ố
Câu 1: Cho đa giac lôi (H) co 22 canh. Goi X la tâp h p cac tam giac co ba đinh la ba đinh cua ơ (H). Chon
ngâu nhiên 2 tam giac trong X, tinh xac suât đê chon đc 1 tam giac co 1 canh la canh cua đa giac ươ (H)
va 1 tam giac không co canh nao la canh cua đa giac (H).
A.
749
1995
.B.
7
816
.C.
748
1995
.D.
3
17
.
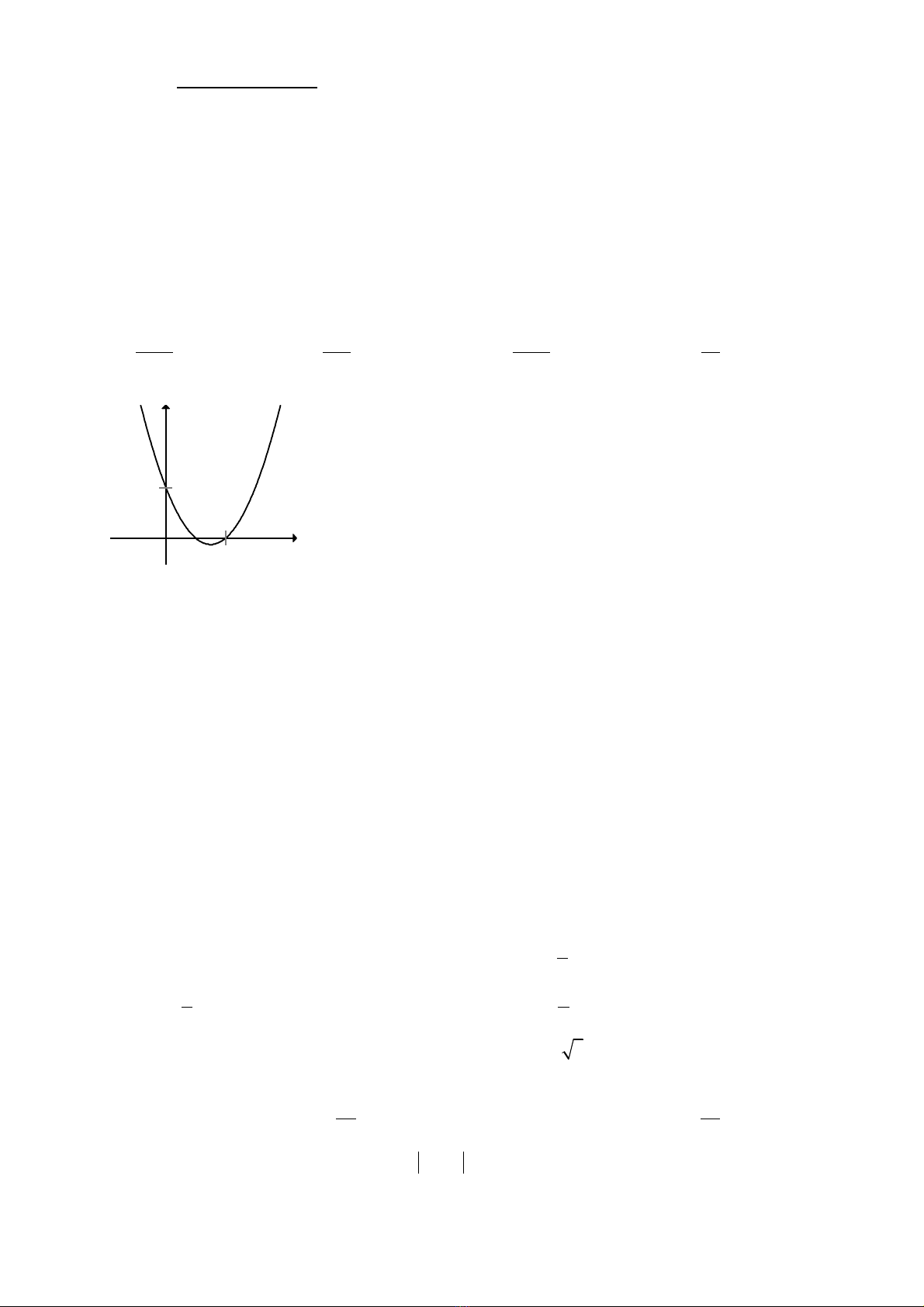
Câu 2: Đ th hình bên d i là đ th c a hàm s nào?ồ ị ướ ồ ị ủ ố
x
y
O
1
A.
2
3 1.y x x
= − + −
B.
2
2 3 1.y x x
= − +
C.
2
2 3 1.y x x
= − + −
D.
2
3 1.y x x
= − +
Câu 3: Cho đng th ng ườ ẳ d có ph ng trình: ươ
, t a đ vect ch ph ng c a đng th ng ọ ộ ơ ỉ ươ ủ ườ ẳ d
là:
A. (-1;1) B. (1;3) C. (1;-4) D. (2;-1)
Câu 4: Đo hàm c a hàm s ạ ủ ố
2
cos( 1)y x= +
b ng:ằ
A.
2
sin( 1).y x= - +
B.
2
2 in( 1).y xs x= - +
C.
2
sin( 1).y x= +
D.
2
2 sin( 1).y x x= +
Câu 5: Trong m t ph ng ặ ẳ
Oxy
cho hai đi m ể
( ) ( )
1; 3 , 2;5A B
− −
. Vi t ph ng trình t ng quát c aế ươ ổ ủ
đng th ng đi qua hai đi m ườ ẳ ể
, .A B
A.
8 3 1 0x y
+ + =
.B.
3 8 30 0x y
− + − =
.C.
8 3 1 0x y
+ − =
.D.
3 8 30 0x y
− + + =
.
Câu 6: Cho hình t di n ứ ệ ABCD có tr ng tâm ọG. M nh đ nào sau đây là ệ ề sai?
A.
0
+ + + =
uuur uuur uuur uuur
GA GB GC GD
.
B.
( )
1.
4
= + + +
uuur uuur uuur uuur uuur
OG OA OB OC OD
C.
( )
1.
4
= + +
uuur uuur uuur uuur
AG AB AC AD
D.
( )
2.
3
= + +
uuur uuur uuur uuur
AG AB AC AD
Câu 7: Cho tam giác
ABC
vuông t i ạ
A
có
, 3AB a AC a
= =
và
AM
là trung tuy n. Tính tích vôế
h ng ướ
. ?BA AM
uuuruuuur
A.
2
a
B.
2
2
a
−
C.
2
a
−
D.
2
2
a
Câu 8: T p nghi m c a b t ph ng trình ậ ệ ủ ấ ươ
2x 1 1
−
là
A.
(
] [
)
0 1;
− +�� �
.B.
[ ]
S 0;1
=
.C.
( )
S 0;1
=
.D.
{ }
S 0;1
=
.
Trang 1/6 - Mã đ thi 106ề
Câu 9: Cho
, ,n k k n<�N
. Trong các công th c sau đây công th c nào ứ ứ sai?
A.
!
!
k
n
n
Ak
=
B.
!
n
P n=
C.
k n k
n n
C C
-
=
D.
( )
!
! !
k
n
n
Ck n k
=-
Câu 10: Bi t r ng ế ằ
( )
2
lim 5 2 5 5
x
x x x a b
-
+ + = +
v i ớ
, .a b ?
Tính
5 .S a b= +
A.
1.S=
B.
5.S= -
C.
5.S=
D.
1.S= -
Câu 11: M t ch t đi m chuy n đng có ph ng trình ộ ấ ể ể ộ ươ
3 2
3 9 2,S t t t
= − − +
trong đó t đc tính b ngượ ằ
giây và S đc tính b ng mét. Gia t c t i th i đi m v n t c b tri t tiêu là:ượ ằ ố ạ ờ ể ậ ố ị ệ
A.
2
12 / .m s
B.
2
9 / .m s
C.
2
9 / .m s
−
D.
2
12 / .m s
−
Câu 12: Cho c p s c ng ấ ố ộ
( )
n
u
bi t ế
5
18u
=
và
2
4 .
n n
S S=
Tìm s h ng đu tiên ố ạ ầ
1
u
và công sai
d
c aủ
c p s c ng.ấ ố ộ
A.
1
2, 4u d= =
.B.
12, 3u d= =
.C.
1
2, 2u d
= =
.D.
13, 2u d= =
.
Câu 13: Cho ph ng trình ươ
( )
2
1 3 1 0m x x− + − =
. Ph ng trình có nghi m khi ?ươ ệ
A.
5
4
m
−
B.
5
4
m
=
C.
1m
=
D.
5
4
m
−
.
Câu 14: Cho t di n ứ ệ ABCD bi t ế
AB AC CD a
= = =
. Trên đo n ạAC l y đi m ấ ể M sao cho
( )
0AM x a x
= < <
. M t ặ
( )
α
đi qua M song song v i ớAB và CD l n l t c t ầ ượ ắ BC, BD, AD t i ạN,P,Q.
Gi s ả ử
AB CD
⊥
, tìm
x
đ di n tích t giácể ệ ứ MNPQ là l n nh t.ớ ấ
A.
2
a
x=
B.
3
4
a
x
=
C.
3
2
a
x
=
D.
3
4
a
x
=
Câu 15: Gi i b t ph ng trình ả ấ ươ
3
3 2 3 3 1,x x x x
− + + + −
(v i ớx
R
), ta đc t p nghi m làượ ậ ệ
;
a
S c
b
� �
� �
=� �
� �
v i ớ
*
, , ,a b c ?
phân s ố
a
b
t i gi n. Khi đó ố ả
abc+ +
b ng:ằ
A. 5. B. 7. C. 6. D. 9.
Câu 16: Ph ng trình: ươ
2
sin 0
3 3
x
π
� �
− =
� �
� �
có nghi m là:ệ
A.
3
2 2
k
x
π π
= +
.B.
x k
π
=
.C.
3
x k
ππ
= +
.D.
5 3
2 2
k
x
π π
= +
.
Câu 17: T ng các nghi m c a ph ng trình: ổ ệ ủ ươ
1 2
14 14 14
2
n n n
C C C
+ +
= +
là
A. 16 B. 12 C. 15 D. 13
Câu 18: Gi iả ph ng trình ươ
+ =sin cos 2x x
.
A.
( )
ππ
= +
5.
4
x k k Z
B.
( )
ππ
= +
.
4
x k k Z
C.
( )
ππ
= +
2 .
4
x k k Z
D.
( )
ππ
= +
.
4
x k k Z
Câu 19: G i ọ
S
là t p nghi m c a b t ph ng trình ậ ệ ủ ấ ươ
2
2
31.
4
x x
x
+ -
-
Khi đó
( )
2; 2S-�
là t p nào sauậ
đây?
A.
( )
2; 1 .- -
B.
.
C.
( ]
2; 1 .- -
D.
( )
1; 2 .-
Câu 20: Tìm s h ng đu và công b i c a CSN ố ạ ầ ộ ủ
( )
n
u
, bi t: ế
− =
− =
4 2
5 3
72
144
u u
u u
.
A.
1
12, 2u q
= =
.B.
1
12, 2u q= − = −
.C.
1
12, 2u q
= = −
.D.
1
12, 2u q= − =
.
Trang 2/6 - Mã đ thi 106ề
Câu 21: Trong m t ph ng v i h t a đặ ẳ ớ ệ ọ ộ
Oxy
. Tìm t a đ đi m ọ ộ ể
M
là nh c a đi m ả ủ ể
( )
2;1M
qua phép
đi x ng tâm ố ứ
( )
3; 2I
−
.
A.
( )
1;5M
.B.
( )
4; 5M
−
.C.
( )
1; 3M
−
D.
( )
5; 4M
−
.
Câu 22: Cho dãy s ố
( )
n
u
xác đnh b i:ị ở
1
1
3
u
=
và
1
1.
3
n n
n
u u
n
+
+
=
. T ng ổ
3 10
2
1
...
2 3 10
u u
u
S u
= + + + +
b ng.ằ
A.
25942
59049
B.
29524
59049
C.
3280
6561
D.
1
243
Câu 23: Cho hàm số
( )
2
5 14 9f x x x
= − + −
. T p h p các giá tr c a ậ ợ ị ủ
x
đ: ể
( )
' 0f x
<
là:
A.
7
1; .
5
� �
� �
� �
B.
7
; .
5
� �
−
� �
� �
C.
7; .
5
� �
+
� �
� �
D.
7 9
; .
5 5
� �
� �
� �
Câu 24: Cho h ph ng trình ệ ươ
2 2
2
2 8 3 12 9
4 18 6 7 2 3 1 0
+ + = + +
+ + − + − + =
x xy x y y
x y x x y
có nghi m là (a;b). Khi đó giá trệ ị
bi u th c ể ứ
2 2
T 5a 4b
= +
A.
T 21
=
.B.
T 5
=
.C.
T 24
=
.D.
T 4
=
.
Câu 25: T đ cao 55,8 mét c a tháp nghiêng Pisa n c Italia ng i ta th m t qu bóng cao su ch mừ ộ ủ ướ ườ ả ộ ả ạ
xu ng đt. Gi s m i l n ch m đt qu bóng l i n y lên đ cao b ng ố ấ ả ử ỗ ầ ạ ấ ả ạ ả ộ ằ
1
10
đ cao mà qu bóng đtộ ả ạ
tr c đó. Tính đ dài hành trình c a qu bóng đc th t lúc ban đu cho đn khi nó n m yên trênướ ộ ủ ả ượ ả ừ ầ ế ằ
m t đt.ặ ấ
A.
62 m
B.
61,38m
C.
68, 2 m
D.
50, 22m
Câu 26: Hàm s ố
4 9
1
yx x
= + -
v i ớ
0 1,x< <
đt giá tr nh nh t t i ạ ị ỏ ấ ạ
,
a
xb
=
(
,a b
nguyên d ng,ươ
phân s ố
a
b
t i gi n). Khi đó ố ả
a b+
b ng.ằ
A. 141. B. 4. C. 139. D. 7.
Câu 27: Nghi m l n nh t c a ph ng trình ệ ớ ấ ủ ươ
sin 3 cos 0x x
− =
thu c đo n ộ ạ
3
;
2 2
� �
π π
−
� �
� �
là:
A.
.
π
B.
4.
3
π
C.
5.
4
π
D.
3.
2
π
Câu 28: Phát bi u nào sau đây là ểsai?
A.
lim (
n n
u c u c
= =
là h ng s ).ằ ố B.
( )
lim 0 1
n
q q
= >
.
C.
1
lim 0
n
=
.
D.
( )
1
lim 0 1
k
k
n
= >
Câu 29: Trong m t ph ng v i h tr c ặ ẳ ớ ệ ụ
,Oxy
cho hình vuông
ABCD
có tâm là đi m ể
.I
G i ọ
( )
1; 2G-
và
( )
3;1K
l n l t là tr ng tâm các tam giác ầ ượ ọ
ACD
và
ABI
. Bi t ế
( )
;A a b
v i ớ
0.b>
Khi đó
2 2
a b+
b ng:ằ
A. 37. B. 3. C. 5. D.
9.
Trang 3/6 - Mã đ thi 106ề
Câu 30: Cho đng th ng ườ ẳ
( )
: 1d y x= +
và Parabol
( )
2
: 2.P y x x= - -
Bi t r ng ế ằ
( )
d
c t ắ
( )
P
t i haiạ
đi m phân bi t ể ệ
, .A B
Khi đó
A B
x x+
b ng:ằ
A. 2. B.
5.
2
C.
3.
2
D. 4.
Câu 31: Tìm t t c các giá tr c a m đ hàm s ấ ả ị ủ ể ố
( )
1 1 khi 0
1 khi 0
1
x x x
x
f x x
m x
x
− − + <
=−
+
+
liên t c t i ụ ạ
0.x
=
A.
1m
=
.B.
2m
= −
.C.
1m
= −
.D.
0m
=
Câu 32: Giá tr c a tham s ị ủ ố
m
đ ph ng trình ể ươ
sin 2 2 sin 2
4
x x m
π
� �
+ + − =
� �
� �
có đúng hai nghi mệ
thu c kho ng ộ ả
3
0; 4
π
� �
� �
� �
là:
A.
( )
1; 2 1
− −
B.
2
2; 2
� �
−
� �
� �
� �
C.
1 1
;
2 2
� �
−

� �
.D.
2; 2
2
� �
−

� �
.
Câu 33: Ph ng trình ti p tuy n c a đ th hàm s ươ ế ế ủ ồ ị ố
3 2
3 4y x x x= - +
t i đi m có hoành đ ạ ể ộ
1x=
là
gì?
A.
1.y x= +
B.
1.y x= -
C.
2 1.y x= +
D.
3 2.y x= -
Câu 34: Trong m t ph ng ặ ẳ
Oxy
cho đng th ng ườ ẳ
d
có ph ng trình ươ
2 0x y
+ − =
. Vi t ph ng trìnhế ươ
đng th ng ườ ẳ
d
là nh c a ả ủ
d
qua phép đng d ng có đc b ng cách th c hi n liên ti p phép v tồ ạ ượ ằ ự ệ ế ị ự
tâm
( )
1; 1I
− −
t s ỉ ố
1
2
k
=
và phép quay tâm
O
góc
45
−
A.
y x
= −
B.
0y
=
C.
y x
=
D.
0x
=
Câu 35: S nghi m c a ph ng trình ố ệ ủ ươ
3 2 2 1x x
− = −
là
A. 2B. 0C. 1D. 3
Câu 36: Cho đ th hàm s ồ ị ố
( )
1
: ;
=
C y x
đi m M có hoành đ ể ộ
2 3
= −
M
x
thu c ộ(C). Bi t ti p tuy nế ế ế
c a ủ(C) t i M l n l t c t ạ ầ ượ ắ Ox, Oy t iạ
A
,.
B
. Tính di n tích tam giácệ
OAB
.
A.
1
OAB
S
∆
=
.B.
4
OAB
S
∆
=
.C.
2
OAB
S
∆
=
.D.
2 3
OAB
S
∆
= +
.
Câu 37: Cho t di n ứ ệ
.S ABC
có 2 m t ặ
( )
ABC
và
( )
SBC
là 2 tam giác đu c nh ề ạ
a
.
3
2
a
SA
=
.
M
là
đi m trên ể
AB
sao cho
( )
0AM b b a
= < <
.
( )
P
là m t ph ng qua ặ ẳ
M
và vuông góc v i BC. Tính thi tớ ế
di n c a ệ ủ
( )
P
và t di n ứ ệ
.S ABC
có di n tích b ng.ệ ằ
A.
( )
2
3 3
4
a b
−
B.
( )
2
3
4
a b−
C.
( )
2
3 3
16
a b−
D.
( )
2
3 3
8
a b
−
Câu 38: Cho đng th ng ườ ẳ
( )
d
có ph ng trình ươ
4 3 5 0x y
+ − =
và đng th ng ườ ẳ
( )
∆
có ph ng trìnhươ
2 5 0x y
+ − =
. Ph ng trình đng th ng ươ ườ ẳ
( )
d
là nh c a đng th ng ả ủ ườ ẳ
( )
d
qua phép đi x ng tr cố ứ ụ
( )
∆
là
A.
3 0x
− =
B.
3 1 0x y
+ − =
C.
3 2 5 0x y
+ − =
D.
3 0y
− =
Câu 39: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. G i ọM, N l n l t là trung đi m c aầ ượ ể ủ
AD và BC. Giao tuy n c a (ế ủ SMN) và (SAC) là:
A. SG (G là trung đi m ểAB). B. SO
C. SF (F là trung đi m ểCD). D. SD.
Trang 4/6 - Mã đ thi 106ề
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy l n ớ
.AB
G i ọM là trung đi m c aể ủ
.SC
Giao đi m c a ể ủ BC v i m t ph ng ớ ặ ẳ
( )
ADM
là:
A. giao đi m c a ể ủ BC và AM.B. giao đi m c a ể ủ BC và
SD
.
C. giao đi m c a ể ủ BC và
AD
.D. giao đi m c a ể ủ BC và DM.
Câu 41: Cho
( 3;1)b
−
r
và
( 4; 2).c
− −
r
Tính tích vô h ng ướ
.b c
rr
?
A. 14 B. -10 C. 10 D. 12
Câu 42: Cho hình chóp S.ABCD có đáy là hình bình hành. G i ọG là tr ng tâm c a tam giác ọ ủ ABC và N là
đi m th a mãn ể ỏ
2SN NA
=
uuur uuur
. Kh ng đnh nào sau đây là đúng.ẳ ị
A.
( )
/ /GN SBC
B.
/ /GN SD
C.
/ /SN CD
D.
( )
/ /GN SCD
Câu 43: Tìm
5 3
5 2
8 2 1
lim .
4 2 1
n n
In n
− +
=+ +
A.
8I
=
.B.
4I
=
.C.
1I
=
.D.
2I
=
.
Câu 44: Cho
, ,a b c
là các đng th ng trong không gian, m nh đ nào sau đây là đúng?ườ ẳ ệ ề
A. Cho
/ /a b
. M i m t ph ngọ ặ ẳ
( )
α
ch a ứ
c
trong đó
c a
⊥
và
c b⊥
thì đu vuông góc v i m t ề ớ ặ
ph ng ẳ
( )
,a b
.
B. Cho
a b
⊥
n m trong m t ph ngằ ặ ẳ
( )
α
, m i m t ph ngọ ặ ẳ
( )
β
ch a ứ
a
và vuông góc v i ớ
b
thì
( ) ( )
α β
⊥
C. Cho
a b
⊥
.M i m t ph ng ch a ọ ặ ẳ ứ
b
đu vuông góc v i ề ớ
a
.
D. Cho
a b
⊥
và m t ph ngặ ẳ
( )
α
ch a ứ
a
, m t ph ngặ ẳ
( )
β
ch a ứ
b
thì
( ) ( )
α β
⊥
Câu 45: Cho hình chóp
S.ABCD
có đáy
ABCD
là hình vuông c nh ạ
a
,
SA a 3=
và vuông góc v iớ
đáy. Góc gi a đng th ng ữ ườ ẳ
SD
và m t ph ng ặ ẳ
(ABCD)
b ngằ
A.
o
60
.B.
o
45
.C.
o
30
.
D.
3
acr sin 5
.
Câu 46: Cho hình chóp đu ềS.ABCD có đáy ABCD là hình vuông tâm O, c nh b ng ạ ằ
2 , 2 .a SA a=
Côsin c a góc gi a ủ ữ
( )
SDC
và
( )
SA C
b ng:ằ
A.
21 .
14
B.
21 .
3
C.
21 .
2
D.
21 .
7
Câu 47: Cho hình chóp
.S ABCD
có đáy là hình vuông c nh ạ
3
,2
=
a
a SD
. Hình chi u vuông góc c aế ủ
đi m ể
S
trên m t ph ng đáy là trung đi m c a c nh ặ ẳ ể ủ ạ
AB
. Tính kho ng cách t đi m ả ừ ể
A
đn m tế ặ
ph ng ẳ
( )
?SBD
A.
3.
4
=a
d
B.
2.
3
=
a
d
C.
3.
5
=a
d
D.
3.
2
=a
d
Câu 48: T các ch s 2, 3, 4 l p đc bao nhiêu s t nhiêu s t nhiên có 9 ch s , trong đó ch sừ ữ ố ậ ượ ố ự ố ự ữ ố ữ ố
2 có m t 2 l n, ch s 3 có m t 3 l n, ch s 4 có m t 4 l n?ặ ầ ữ ố ặ ầ ữ ố ặ ầ
A. 1260. B. 120. C. 1728. D. 40320.
Câu 49: Cho
( )
1; 2a
= −
r
. V i giá tr nào c a ớ ị ủ y thì
( )
3;b y
= −
r
vuông góc v i ớ
a
r
:
A. 6B. –6 C. 3D. –
3
2
.
Câu 50: Cho
( )f x
là đa th c th a mãn ứ ỏ
( )
3
15
lim 12
3
x
f x
x
−=
−
. Tính
( )
3
2
3
5 11 4
lim 6
x
f x
Tx x
− −
=− −
A.
3
20
T=
.B.
3
40
T=
.C.
1
4
T=
D.
1
20
T=
.
Trang 5/6 - Mã đ thi 106ề