Đ i h c Bách Khoa TPHCMạ ọ Đ KI M TRA GI A KỲ 1. Năm h c 2010-2011Ề Ể Ữ ọ
Khoa Đi n – Đi n Tệ ệ ử Môn: C s ơ ở t đ ngự ộ
B môn ĐKTĐộNgày thi: 02/11/2010
---o0o--- Th i gian làm bài:ờ 60 phút
(Sinh viên không đ c phép s d ng tài li u in ho cượ ử ụ ệ ặ
photo)
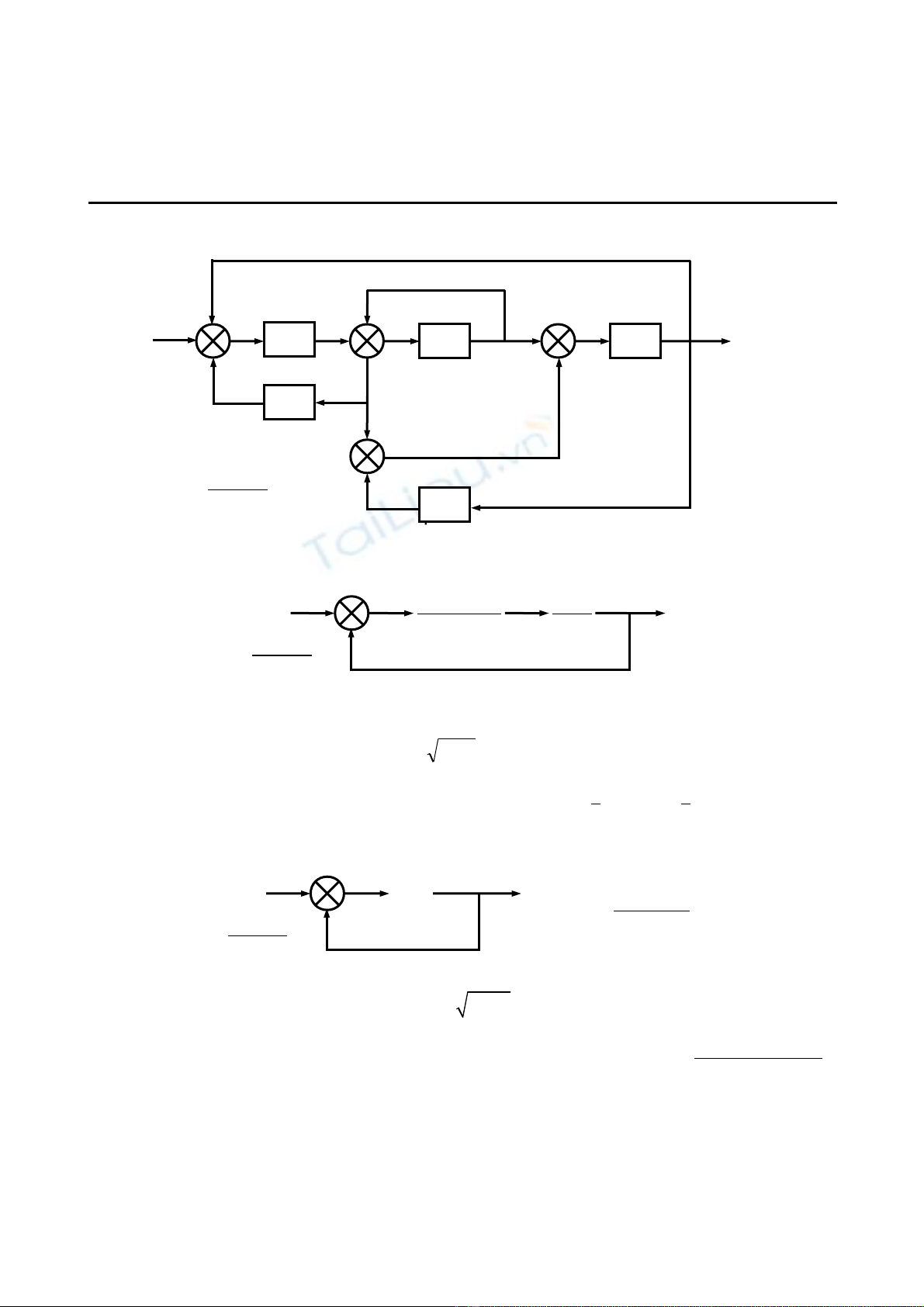
Bài 1: (2.0 đi m) Tính hàm truy n t ng đ ng c a h th ng có s đ kh i hình 1ể ề ươ ươ ủ ệ ố ơ ồ ố ở
Bài 2: (2.0 đi m) Ch n 1 trong 2 câu 2A ho c 2Bể ọ ặ
2A. Vi t ph ng trình tr ng thái mô t h kín hình 2 v i hai bi n tr ng thái ế ươ ạ ả ệ ở ớ ế ạ x1(t) và x2(t) cho
trên s đ , bi n ơ ồ ế x3(t) t ch n.ự ọ
2B. Cho hê thông phi tuyên bâc 2 nh sau v i ư ớ u(t) la tin hiêu đâu vao, y(t) la tin hiêu đâu ra.
)()(2)(
)(2)()()()(
)()()()(
1
2212
2211
tutxty
tutxtxtxtx
txtxtxtx
+=
+−=
−=
Viêt ph ng trinh biên trang thai tuyên tinh hoa tai điêm lam viêc ươ
1,]41[ == u
T
x
.
Bài 3: (3.0 đi m) Cho h th ng hình 3.ể ệ ố ở
3.1 V QĐNS c a h th ng khi ẽ ủ ệ ố
+ ∞<≤ K0
. Tìm đi u ki n c a ề ệ ủ K đ h th ng n đ nh.ể ệ ố ổ ị
3.2 Tìm c c thu c QĐNS có d ng ự ộ ạ
2
1s j
ξω ω ξ
= − + −
v i ớ
=0.5
ξ
, tìm K lúc đó.
Bài 4: (3.0 đi m) ểCho h th ng h i ti p âm đ n v có hàm truy n h là ệ ố ồ ế ơ ị ề ở
22
1.0
)10(
)4.0(200
)( +
+
=−
ss
es
sG
s
4.1 V bi u đ Bode biên đ và pha c a ẽ ể ồ ộ ủ G(s).
4.2. Đánh giá tính n đ nh c a h kínổ ị ủ ệ
4.3. D a vào đ c tính t n s c a ự ặ ầ ố ủ G(s), b n hãy cho nh n xét v đ v t l , th i gian quá đ và saiạ ậ ề ộ ọ ố ờ ộ
s xác l p khi tín hi u vào làm n c đ n v .ố ậ ệ ấ ơ ị
(H t)ế
CNBM
r(t)y(t)
+_
Hìn h 2
5
2
+
s
32
1
2
++
ss
x1
x2
R(s)Y(s)
+_
Hìn h 3
)(sG
)9(
)(25
)(
2
+
+
=
ss
Ks
sG
G1(s)
R(s)Y(s)
Hìn h 1
G2(s)
+
_G3(s)G4(s)
G5(s)
_
_
+
+
++
+
Gi iả
Câu 1.
Đ ng ti n: ườ ế
Vòng kín:
1 1 2 2 3 3 4 5 4 1 3 4 5 1 4
; ; ; ;L G G L G L G G L G G G L G G= − = − = = − = −
Đ nh th c chính: ị ứ
( )
1 2 3 4 5 1 3 2 3
1 2 3 4 5 1 3 4 1 4 1 2 4 5 3 4 5
1
1
L L L L L L L L L
G G G G G G G G G G G G G G G G G
∆ = − + + + + + +
= + + − + + − −
Đ nh th c con: ị ứ
1 2
1; 1∆ = ∆ =
Hàm truy n t ng đ ng: ề ươ ươ
( ) ( )
( )
1 1 2 2
1 3 4 1 4
1 2 3 4 5 3 4 5 1 2 4 5 1 3 4 1 4
1
td
C s
G s R s
P P
G G G G G
G G G G G G G G G G G G G G G G G
=
∆ + ∆
=∆+
=+ + − − − + +
Ho c bi n đ i t ng đ ng s đ kh i (cách này nhanh h n).ặ ế ổ ươ ươ ơ ồ ố ơ
Câu 2A.
T s đ , ta có:ừ ơ ồ
( ) ( ) ( ) ( ) ( )
1 2 1 1 2
25 2
5
X s X s x t x t x t
s
= ⇒ = − +
+
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2 1 2 2 2 1
2
12 3
2 3
X s R s X s x t x t x t r t x t
s s
= − ⇒ + + = −
+ + 
Đ t : ặ
( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
2 2 2 3
3 2 3 3 2 1
2 3
x t x t x t x t
x t x t x t x t x t x t r t
= =
⇒
= = − − − +
K t h p v i PTVP xế ợ ớ 1(t), ta có: PTTT
( ) ( ) ( )
( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( )
( )
( )
( )
( )
( )
( ) ( )
( )
[ ]
( )
( )
( )
1 1 2
2 3
3 3 2 1
1
1 1
2 2
3 2
1
2
2
5 2
2 3
5 2 0 0
0 0 1 0
1 3 2 1
1 0 0
x t x t x t
x t x t
x t x t x t x t r t
y t x t
x t x t
x t x t r t
x t x t
x t
y t x t
x t
= − +
=
= − − − +
=
−
= +
− − −
⇒
=
Câu 2B.
1 1 2 2
2 1 2 2
1
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) 2 ( )
( ) 2 ( ) ( )
f t x t x t x t
f t x t x t x t u t
h t x t u t
= −
= − +
= +
( )
( )
( )
[ ]
( )
1 1
2 1
1 2
1
2
1 2 1
2,1
4
2 2 ,
1
,
2 1 2 ,
,
( ) ( ) 1 4 0
( ) 3
( ) 1 2
2 ( ) 4
0, 2 0 , 1
2
x u
x u
x u
x u
f f x t x t
x x x t
Ax t
f f x t
x x
f
h h h
u
B C D
f x x u
u
÷
÷
÷
∂ ∂
−
∂ ∂
= = = −
−
∂ ∂
∂ ∂
∂
∂ ∂ ∂
∂
= = = = = =
∂ ∂ ∂ ∂
∂
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
( )
( )
( ) ( )
( )
[ ]
( )
( ) ( )
1
1 1
1 1
2
22 2
1
2
2 3
4 0
10
3
22
44
:
12 0
3
y x u
x t x t
x t x t u t
x t
x tx t x t PTTT
u t u t x t
y t u t
y t y t x t
= + =
= −
= +
−
= −
⇒
= −
= +
= −
% %
%%
%
%
%
%%
% %
%%
Câu 3.
PTĐT:
( ) ( )
( ) ( )
3 2
2
25
1 0 1 0 9 25 25 0 1
9
s K
G s s s s K
s s
+
+ = ⇔ + = ⇔ + + + =
+
( )
3 2
25
1 1 0
9 25
Ks s s
⇔ + =
+ +
Zero : không có
Pole :
1 2,3
9 19
0, 4.50 2.18
2 2
p p i i= = − ± − ±;
Ti m c n: ệ ậ
1 2 3
3
3
3
3
p p p
OA
π
α π
π
+ +
= = −
=
−
Đi m tách nh p: ể ậ
( )
3 2
21
2
9 25
125
6
3 2.18
3 18 25 3
0
25 6
3 3.82
3
s s s
K
s
K s s
ss
+ +
⇒ = −
= − + −
∂ + +
⇒ = − = ⇔
∂= − − −
;
;
(c 2 đ u thu c QĐNS).ả ề ộ
Giao đi m QĐNS v i tr c o: áp d ng tiêu chu n n đ nh Routh cho PTĐT (1).ể ớ ụ ả ụ ẩ ổ ị
s31 25 ĐK n đ nhổ ị
s29 25K
s125-(25K/9) K<9
s025K K>0
V y đi u ki n h th ng n đ nh: 0 < K < 9.ậ ề ệ ệ ố ổ ị
Ta có: Kgh = 9. Thay vào (1) gi i ra ta đ c: sả ượ 1 = -9, s2 = 5i, s3 = -5i
V y giao đi m QĐNS v i tr c o: sậ ể ớ ụ ả 2 = 5i, s3 = -5i
Góc xu t phát t i c c ph c pấ ạ ự ứ 2:
( )
( )
0
2 1 2 3
0
0 0 0 0
180 arg arg
9 19 9 19 9 19
180 arg 0 arg
2 2 2 2 2 2
180 154 90 64
p p p p
i i i
θ
= − − − −
= − − + − − − + − − −
÷ ÷ ÷
÷ ÷ ÷
= − − = −
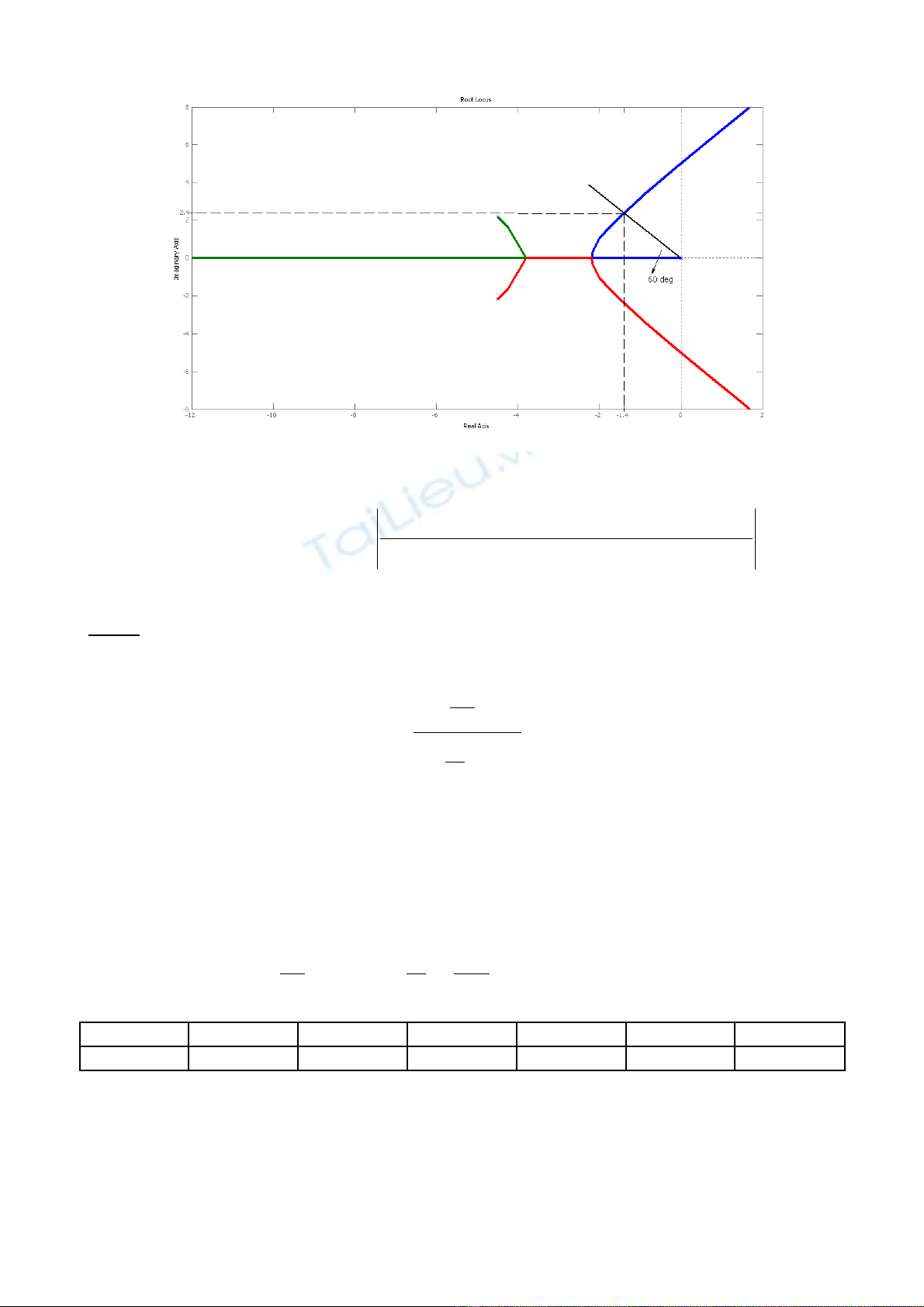
3.2
T QĐNS, ta suy ra: c c c n tìm: ừ ự ầ
1.4 2.4s i= − +
Thay vào PTĐT, ta tính đ c K: ượ
( ) ( ) ( )
3 2
1.4 2.4 9 1.4 2.4 25 1.4 2.4 1.91
25
i i i
K− + + − + + − +
= =
Câu 4.
4.1
Vi t l i hàm truy n vòng h : ế ạ ề ở
( )
0.1
2
2
1
0.8 1
0.4
11
10
s
s
G s e
s s
−
+
÷
=
+
÷
Các t n s c t: ầ ố ắ
( ) ( )
1 2
0.4 / , 10 /rad s rad s
ω ω
= =
Đi m đ u: ể ầ
( )
( ) ( )
0
0
0.1
:20log 0.8 2* 20log 0.1 38
AL dB
ω
ω
=
= − =
Tính bode pha:
( )
0
0
180
180 arctan 2arctan 0.1
0.4 10
ω ω
ϕ ω ω
π
= − + − −
÷ ÷
ω (rad/s) 0.1 0.4 1 2 4 10
ϕ(ω) (0)-168 -142 -129 -135 -162 -240
Bi u đ Bode nh sau:ể ồ ư