ONTHIONLINE.NET
SỞ GIÁO DỤC & ĐÀO TẠO ĐĂKLĂK
Trường THPT Trần Quốc Toản
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2008 - 2009
MÔN: TOÁN 11
(Thời gian :90 phút)
I.Phần chung cho cả hai ban:
Bài 1:( 2 điểm ) Giải các phương trình sau:
a. 2
2cos 2 -3cos2 1 0
x x
b.(
3
+ 1)sin2x - 2sinx cosx - (
3
- 1) cos2x = 1
Bài 2: ( 2 điểm ) Có 14 người gồm 8 nam và 6 nữ, chọn ngẫu nhiên một tổ 6 người. Tính:
a. Số cách chọn để được một tổ có nhiều nhất là 2 nữ.
b. Xác suất để được một tổ chỉ có 1 nữ.
Bài 3 : ( 2 điểm ) Trong mặt phẳng Oxy ,cho vectơ
2;3v
, đường thẳng d : x + y – 2 = 0 và
đường tròn (C) có phương trình : (x – 2)2 + ( y – 4 )2 = 16 .
a. Viết phương trình đường thẳng d’ là ảnh của d qua phép V
T.
b. Viết phương trình đường tròn (C’) là ảnh của (C) qua phép
1
0;
2
V
Bài 4 :( 2 điểm ) Cho hình chóp S.ABCD có đáy là hình thang , đáy lớn là AD và AD = 2BC.
Gọi O là giao điểm của AC và BD , G là trọng tâm của tam giác SCD.
a. Chứng minh rằng : OG // (SBC).
b. Mặt phẳng (P) đi qua O và song song với AD và SB .Tìm thiết diện của hình chóp với
mặt phẳng (P) .
II. Phần riêng :
A . Dành cho ban KHTN
Bài 5: (2 điểm )
a. Biết tổng các hệ số trong khai triển ( 1 + 2x )n bằng 6561.
Tìm hệ số của số hạng chứa
x
.
b.Tam giác ABC thoả mãn : sin2A + sin2B = 4sinAsinB .
Chứng minh rằng :Tam giác ABC vuông.
B . Dành cho ban cơ bản
Bài 6: ( 2 điểm )
a.Tìm hệ số của x8 trong khai triển
15
1
2
2
x
.
b. Một cấp số cộng có năm số hạng mà tổng của số hạng đầu và số hạng thứ ba bằng 28,
tổng của số hạng thứ ba và số hạng cuối bằng 40 .Hãy tìm cấp số cộng đó .
--------------------------------------------HẾT----------------------------------------------
ĐÁP ÁN
Bài 1:( 2 điểm ) Giải các phương trình sau:
a. 2
2cos 2 -3cos2 1 0
x x
Ta có *) cos 2x = 1
x = k
, k
Z . (0,5 điểm)
**) cos 2x =
1
2
x =
6
+ k
, k
Z (0,5 điểm)
b.(
3
+ 1)sin2x - 2sinx.cosx - (
3
- 1) cos2x = 1 (1)
Xét *) cosx = 0
(1) :
3
+ 1 = 1
PTVN.
**)cosx
0
(1) :
3
sin2x - 2sinx.cosx -
3
cos2x = 0
3
tan2x – 2tanx -
3
= 0 . (0,5 điểm)
Suy ra i) tanx =
3
x = ,
3
k k Z
.
ii) tanx = 1,
6
3
x k k Z
. (0,5 điểm)
Bài 2: ( 2 điểm )
a. Số cách chọn để được một tổ có nhiều nhất là 2 nữ.
*) TH1: 0 nữ + 6 nam, số cách chọn là
0 6
6 8
C C
.
**) TH2: 1 nữ + 5 nam, số cách chọn là
1 5
6 8
C C
. (0,5 điểm)
***) TH3: 2 nữ + 4 nam, số cách chọn là
2 4
6 8
C C
.
Cả 3 trường hợp, số cách chọn là 0 6 1 5 2 4
6 8 6 8 6 8
1414
C C C C C C . (0,5 điểm)
b. Xác suất để được một tổ chỉ có 1 nữ.
6
1 4
1 5
6 8
3 0 0 3
336
336 16
3003 143
* ) .
* * ) ä i A l µ b iÕ n c è : " C h ä n ® î c 6 n g ê i t
r o n g
® ã c h Ø c ã 1 n ÷ " , . .
* * * ) .
n C
G
n A C C
n A
P A
n
(1 điểm)
Bài 3 : ( 2 điểm )
a. Lấy M(0;2) thuộc d.
'4;3
'dMMTv
Vì d // d’ nên pt d’ có dạng :x+y +C =0 (C khác -2). (0,5 điểm)
7043''
CCdM
Vậy pt d’ là: x+y-7=0 . (0,5 điểm)
b. Đường tròn (C ) có tâm I(2 ;4) , R=4.
1;2I'IV
2
1
O;
và R’= 2. (0,5 điểm)
PT (C’) là: ( x -1 )2 + ( y – 2)2 = 4. (0,5 điểm)
Bài 4 :( 2 điểm )
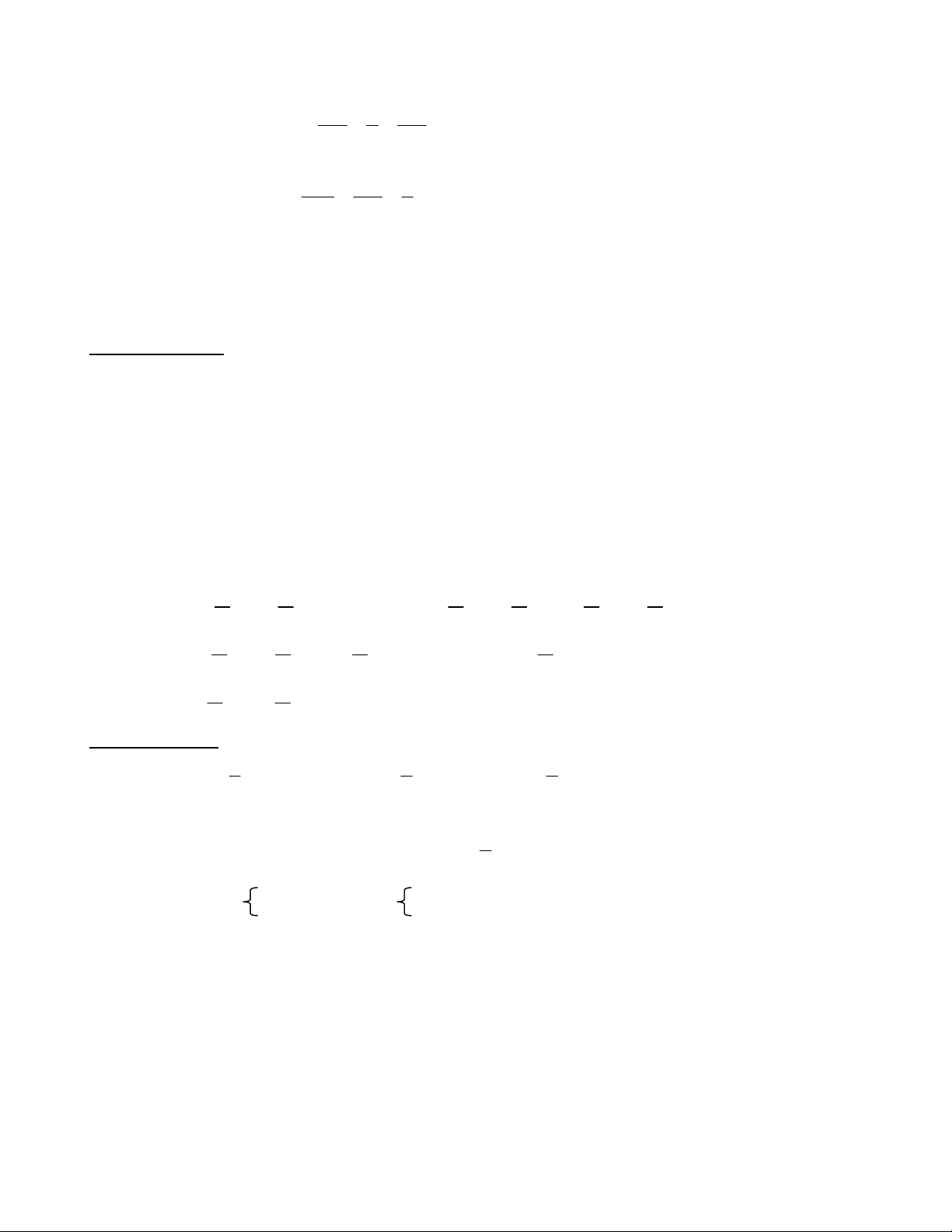
a.Chứng minh rằng : OG // (SBC).
*) Từ AD = 2 BC
2
3
BC OD
AD DB
. (0,5 điểm)
Xét tam giác :DMB có
2
3
MD OD
MG OB
OG //MB.
**) MB
(SBC)
OG // (SBC) . (0,5 điểm)
b. Vì (P) //AD , O
(P) *) Dựng KQ đi qua O và KQ //AD
**) Từ K dựng KH // SB. (0,5 điểm)
***)Từ H dựng HR // AD.
Vậy thiết diện là hình thang : KQRH. (0,5 điểm)
Bài 5: ( 2 điểm )
a.Ta có : *)
0 0
(1 2 ) 1 (2 ) 2
n n
n k n k k k k k
n n
k k
x C x C x
.
**) Mặt khác
0
2
n
k k
n
k
C
= (1 + 2 )n = 6561 = 3 8
n = 8. (0,5 điểm)
***) Số hạng chứa x4
k = 4 .
****) Hệ số của số hạng chứa x4 : 4 4
8
2 1120
C. (0,5 điểm)
b. sin2A + sin2B = 4sinAsinB .
2 sin (A+B) cos(A-B) = 2[cos(A-B) – cos(A+B)].
( Cos
2
C
- sin
2
C
) [ cos(A – B) (Cos
2
C
- sin
2
C
) - Cos
2
C
- sin
2
C
] = 0. (0,5 điểm)
- ( Cos
2
C
- sin
2
C
) ( Cos
2
C
[1 – cos(A – B)] + sin
2
C
[ 1 + cos(A –B) ] ) = 0
Cos
2
C
= sin
2
C
C = 900. (0,5 điểm)
Bài 6: (2 điểm )
a.Ta có : *)
15 15
15 15 15 15
15 15
0 0
1 1 1
(2 ) (2 ) ( ) 2 ( )
2 2 2
k k k k k k k
k k
x C x C x
.
**) Số hạng chứa x8 : 15 – k = 8
k = 7. (0,5 điểm)
***) Hệ số của số hạng chứa x8 :
7 15 7 7 7
15 15
1
2 ( ) 2
2
C C
. (0,5 điểm)
b. Theo giả thiết : 1 3
3 5
28
40
u u
u u
1
11
3
u
d
(0,5 điểm)
Vậy cấp số cộng : 11 ; 14 ; 17 ; 20 ; 23 . (0,5 điểm)