ĐỀ SỐ 5
Câu 1. Tính diện tích
S
của hình phẳng được giới hạn bởi đồ thị hàm số
221y x x= + −
và đường
thẳng
23yx=+
.
A.
32
3
S=
. B.
49
3
S=
. C.
22
3
S=
. D.
11
3
S=
.
Câu 2. Cho hình phẳng
D
giới hạn bởi đồ thị
2
( ): 3P y x x=−
và trục
Ox
. Tính thể tích khối tròn
xoay sinh ra khi cho hình
D
quay quanh trục
Ox
.
A.
64
15
V
=
. B.
92
V
=
. C.
81
4
V
=
. D.
81
10
V
=
.
Câu 3. Cho số phức
z
thõa
z.z 1=
và
z 1 2−=
. Tính tổng phần thực và phần ảo của
z
.
A.
2
. B.
1
. C.
1−
. D.
0
.
Câu 4. Tính
2
e
1
1 lnx
I dx
x
+
=
A.
3 2 2
I2
+
=
. B.
4 2 2
I2
−
=
. C.
3 3 2
I3
+
=
. D.
6 3 2
I3
−
=
.
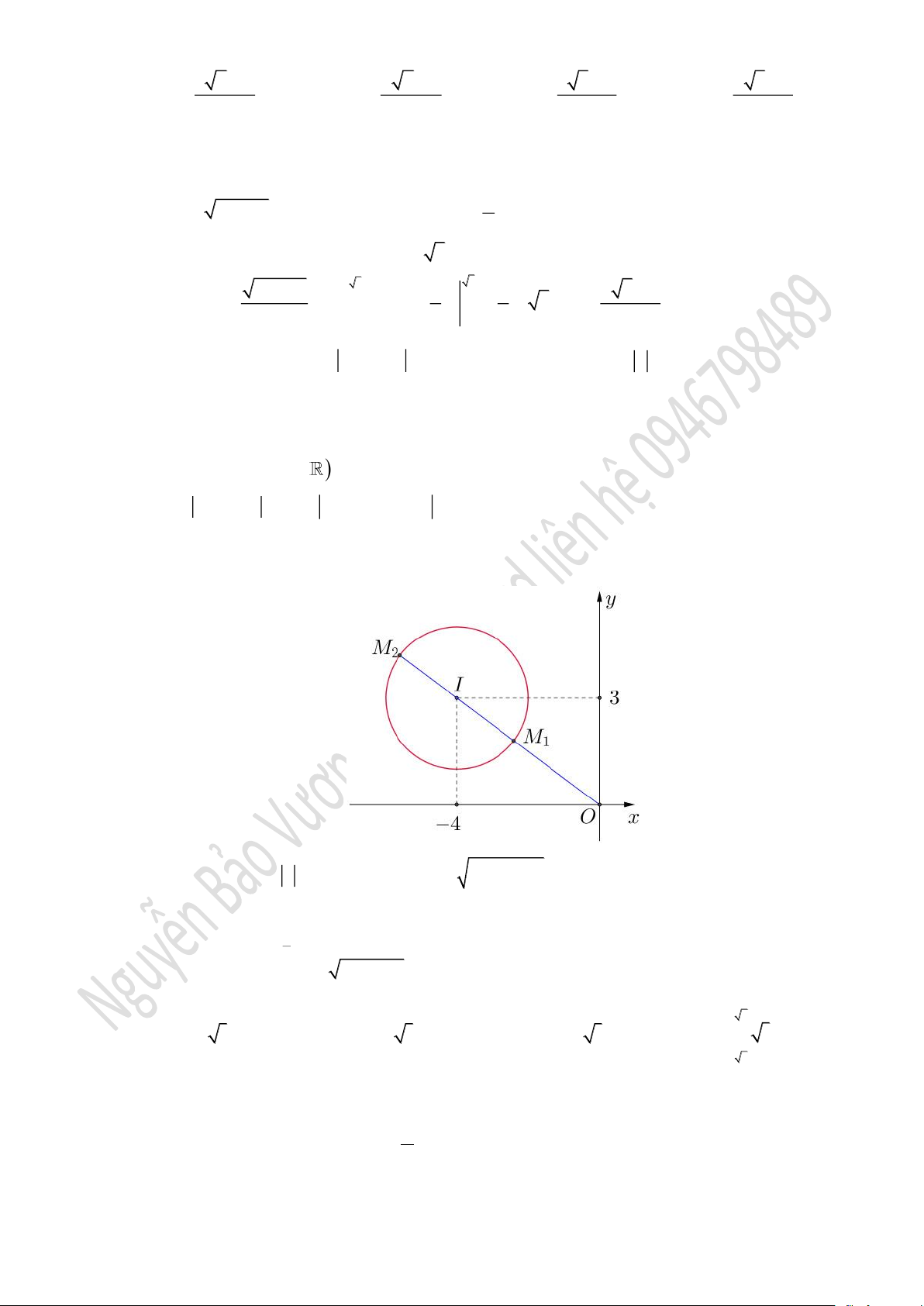
Câu 5. Cho số phức
z
thỏa mãn
3 4 2zi− + =
. Tìm giá trị nhỏ nhất của
z
A.
2
. B.
1
. C.
3
. D.
5
.
Câu 6. Cho tích phân
2
0
sin 6 cosI x xdx
=+
, đặt
6 costx=+
ta có
A.
6
7
I tdt=
. B.
7
6
I tdt=
. C.
7
6
2.I tdt=
. D.
7
6
I tdt=
.
Câu 7. Cho
4
1
41
ln dx
ea
e
xx b
+
=
, với
,ab
là các số nguyên. Khi đó đẳng thức nào đúng?
A.
30ab+=
. B.
ab=
. C.
120ab =
. D.
10ab−=
.
Câu 8. Cho
4
0
cos2 dxx x b
a
=+
, trong đó
a
,
b
. Tìm khẳng định đúng?
A.
1
2
ab =
. B.
2ab =−
. C.
1
2
ab =−
. D.
2ab =
.
Câu 9. Cho
3ln5lnd
12
2ln
0
bax
ee
Ix
x−=
+
=
với
,ab
. Tìm khẳng định Đúng.
A.
ba 0
. B.
10 a
. C.
1
22 =+ba
. D.
02 − ba
.
Câu 10. Trong các số phức
z
thỏa mãn
iziz −−=− 23
. Tìm phần thực của số phức
z
sao cho
z
nhỏ
nhất.
A.
5
1
. B.
5
2
−
. C.
5
1
. D.
5
2
.