ĐỀ SỐ 8.
ZALO 0946798489 ĐỀ BÀI
Câu 1: Cho hàm số
32
1
x
yx
+
=+
, đồ thị hàm số tiếp xúc với đồ thị hàm số
y x m=+
khi
A.
2m=
hoặc
6m=
. B.
2m=
hoặc
4m=
.
C.
2m=−
hoặc
4m=−
. D.
1m=
hoặc
5m=
.
Câu 2: Cho hàm số
11 10 9 7
11 5 9
x x x
y= − + +
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
( )
;0−
và nghịch biến trên
( )
0;+
.
B. Hàm số nghịch biến trên
( )
0;1
và đồng biến trên
( )
0;+
.
C. Hàm số nghịch biến trên .
D. Hàm số đồng biến trên .
Câu 3: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2cos sin 1y x x= − +
.
Khi đó
.Mm
bằng
A.
0
. B.
25
4
. C.
25
8
. D.
2
.
Câu 4: Cho hàm số
42
21y x x= − + +
. Mệnh đề nào sau đây đúng?
A. Giá trị cực tiểu của hàm số là 0. B. Hàm số đạt cực đại tại điểm
0x=
.
C. Hàm số đạt cực tiểu tại các điểm
1x=
. D. Giá trị cực đại của hàm số là 2.
Câu 5: Cho hàm số
32
32y x x= + +
có đồ thị
( )
C
. Phương trình tiếp tuyến của
( )
C
có hệ số góc nhỏ
nhất là
A.
31yx= − +
. B.
34yx= − +
. C.
31yx=−
. D.
0y=
.
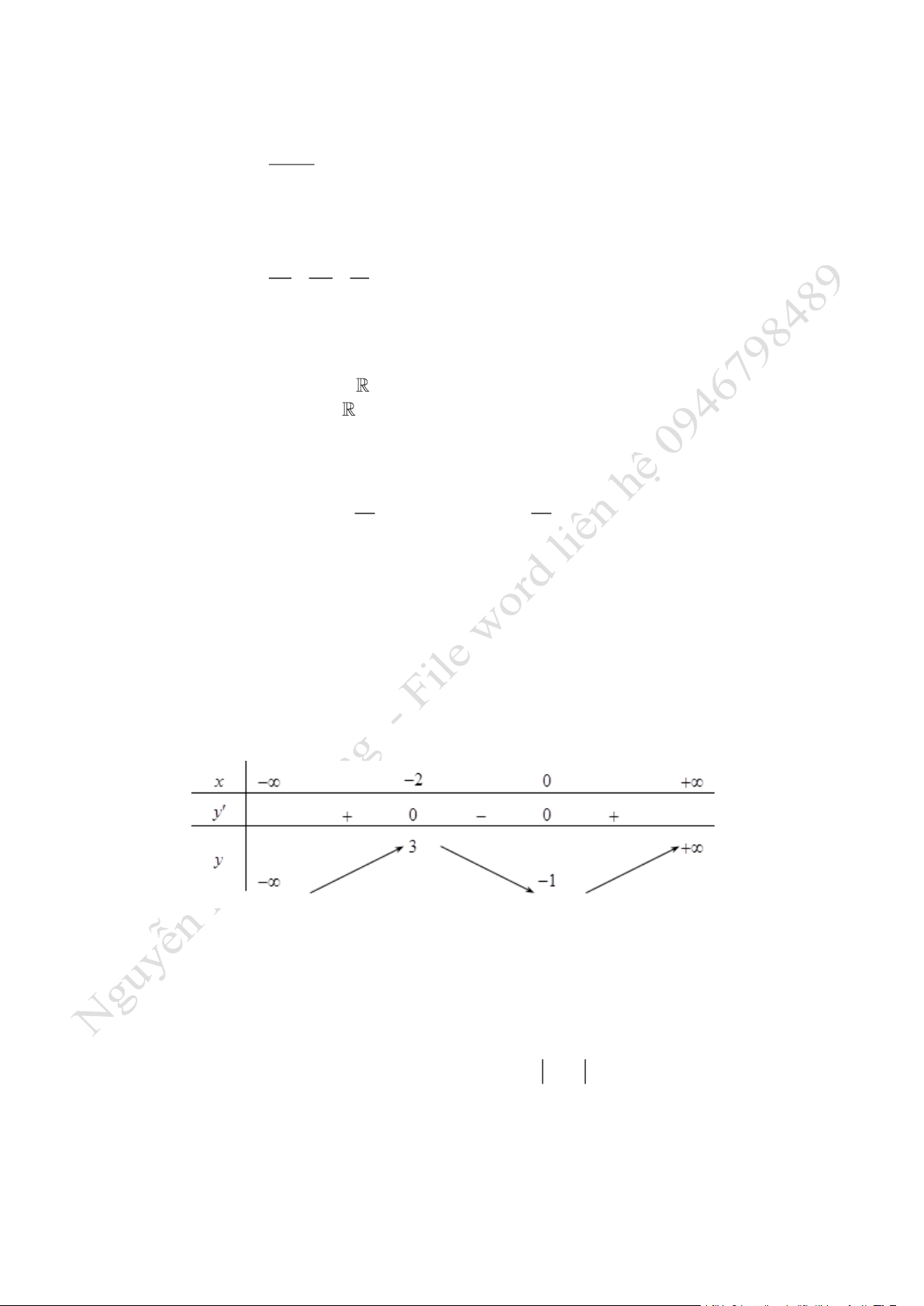
Câu 6: Cho hàm số có bảng biến thiên dưới đây. Phát biểu nào là đúng?
A. Giá trị cực tiểu cùa hàm số là
0
.
B. Giá trị cực đại cùa hàm số là
2−
.
C. Hàm số đạt cực tiểu tại
1x=−
và đạt cực đại tại
3x=
.
D. Hàm số đạt cực đại tại
2x=−
và đạt cực tiểu tại
0x=
.
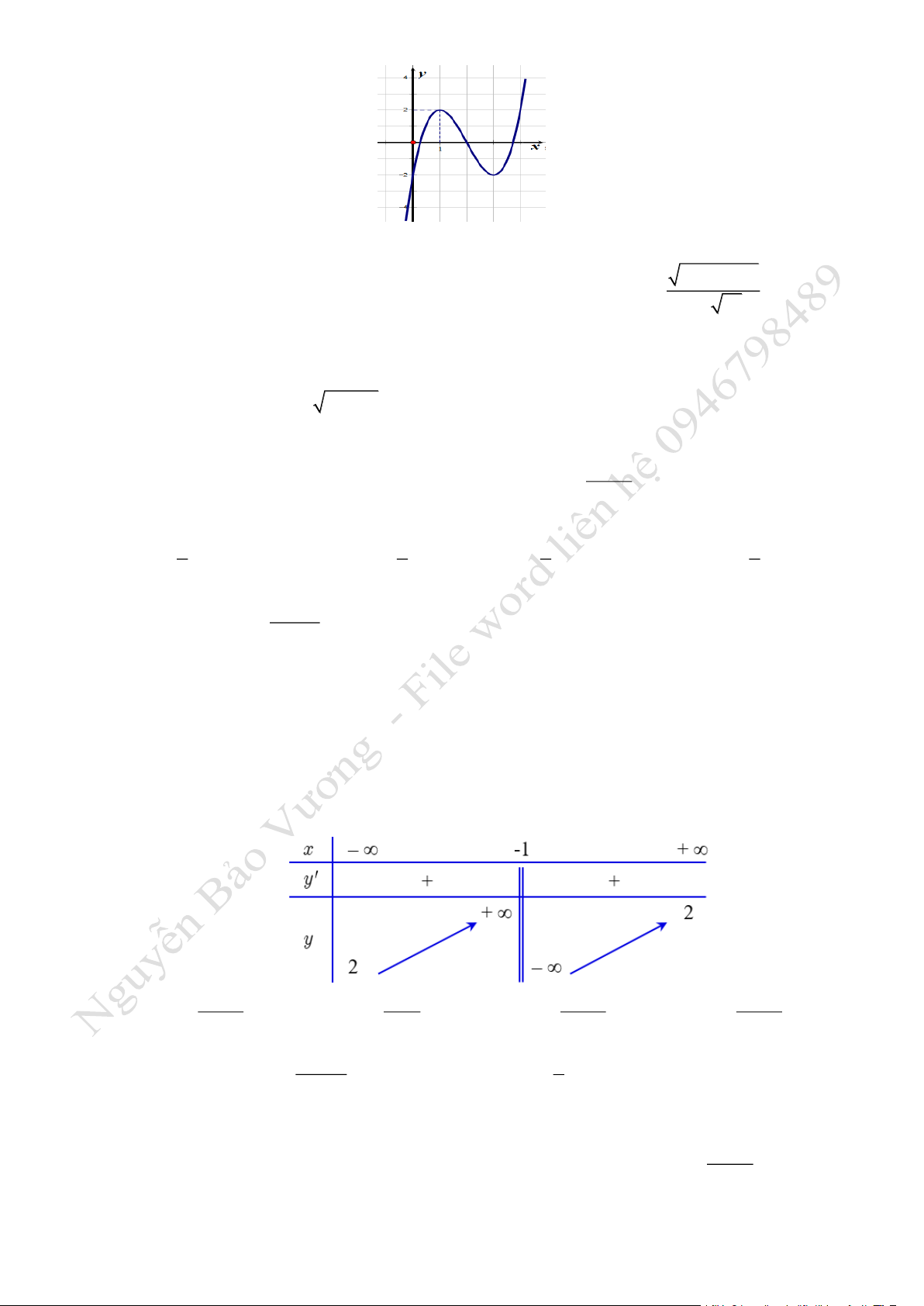
Câu 7: Cho hàm số
( )
32
6 9 2y f x x x x= = − + −
có đồ thị là đường cong trong hình vẽ bên. Tìm tất cả
các giá trị thực của tham số
m
sao cho phương trình
( )
f x m=
có
6
nghiệm thực phân biệt.