Phương Pháp Máy Phát Tương
Đương
Định Lý Thevenin-Norton
Giáo viên hướng dẫn: Trương Đình Tòa
Nhóm thực hiện: nhóm 5
Lê Anh Đức Phan Minh Tiến
VũThanh Huy Lâm Hoàng Minh Tuấn
Hoàng Văn Hưng Nguyễn Thành Trung
Nguyễn ThịNgọc Lan Phạm ThịHuyền Trang
Nguyễn ThịMỹLinh Nguyễn ThịThanh Thảo
Lê Hoàng Anh Linh Lê ThịCẩm Tú
Lê Thanh NhẩnLưu Đình Trác
Đàng ThịKim Sắc
Nội Dung Trình Bày:
I. Định lý Thevenin-Norton
II. Phương Pháp
III. Các ví dụ
IV. Kết luận
I. Định lý Thevenin-Norton
1. Định lý: Một mạch điện phức tạp có
chứa nhánh a, b có thểcoi là tương đương
một máy phát có suấtđiệnđộng E bằng
hiệuđiện thế đo được giữa a, b khi a, b hở
mạch và có điện trởnội r (trong) bằng điện
trở đo được giữa a, b khi thay tất cảcác
suấtđiệnđộng của mạch điện bằng điện
trởnội
I= a1ε1+a2ε2+………+anεn+bU(1)
2. Chứng minh định lý
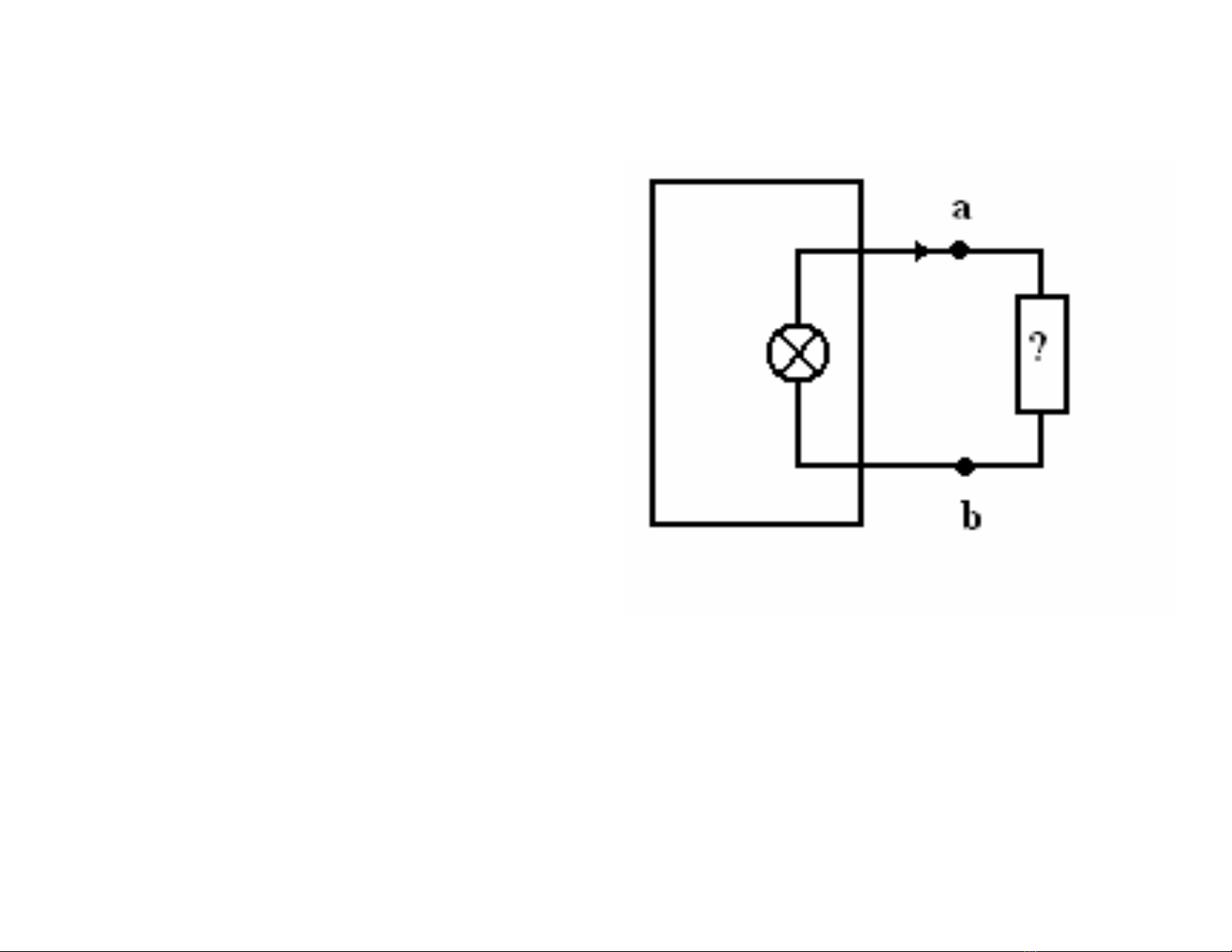
Giảsửtrên đoạn mạch a, b
có dòng điện có hướng chạy
ra khỏi a, có cuờng độ là I,
còn hiệuđiện thếgiữa a, b
là Uab=U
Ta có thểbiểu diễn I là một
hàm tuyến tính thuần nhất
của U và của các suấtđiện
động trong mạch điện