Đề thi đề xuất 1 – Kiểm tra Học kỳ 1 năm học 2010-2011 – Môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 1
Trường THPT Vinh Xuân KIỂM TRA HỌC KỲ I - NĂM HỌC 2010-2011
Tổ Toán Tin MÔN TOÁN LỚP 12 ( Thời gian 90 phút )
-----------
ĐỀ THI ĐỀ XUẤT 1
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM
A- PHẦN CHUNG ( 7 điểm )
Câu Nội dung Điểm
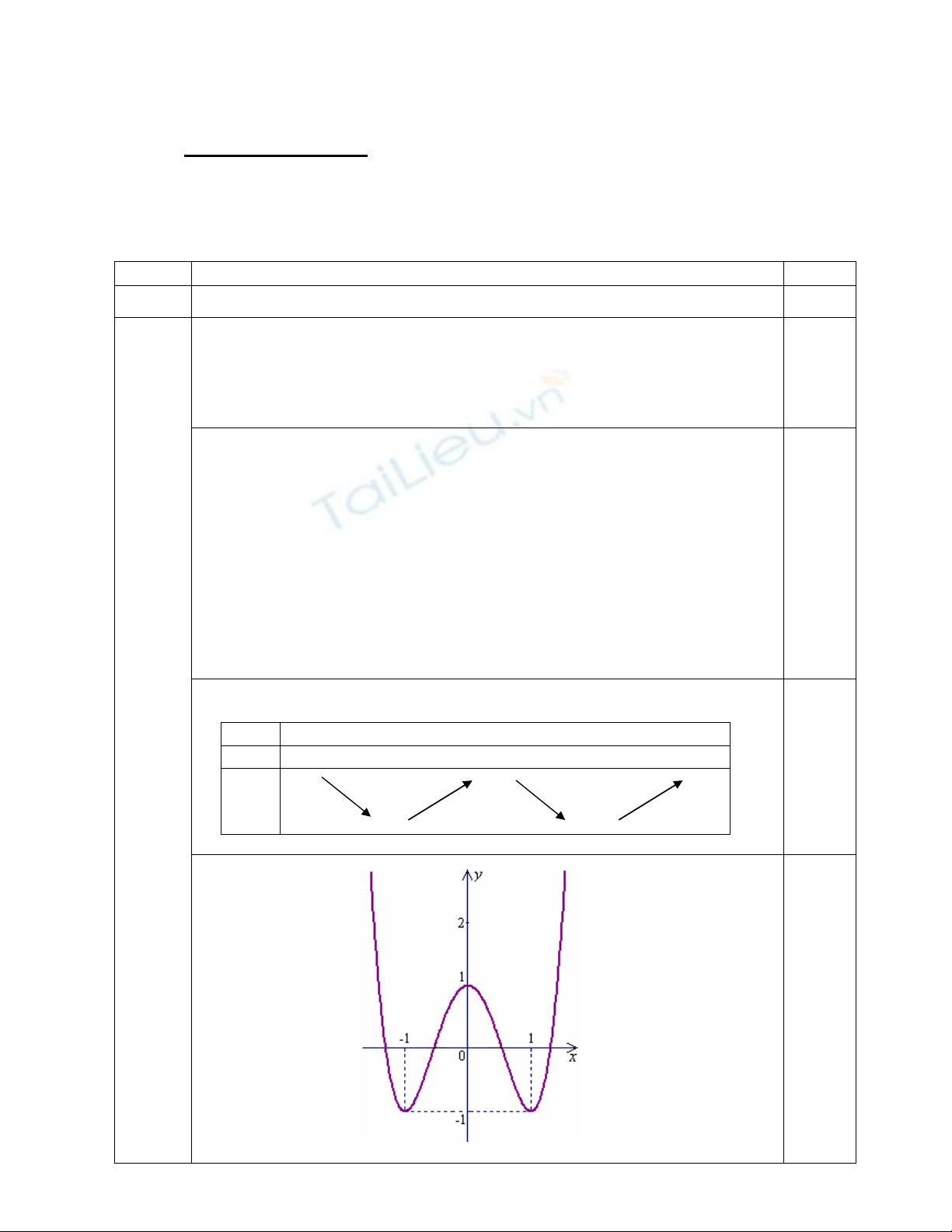
Câu 1 Cho hàm số 4 2
2 4 1
y x x
3,00
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 4 2
2 4 1
y x x
1.Tập xác định
D
¡
.
2. Sự biến thiên
a. Giới hạn: lim
xy


; lim
xy


0,50
b. Chiều biến thiên:
3 2
' 8 8 8 1
y x x x x
;
0
' 0
1
x
yx
' 0, 1;0 1;y x

nên hàm số đồng biến trên các khoảng
1;0
và
1;

.
' 0, ; 1 0;1
y x  nên hàm số nghịch biến trên các khoảng
; 1

và
0;1
.
Hàm số đạt cực đại tại
0
x
và CD
1
y
.
Hàm số đạt cực tiểu tại
1
x
và CT
1
y
0,50
c. Bảng biến thiên
x

1
0 1

y’
0 + 0
0 +
y

1

1
1
0,50
1.1
( 2,00 )
3. Đồ thị
0,50
Đề thi đề xuất 1 – Kiểm tra Học kỳ 1 năm học 2010-2011 – Môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 2
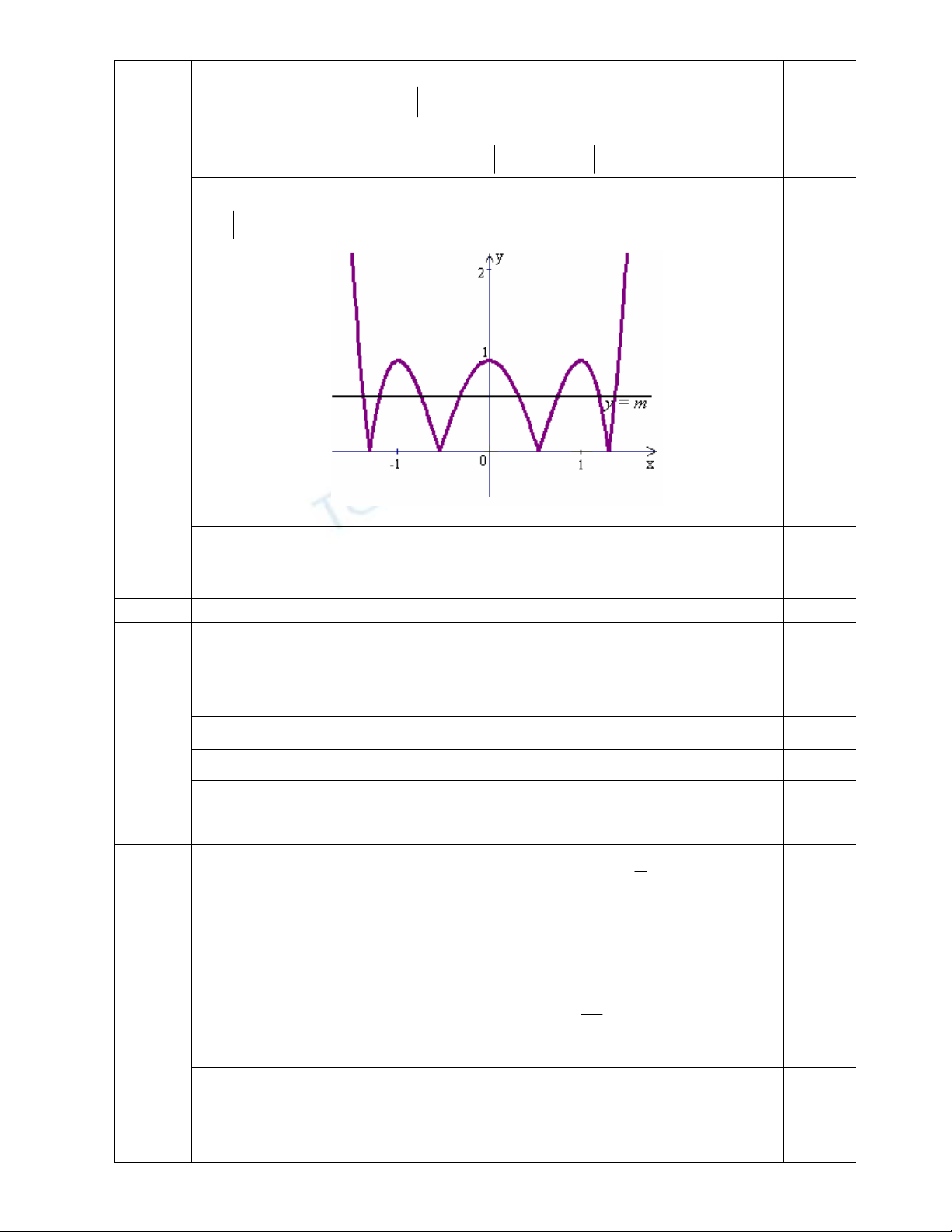
Tìm tham số m để phương trình sau có tám nghiệm phân biệt
4 2
2 4 1
x x m
(1)
Phương trình (1) có tám nghiệm phân biệt khi và chỉ khi đường thẳng
y m
cắt đồ thị
1
( )
C
của hàm số 4 2
2 4 1
y x x
tại 8 điểm phân biệt .
0,25
Từ đồ thị (C) của hàm số 4 2
2 4 1
y x x
suy ra đồ thị
1
( )
C
của hàm số
4 2
2 4 1
y x x
như sau:
0,50
1.2
( 1,00 )
Dựa vào đồ thị
1
( )
C
suy ra đường thẳng
y m
cắt đồ thị
1
( )
C
tại 8 điểm
phân biệt khi và chỉ khi
0 1
m
.
0,25
Câu 2 2,00
Giải phương trình 21 1
5 .3 1
x x
Lấy lôgarit cơ số 5 hai vế của phương trình ta được
2
5 5
1 1
log 5 .3 log 1
x x 2
5 5
1 1
log 5 log 3 0
x x
0,25
25
1 1 log 3 0
x x
0,25
5
1 1 1 log 3 0
x x x
5
1 1 log 3 0
x x
0,25
2.1
(1,00)
5
1
1 log 3
x
x
Vậy phương trình có 2 nghiệm
1
x
và
5
1 log 3
x
0,25
Tìm giá trị lớn nhất của hàm số
2
5
ln 12
6
y x x x
Tập xác định của hàm số
3;4
D .
0,25
Ta có 2
1 2 5
'
12 6
x
y
x x
2
2
5 7 66
6 12
x x
x x
' 0
y
2
5 7 66 0
x x
3
x
hoặc
22
5
x
Vì
3;4
x nên ta chọn
3
x
.
0,25
2.2
(1,00)
Bảng biến thiên
Đề thi đề xuất 1 – Kiểm tra Học kỳ 1 năm học 2010-2011 – Môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 3
x
22
5
3
3 4
y’
0 + + 0
y
5
ln6
2


0,25
Từ bảng biến thiên suy ra
3;4
5
ln6
2
max CD
yy
đạt được khi
3
x
.
0,25
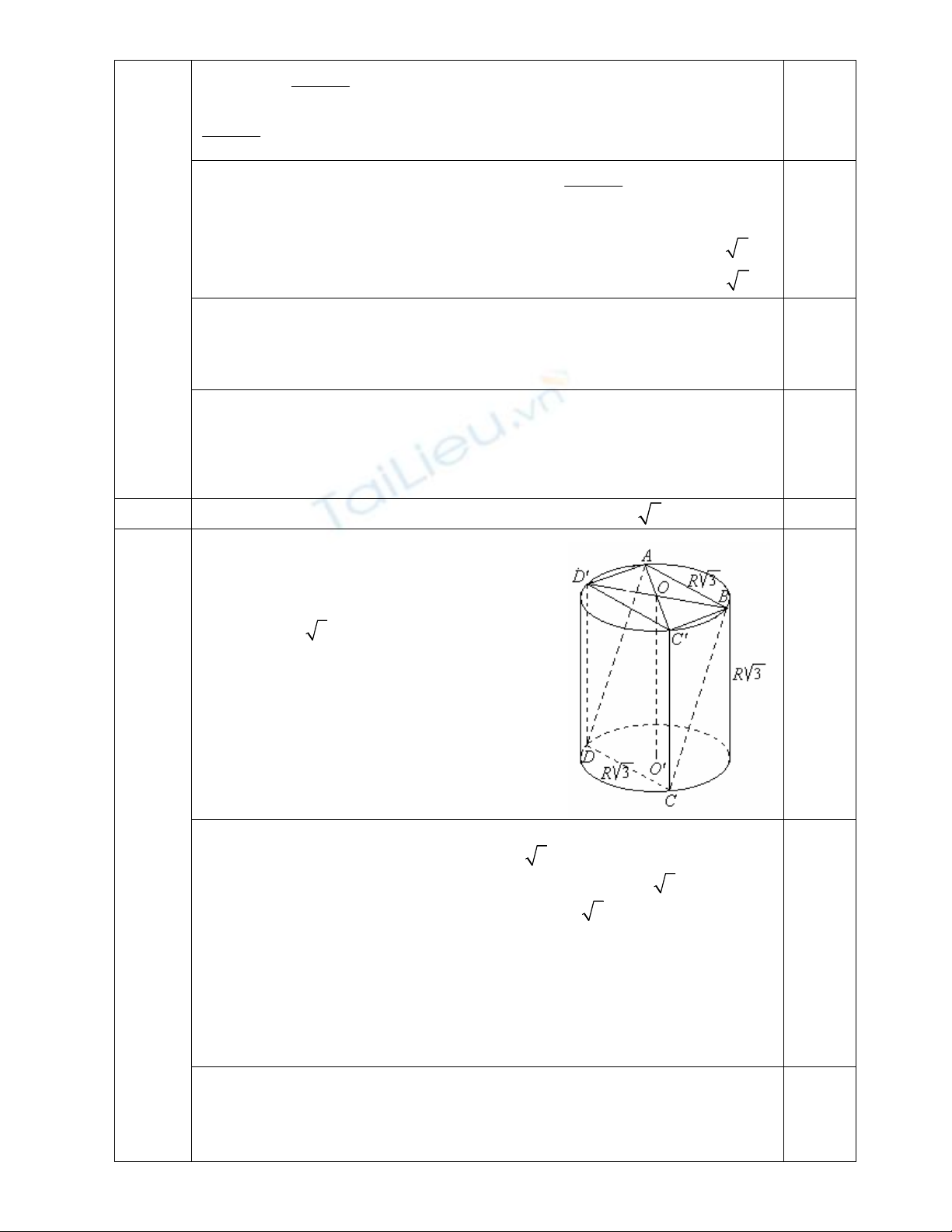
Câu 3 Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a,
·
0
60
ABC
2,00
Tính thể tích tứ diện SBMD theo a.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi cạnh a và
·
0
60
ABC nên tam giác ABC là tam giác
đều, suy ra
AC a
và
3
2
a
BO . Do đó
2 3
BD BO a
.
Từ tam giác vuông SAC ta có
2 2 2 2
3
SA SC AC a
3
SA a
.
0,25
Áp dụng công thức tỉ số thể tích hai khối chóp tam giác có chung đỉnh ta có
1
. .
2
SBMD
SBCD
V SB SM SD SM
V SB SC SD SC
1
2
SBMD SBCD
V V
0,25
Thể tích khối chóp SBCD là
3
1 1
. . .
3 6 4
SBCD BCD
a
V S SA BD OC SA
0,25
3.1
(1,00)
Vậy thể tích tứ diện SBMD là
3
1
2 8
SBMD SBCD
a
V V
.
0,25
3.2
(1,00) + Xác định tâm và tính bán kính mặt cầu ngoại tiếp tứ diện SBMD.
Đề thi đề xuất 1 – Kiểm tra Học kỳ 1 năm học 2010-2011 – Môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 4
Do OM là đường trung bình của tam giác SAC nên
3
2 2
SA a
OM .
Suy ra
3
2
a
OB OD OM nên O là tâm đường tròn ngoại tiếp tam
giác BMD (1)
Mặt khác, ta có
//
OM SA
và
( )
SA ABCD
nên
( )
OM ABCD
suy ra
OM AC
, kết hợp với
BD AC
ta có
( )
AC BMD
(2)
Từ (1) và (2) suy ra đường thẳng AC là trục của tam giác BMD.
Trong mặt phẳng (SAC) dựng đường trung trực của đoạn thẳng SM cắt
đường thẳng AC tại điểm I. Khi đó I là tâm mặt cầu ngoại tiếp tứ diện
SBMD, bán kính mặt cầu là
r IS
.
0,50
Gọi N là trung điểm của đoạn thẳng SM thì
IN SM
và
3 3 3
.2
4 4 2
a
NC SC a
Từ hai tam giác vuông đồng dạng SAC và INC ta có
SA AC
IN NC
.
SA NC
IN
AC
3
3.
3 3
2
2
a
a
a
a
Từ tam giác vuông ISN ta có
22
2 2 2 2
3 3
7
2 2
a a
IS IN SN a
7
IS a
.
Vậy bán kính mặt cầu ngoại tiếp tứ diện SBMD là
7
r IS a
.
0,50
B- PHẦN RIÊNG ( 3 điểm )
Phần 1: Theo chương trình chuẩn
Câu 4a
2,00
Giải bất phương trình
2
2 4 1
4
log 1 3log 1 log 1 2
x x x
Điều kiện
1
x
.
0,25
Bpt
2
2 2 2
3 1
log 1 log 1 log 1 2
2 2
xxx
2
2 2
log 1 log 1 2
x x
2
2 2
log 1 log 1 2 0
x x
0,25
Đặt
2
log 1
t x
bất phương trình trở thành 2
2 0
t t
2 1
t
0,25
4a.1
(1,00)
Suy ra
2
2 log 1 1
x
1
1 2
4
x
5
3
4
x
( thỏa mãn
1
x
)
Vậy bất phương trình có tập nghiệm là 5
;3
4
S
.
0,25
4a.2
(1,00) Tìm tham số m để đường thẳng
y x m
cắt đồ thị hàm số ...
Phương trình hoành độ giao điểm của đường thẳng
y x m
và đồ thị
Đề thi đề xuất 1 – Kiểm tra Học kỳ 1 năm học 2010-2011 – Môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 5
hàm số
2 8
1
x
y
x
là
2 8
1
x
x m
x
2
( ) 3 8 0
f x x m x m
(1) ( với
1
x
)
0,25
Đường thẳng
y x m
cắt đồ thị hàm số
2 8
1
x
y
x
tại hai điểm phân
biệt A và B khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 1
2
3 4 8 0
(1) 1 3 8 0
m m
f m m
2
2 23 0
6 0
m m
1 2 6
1 2 6
m
m
(*)
0,25
Khi đó gọi tọa độ giao điểm là
1 1
;
A x y
và
2 2
;
B x y
, trong đó
1 2
,
x x
là
nghiệm của phương trình (1) và 1 1
y x m
, 2 2
y x m
. Theo định lý
Vi-ét ta có 1 2 1 2
3, 8
x x m x x m
.
0,25
Từ tam giác OAB vuông góc tại O ta có
OA OB
. 0
OA OB
uuur uuur
1 2 1 2
0
x x y y
1 2 1 2
0
x x x m x m
2
1 2 1 2
2 0
x x m x x m
2
2 8 3 0
m m m m
16 0
m
16
m
( thỏa mãn điều kiện (*) )
0,25
Câu 5a Cho hình trụ có bán kính đáy bằng R và trục
' 3
OO R
... 1,00
Vì mặt phẳng (ABCD) cắt hai mặt phẳng đáy
song song (O) và (O’) theo hai giao tuyến AB
và CD nên
//
AB CD
. Kết hợp với giả thiết
3
AB CD R suy ra tứ giác ABCD là hình
bình hành. (*)
0,25
Dựng hai đường sinh CC’ và DD’ của hình trụ, khi đó CDD’C’ là hình chữ
nhật, suy ra
' '//
C D CD
và
' ' 3
C D CD R (1)
Vì ABCD là hình bình hành nên
//
AB CD
và
3
AB CD R ( 2)
Từ (1) và (2) suy ra
// ' '
AB C D
và
' ' 3
AB C D R
Do đó tứ giác ABC’D’ là hình bình hành, nhưng ABC’D’ nội tiếp đường
tròn (O) nên ABC’D’ là hình chữ nhật.
Suy ra
'
AB AD
, mà
'
AB DD
( vì
( ) '
mp O DD
) nên
'
AB mp ADD
, do đó
AB AD
(**)
Từ (*) và (**) suy ra ABCD là hình chữ nhật .
0,25
Mặt khác, từ ABC’D’ là hình chữ nhật suy ra BD’ là đường kính của đường
tròn đáy, do đó
' 2
BD R
.
Từ tam giác vuông BC’D’ ta có
2 2 2 2 2 2
' ' ' ' 4 3
BC BD C D R R R
'
BC R