wWw.VipLam.Net
Voõ Duy Minh ÑEÀ OÂN TAÄP HOÏC KYØ I
KI M TRA H C KỲ I – NĂM H C 2012 – 2013Ể Ọ Ọ
Môn TOÁN – L p 12 THPTớ
Th i gian làm bàiờ: 90 phút
Đ 1 :Ề Không k th i gian giao đ .ể ờ ề
I. PH N CHUNG CHO T T C THÍ SINH: ( 7 đi m )Ầ Ấ Ả ể
Câu 1: ( 3.0 đi m )ể
Cho hàm s ố
33 3 ( )y x x C=−−
1/ Kh o sát s bi n thiên và v đ th ả ự ế ẽ ồ ị
( )C
c a hàm s .ủ ố
2/ Bi n lu n theo m s nghi m c a ph ng trình ệ ậ ố ệ ủ ươ
33 0x x m− − =
Câu 2: ( 2.0 đi m ).ể
Gi i các ph ng trìnhả ươ
1/
2
8 1 3
2 4
x x x
− + −
=
2/
( ) ( )
2
2
2 2
log 2 3 2log 2 3 2x x+ − + =
Câu 3: ( 1.0 đi m )ể
Tìm giá tr l n nh t, giá tr nh nh t c a hàm s : ị ớ ấ ị ỏ ấ ủ ố
()
2
1
( ) 12 3
2
y f x x x= = + −
trên
[ ]
2; 2−
Câu 4: ( 1.0 đi m )ể
Cho
ABC
∆
vuông cân t i ạA, đ ng th ng ườ ẳ
đi qua A vuông góc v i ớBC t i ạH, có
2AH a=
.
Cho hình
ABC
∆
quay quanh đ ng th ng ườ ẳ
đ c m t hình tròn xoay. Tính di n tích m t xungượ ộ ệ ặ
quanh c a hình tròn xoay và th tích c a kh i tròn xoay t o thành.ủ ể ủ ố ạ
II. PH N RIÊNG – PH N T CH N: ( 3.0 đi m ).Ầ Ầ Ự Ọ ể ( Thí sinh làm m t trong hai ph n )ộ ầ
1. Theo ch ng trình chu n.ươ ẩ
Câu 5a: ( 2.0 đi m )ể
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông t i ạA và B;
2 2 2AD AB BC a
= = =
;
( )
; 4SA ABCD SC a⊥ =
, M là trung đi m c a c nh ể ủ ạ AD.
1/ Tính th tích c a kh i chóp ể ủ ố
.S CMD
.
2/ Xác đ nh tâm ịI, bán kính và tính di n tích xung quanh c a hình c u ngo i ti p hình chópệ ủ ầ ạ ế
.S ABCM
.
Câu 6a: ( 1.0 đi m )ể
Cho hàm s ố
( )
2
1
x
y C
x
=−
. Tìm các đi m trên đ th ể ồ ị
sao cho kho ng cách t đi m đó đ nả ừ ể ế
đ ng ti m c n đ ng b ng hai l n kho ng cách t đi m đó đ n đ ng ti m c n đ ng ngang c a đườ ệ ậ ứ ằ ầ ả ừ ể ế ườ ệ ậ ứ ủ ồ
th .ị
2. Theo ch ng trình nâng cao.ươ
Câu 5b: ( 2.0 đi m )ể
Cho hình chóp tam giác đ u ề
.S ABC
có đáy
ABC
là tam giác đ u c nh ề ạ a, m t bên h p v i m tặ ợ ớ ặ
đáy m t góc ộ
0
60
.
1/ Tính th tích c a kh i chóp ể ủ ố
.S ABC
.
2/ Xác đ nh tâm ịI, bán kính và tính di n tích xung quanh c a hình c u ngo i ti p hình chópệ ủ ầ ạ ế
.S ABC
.
Câu 6b: ( 1.0 đi m )ể
wWw.VipLam.Net
Voõ Duy Minh ÑEÀ OÂN TAÄP HOÏC KYØ I
Đ nh ịm đ hàm s ể ố
( )
22
2
x x m
y C
x
− +
=+
đ t c c ti u t i ạ ự ể ạ
2.x=
______________H t______________ế
KI M TRA H C KỲ I – NĂM H C 2012 – 2013Ể Ọ Ọ
Môn TOÁN – L p 12 THPTớ
Th i gian làm bàiờ: 90 phút
Đ 2 :Ề Không k th i gian giao đ .ể ờ ề
I PH N CHUNG CHO T T C THÍ SINH Ầ Ấ Ả (7,0 đi mể)
Câu I (2,5 đi mể)
Cho hàm s ố
3 2
( ) 3y f x x x= = +
.
1) Kh o sát s bi n thiên và v đ th (ả ự ế ẽ ồ ị C) c a hàm s .ủ ố
2) Vi t ph ng trình ti p tuy n c a đ th (C) t i đi m có tung đ b ng 0.ế ươ ế ế ủ ồ ị ạ ể ộ ằ
Câu II (1,5 đi mể)
1) Tìm giá tr nh nh t và giá tr l n nh t c a hàm s ị ỏ ấ ị ớ ấ ủ ố
( ) 2
y f x x 9 x= = −
.
2) Gi i ph ng trình ả ươ
1 1
12.4 2.6 9
x x x+ +
− =
Câu III (3,0 đi mể)
Cho kh i chóp ố
.S ABCD
có đáy ABCD là hình ch nh t v i ữ ậ ớ
, 2AB a BC a= =
, c nh bên SC t oạ ạ
v i đáy m t góc ớ ộ
0
45
và SA vuông góc v i đáy.ớ
1) Tính th tích kh i ể ố chóp
.S ABCD
2) Xác đ nh tâm và tính bán kính m t c u ngo i ti p hình chóp ị ặ ầ ạ ế
.S ABCD
.
3) G i ọO là trung đi mể SB , so sánh th tích hai kh i t di n ể ố ứ ệ
SAOC
và OACD.
II PH N RIÊNG Ầ(3,0 đi mể)
Thí sinh ch đ c làm m t trong hai ph n ỉ ượ ộ ầ ( ph n 1 ho c ph n 2ầ ặ ầ ).
1. Theo ch ng trình chu nươ ẩ
Câu IVa (3,0 đi mể)
1. Tìm các đ ng ti m c n c a đ th hàm s : ườ ệ ậ ủ ồ ị ố
2 1
1
x
yx
+
=−
2. Gi i ph ng trình: ả ươ
2 2
2 1 2
3 3 4.
x x x x− + −
+ =
3. Gi i b t ph ng trình: ả ấ ươ
2
3 3
log ( 1) log ( 1) 12.x x− − −
2. Theo ch ng trình nâng caoươ
Câu IVb (3,0 đi mể)
1. Tìm các đ ng ti m c n c a đ th hàm s : ườ ệ ậ ủ ồ ị ố
22 5
1
x x
yx
− +
=−
2. Gi i h ph ng trình: ả ệ ươ
3
1
9
log 6
log 12
xy
x
y
=
=
3. Cho hàm s ố
.
( )
1
x
x
e
f x
e
=+
Tính
(ln 3).f
--- H t ---ế
wWw.VipLam.Net
Voõ Duy Minh ÑEÀ OÂN TAÄP HOÏC KYØ I
H NG D N CH MƯỚ Ẫ Ấ
(Đáp án đ thi g m 4 trang)ề ồ
wWw.VipLam.Net
Voõ Duy Minh ÑEÀ OÂN TAÄP HOÏC KYØ I
CÂU N i dungộĐi mể
1(3.0 đi m)ể
1.1 2.0
+ T p xác đ nh D ậ ị
.
=
ﾡ
+
lim ; lim
x x
y y
+ −
= + = −
0.5
( )
( )
2 2
2
' 3 3 3( 1)
1 1 5
' 0 1 0 1 1 1
y x x
x y
y x x y
= − = −
= = −�
= − =� � = − = −�
0.25
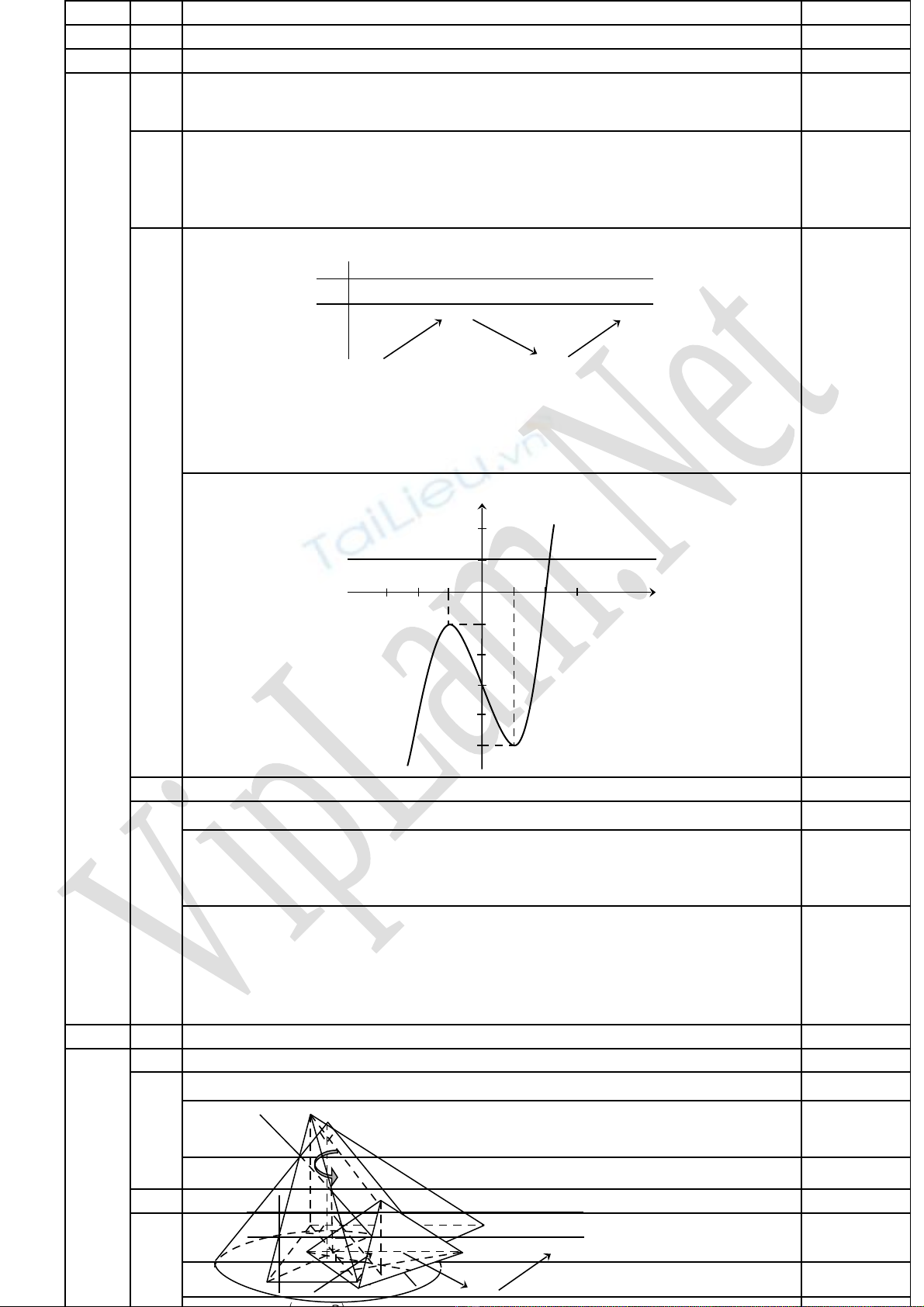
BBT:
Hàm s đ ng bi n trên các kho ng ố ồ ế ả
( ; 1);(1; )− − +
và ngh ch bi n trênị ế
kho ng ả
( 1;1)−
.
Hàm s đ t c c ti u t i ố ạ ự ể ạ
1x
=
và giá tr c c ti u ị ự ể
(1) 5
CT
y y= = −
Hàm s đ t c c đ i t i ố ạ ự ạ ạ
1x
= −
và giá tr c c ti u ị ự ể
( 1) 1
CD
y y= − = −
0.5
0.25
Đ th đi qua các đi m ồ ị ể
(0; 3);(2; 1);( 2; 5)− − − −
.
0.5
1.2 1.0
Ph ng trình: ươ
3 3 3
3 0 3 3 3 3 (1)x x m x x m x x m− − = − = − − = −� �
0.25
Đ t ặ
33 3 ( ); 3y x x C y m= − − = −
là đ ng th ng (d) cùng ph ng v i Ox.ườ ẳ ươ ớ
Ph ng trình (1) là ph ng trình hoành đ giao đi m c a (d) và (C).ươ ươ ộ ể ủ
S giao đi m c a (d) và (C) là s nghi m c a ph ng trình (1).ố ể ủ ố ệ ủ ươ 0.25
+
1m> −
ho c ặ
5m< −
: (d) và (C) có 01 đi m chungể
Pt (1) có 01 nghi mệ
+
1m= −
ho c ặ
5m= −
: (d) và (C) có 02 đi m chungể
Pt (1) có 02 nghi mệ
+
5 1m− < < −
: (d) và (C) có 03 đi m chungể
Pt (1) có 03 nghi mệ0.5
2(2.0 đi m)ể
2.1 1.0
2 2
8 1 3 8 2 6
2 4 2 2
x x x x x x− + − − + −
= =�
0.25
2 2 3
8 2 6 5 6 0 2
x
x x x x x x
= −
− + = − + + =� � � = −
0.5
V y, t p nghi m c a ph ng trình: ậ ậ ệ ủ ươ
{ }
3; 2S= − −
0.25
2.2 1.0
Đi u ki n: ề ệ
3
2
x> −
0.25
( ) ( ) ( ) ( )
2
2 2
2 2 2 2
log 2 3 2log 2 3 2 4log 2 3 2 log 2 3 2 0x x x x+ − + = + − + − =�
0.25
Đ t ặ
( )
2
log 2 3t x= +
–1 1
x
y'
y
0
0
−
+
++–
–1
–5
–2
–5
–1
–1
–3
3y m
= −
O
x
y
2
A
BC
H
B
A
S
C
D
M
O
I
N
A
S
B
C
M
N
EI
O
–6 2
x
y'
y
0
0
−
+
++–
CĐ
CT