Trang 1/6
Câu áp án im
I
(2.0 im)
1. (1.0 im) Kho sát…
• Tp xác nh:
=
.
• S bin thiên:
→−∞
= +∞
,
→+∞
= +∞
0.25
= + = ⇔ = = −

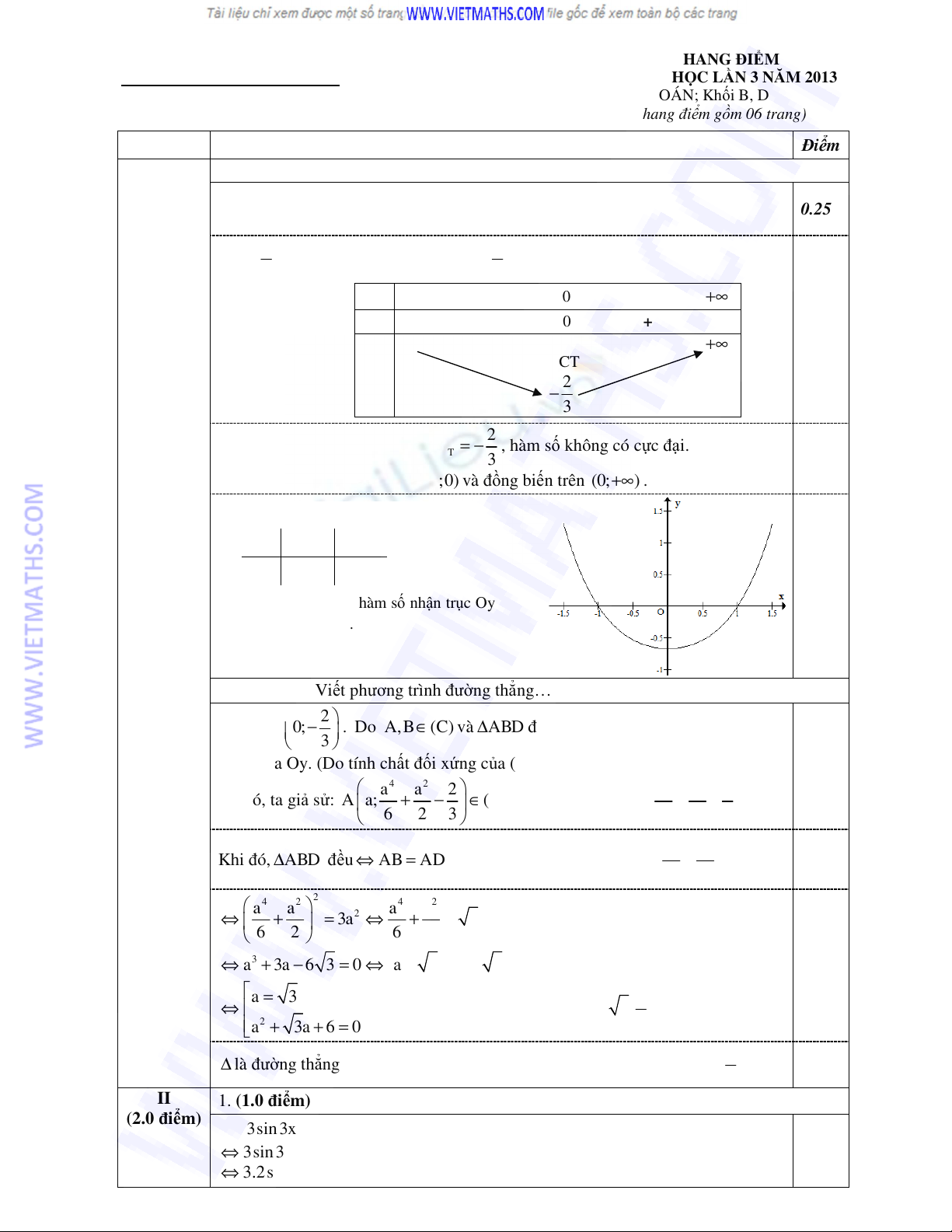
Bng bin thiên:
x
−∞
0
+∞
– 0 +
y
+∞
+∞
CT
−
0.25
Hàm s t CT ti
=
;
= −
, hàm s không có cc i.
Hàm s nghch bin trên
−∞
và ng bin trên
+∞
. 0.25
0.25
2. (1.0 im) Vit phng trình ng thng…
Ta có:
−
. Do
∈
và
∆
u
AB//Ox và A, B i xng
nhau qua Oy. (Do tính cht i xng ca (C))
Do ó, ta gi s:
+ − ∈

vi
>
− + −
0.25
Khi ó,
∆
u
⇔ = ⇔ = ⇔ = + +
0.25
⇔ + = ⇔ + =
(do
>
)
⇔ + − = ⇔ − + + =
=
⇔
+ + = ∆ = − <

0.25
∆
là ng thng i qua A và song song Oy
phng trình t
∆
là
= ⋅
0.25
II
(2.0 im)
1. (1.0 im) Gii phng trình:
+ + − =
⇔ + + − =
⇔ − + − =
 
0.25
S GD & T BC NINH
TRNG THPT LÝ THÁI T ÁP ÁN – THANG IM
 THI TH I HC LN 3 NM 2013
Môn: TOÁN; Khi B, D
(áp án – thang im gm 06 trang)
•  th:
x
−
y 0 0
- Nhn xét:  th hàm s nhn trc Oy
làm trc i xng.
Trang 2/6
II
(2.0 im)
⇔ − + − =
   
⇔ − − =
   
0.25
π
= =
− =
⇔ ⇔
− =
=
  



0.25
π π
= + π = + π
π π
⇔ = + π ⇔ = + π
= ± + π = ± + π




! !
Vy nghim ca phng trình ã cho là:
π π
= + π = + π = ± + π
!
0.25
2. (1.0 im) Gii h phng trình…
HPT
+ + = − =
⇔ ⇔
− − = − + + =
  
  
= + = + = +
⇔ ⇔ ⇔
+ + + = + = = −

"
   
0.25
a. Vi
=
=
"
vô nghim. 0.25
b. Vi
≠

, t (I)
= + − ⇔ = − + +

⇔ + − − =
⇔ − + + =
=
⇔
+ + = ∆ = − <
0.25
Vi
=

. Thay vào (I) ta c:
= =
⇔
=
=
Vy nghim ca phng trình ã cho là
(
)
.
0.25
III
(1.0 im)
Tính tích phân …
Ta có:
π π
+
= = + = +
" # $ # " "

Tính
π π
= = + − + +
" $ # $ $ $ #
ππ
π
π π
= − + = − + = − +
$
$ #$ $
0.5
Tính
π π π
= = ⋅ = + = ⋅
#
" # $ #$
  
0.25
Vy
π π
= + = − + + = + ⋅
" " "
0.25
Trang 3/6
IV
(1.0 im)
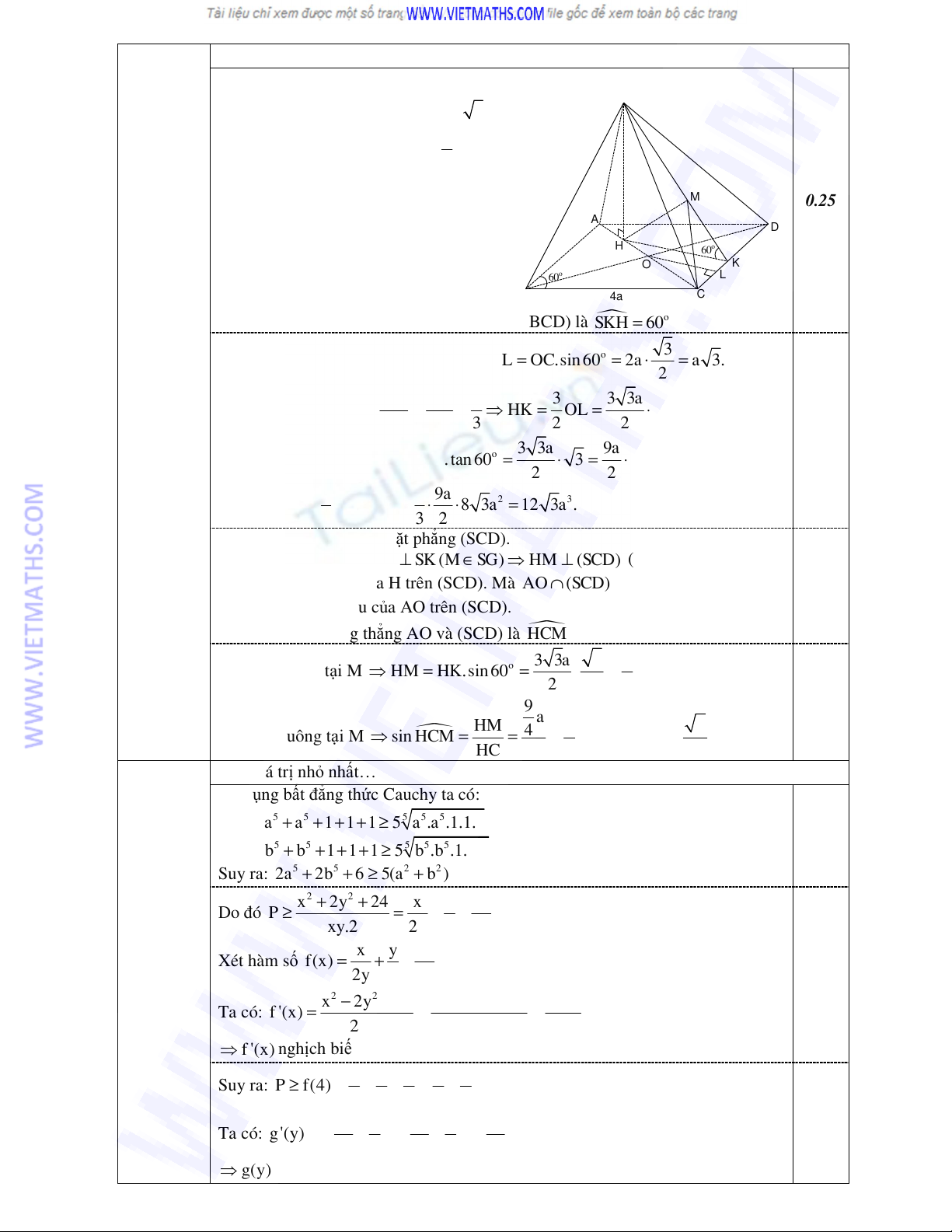
Tính th tích khi lng tr …
S
A
BC
D
H
K
L
M
O
60
o
60
o
4a
Do ó góc gia hai mt phng (SCD) và (ABCD) là
=
%&'
0.25
∆
(
vuông ti O có
== = =
⋅
( () (
∆
'&
có OL//HK
= = = = ⋅
() (
'& ()
'& '
∆
%'&
vuông ti H
= = ⋅ = ⋅
*
%' '& $
Vy
= = ⋅ ⋅ =
% 
*
+ %'%
0.25
Tính góc gi
a A
O
và
m
t ph
ng
(SCD)
.
Trong mp (SHK) k
⊥ ∈
⊥
', %&, %- ', %
(do
⊥
%'&
)
M là hình chiu ca H trên (SCD). Mà
∩ =
( %
MC là hình chiu ca AO trên (SCD).
Góc gia ng thng AO và (SCD) là
',
0.25
∆
', &
vuông ti M
= = ⋅ =
*
', '&
∆
',
vuông ti M
= = = = ⋅
*
',
',  ',
'
0.25
V
(1.0 im)
Tìm giá tr nh nht…
Áp dng bt ng thc Cauchy ta có:
+ + + + ≥ =
+ + + + ≥ =
. . . .  .
Suy ra:
+ + ≥ + ⇔ + ≤
. . .
0.25
Do ó
+ +
≥ = + +

/

Xét hàm s
= + +

0

vi
∈
1
và y là tham s.
Ta có:
− − − − −
= ≤ = < ∀ ∈
 
0  1
 
0
nghch bin trên
1
≥
0 0
0.25
Suy ra:
≥ = + + = + =
/ 0 2
 
vi
∈
1
Ta có:
= − + ≤ − + = − < ∀ ∈
2 1
 
2
nghch bin trên
≥ = + =
2 2 3 * 3
.
0.25
Ta có:
∆
= = =

% % 
T gi thit ta có: = =
' '( (
Trong mt phng (ABCD), g i L là
chân ng cao h t O ca
∆
(
K HK//OL
∈
& 
⊥
'&
(1)
Mà H là hình chiu ca S trên mt
phng (ABCD)
⊥
%'
(2)
T (1), (2)
⊥
%'&