TR NG THPT TR NG XUÂNƯỜ ƯỜ Đ THI H C KÌ I Ề Ọ
NĂM H C 2017-2018Ọ
MÔN TOÁN 12
Th i gian: 90 phútờ
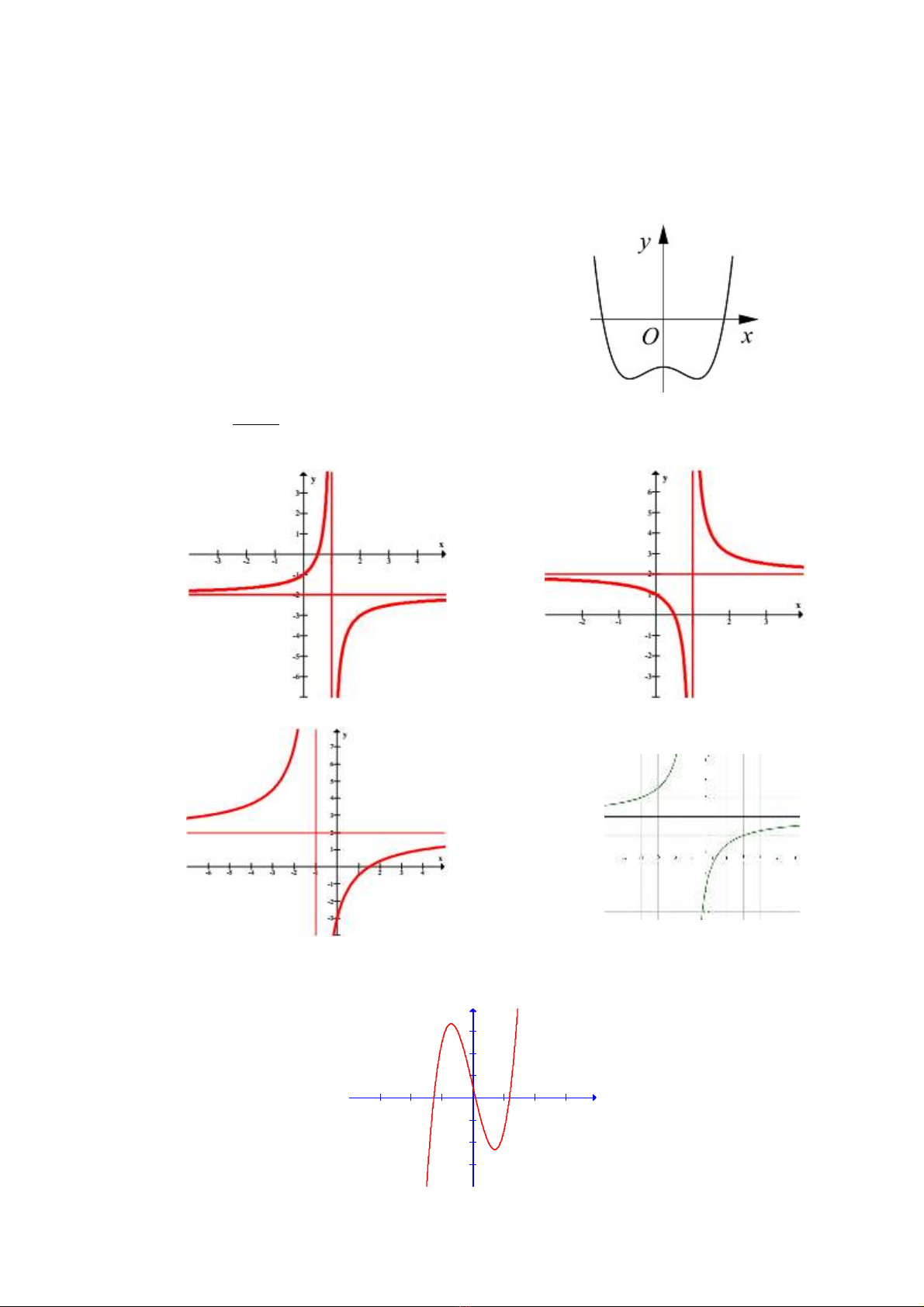
Câu 1. Đ th hình bên là đ th c a hàm s nào sau đây:ồ ị ở ồ ị ủ ố
A.
4 2 1y x x= − +
B.
4 2 1y x x= + −
C.
4 2 1y x x= − + −
D.
4 2 1y x x= − −
Câu 2:Hàm s ố
2 3
1
x
yx
−
=+
có đ th làồ ị
A. B.
C. D.
Câu 3:Đng cong trong hình làđ th c a m t hàm s trong b n hàm s d i đây. ườ ồ ị ủ ộ ố ố ố ướ Hàm s đó là ố
hàm s nào? ố
-6 -4 -2 2 4 6
-6
-4
-2
2
4
6
x
y
A.
3
3 1y x x
= − − +
. B.
3
4 6 1y x x
= − +
. C.
3
6 1y x x
= − +
. D.
4 2
3 1y x x
= − +
Câu 4: Ph ng trình ươ
có ba nghi m phân bi t khi và ch khi:ệ ệ ỉ
A.
3 1m
− < <
B.
1 3m
− < <
C.
1m
=
D.
0m
=
Câu 5:Hàm s nào sau đây đng bi n trên Rố ồ ế
A.
3 2
2 3 1y x x= − +
B.
3 2
3 3y x x x= − +
C.
4 2
4 1y x x= + −
D.
1
3 2
x
yx
−
=−
Câu 6:Ti p tuy n c a đ th hàm s ế ế ủ ồ ị ố
3 2
3 2y x x= − +
t i M(-1,-2) làạ
A.
9 2y x= −
B
9 7y x= +
. C.
24 2y x= −
D.
24 22y x= +
Câu 7: Hàm s ố
4
2
9 1
4
x
y x= − −
đng bi n trên:ồ ế
A.
( )
3, 2− −
và
( )
1,− +
B.
( )
3,0−
và
( )
3, +
C.
( )
3, 4−
và
( )
5, +
D.
( )
, 3− −
và
(0,3)
Câu 8:Xác đnh các ti m c n c a HS ị ệ ậ ủ
8 5
3
x
yx
+
=−
A.Ti m c n đng x=3;Ti m c n ngang ệ ậ ứ ệ ậ
8
3
y=
B. Ti m c n đng x=3;Ti m c n ngang ệ ậ ứ ệ ậ
5
3
y=
C.Ti m c n đng x=3;Ti m c n ngang ệ ậ ứ ệ ậ
5y= −
D.Ti m c n đng x=3;Ti m c n ngang ệ ậ ứ ệ ậ
8y= −
Câu 9: Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
2
4y x x= - -
.
A. -
2
B. -
3
C.-2
2
D.
2 3−
Câu 10: Ph ng trình đng ti m c n ngang c a đ th hàm s ươ ườ ệ ậ ủ ồ ị ố
2
2 1
4 2 1
x
y
x x
+
=+ +
là:
A.y=1 B.
0y
=
C.
1y
= −
D.
1; 1y y
= = −
Câu 11. S giao đi m c a đng cong ố ể ủ ườ
12
23
xxxy
và đng th ng y = 1 – 2x là:ườ ẳ
A. 1 B. 2 C. 3 D. 0
Câu 12. Tìm giá tr c a tham s ị ủ ố m đ hàm s ể ố
2
1
2 1
x m
yx
− −
=−
đt giá tr nh nh t trên đo nạ ị ỏ ấ ạ
[1;2]
b ng 0.ằ
A.
2m
=
B.
1m
=
C.
0m
=
D.
1m
= −
Câu 13: T ng các tung đ giao đi m c a đng cong (C): ổ ộ ể ủ ườ
3 2
2 4y x x x= + +
và đng th ngườ ẳ
= + +
2
(d):y x 13x 9
A.54 B.-1 C.2 D.3
Câu 14:Tìm s đng ti m c n c a đ th có b ng biên thiên làố ườ ệ ậ ủ ồ ị ả
+
∞
-
∞
-
∞
+
∞
0
_
x
y
/
y
+
∞
-
∞
_
-1
0
-2
+
-2
+
1
1
A. 4 B.3 C.2 D.1
Câu 15: Cho hàm s ố
4mx m
yx m
+
=+
v i m là tham s .G i S là t p t t c các giá tr nguyên c a m đớ ố ọ ậ ấ ả ị ủ ể
hs ngh ch bi n trên các kho ng xác đnh.Tìm s ph n t c a Sị ế ả ị ố ầ ử ủ
Câu 16. Giá tr c a m đ hàm s y = ị ủ ể ố
3
1
x3 – 2mx2 + (m + 3)x – 5 + m đng bi n trên R là:ồ ế
A.
1
m
B.
1
4
3 m
C.
4
3
m
D.
1
4
3 m
Câu 17. Đ th hàm s y = xồ ị ố 3 – ( 3m + 1)x2 + ( m2 + 3m + 2)x + 3 có đi m c c ti u và đi m ể ự ể ể
c c đi n m v hai phía c a tr c tung khi :ự ạ ằ ề ủ ụ
A. 1 < m < 2 B. 2 < m < 3 C. – 2 < m < - 1 D. – 3 < m < - 2
Câu 18. Hàm s y = mxố4 + 2(m – 2)x2 – 1 có 3 c c tr khi:ự ị
A. m < 2 B. m > 0 C. 0 < m < 2 D.
20
m
Câu 19. Giá tr c a m đ hàm s y = đt c c đi t i x = 0?ị ủ ể ố ạ ự ạ ạ
A. m = 2 B. m = 1 C. m = 1 ho c m = 2ặD. m = 6
Câu 20. Đ th hàm s y = - xồ ị ố 4 + 2mx2 có 3 đi m c c tr t o thành m t tam giác đu khi:ể ự ị ạ ộ ề
A. m =
33
B. m = 0, m =
33
C. m = 0 D. m = 0, m = 27
Câu 21. Cho a là s th c d ng. Vi t l i bi u th c ố ự ươ ế ạ ể ứ
6
2
2
1
.. aaa
d i d ng lũy th a v i s mũ ướ ạ ừ ớ ố
h u tữ ỉ :
A.
6
1
a
B.
3
8
a
C.
6
a
D.
6
17
a
Câu 22. Đo hàm c a hàm s ạ ủ ố
x
y
b ngằ
A.
ln' x
y
B.
1
.'
x
xy
C.
x
y
'
D.
ln
'
x
y
Câu 23. T p xác đnh c a hàm s ậ ị ủ ố
xy 3log2
là
A.
;3
B.
;3
C.
3;
D.
3;
Câu 24. T p xác đnh c a hàm s ậ ị ủ ố
5
2
1
xy
là
A.
1;1
B.
;11;
C.
1;1\ R
D.
1;1\ R
Câu 25. Tìm các nghi m c a ph ng trình ệ ủ ươ
813 1
x
A. x=4 B. x=5 C. x= 9 D. x=3
Câu 26. S nghi m c a ph ng trình ố ệ ủ ươ
xx 10log25log 2
là
A. 0 B. 1 C. 2 D. 3
Câu 27. Ph ng trình ươ
0453.49 xx
có t p nghi m b ng ậ ệ ằ
A.
9
B.
5;9
C.
2
D.
5log;2 3
Câu 28. Ph ng trình ươ
64ln23
2
2e
xx
có t ng bình ph ng các nghi m b ng ổ ươ ệ ằ
A. 3 B. 5 C. 9 D. 17
Câu 29. B t ph ng trình ấ ươ
7
9
9
732 2
xx
có t p nghi m làậ ệ
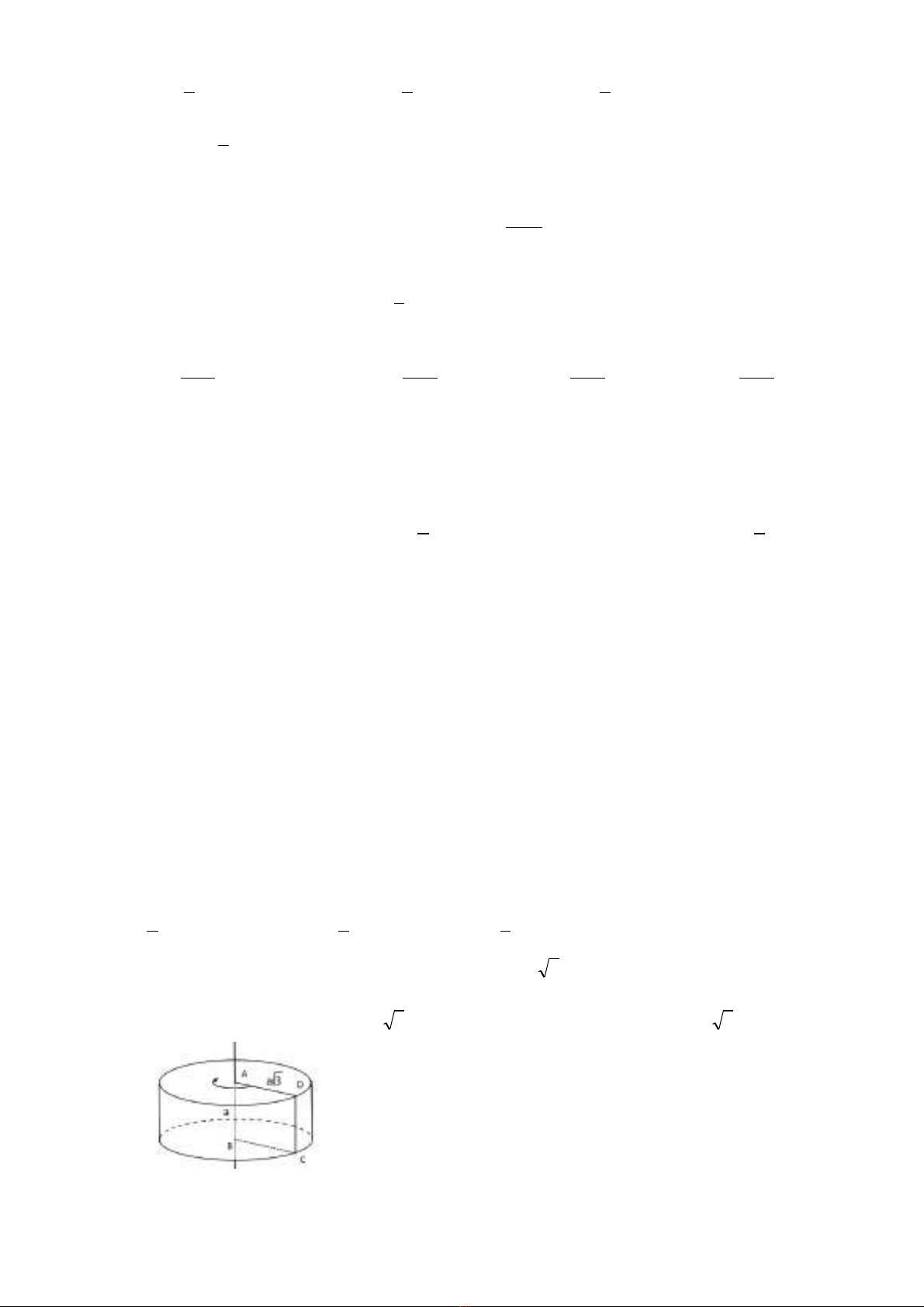
A.
1;
2
1
B.
1;
2
1
C.
;1
2
1
;
D.
;1
2
1
;
Câu 30. Cho
1log3log2log cbx aaa
. Khi đó x b ng ằ
A.
32 cab
B.
1
32 cb
C.
a
cb 32
D.
23cab
Câu 31. Giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
xx eey
2
trên đo n [-1ạ ;2]
A. 2e B.
3
1e
e
C.
1
2e
D.
2
e
Câu 32. N u ế
ba 7log;6log 1212
thì
A.
a
b
1
2log7
B.
a
b
1
2log7
C.
b
a
1
2log7
D.
b
a
1
2log7
Câu 33. N u hàm s ế ố
xx eey
2
4
thì
A.
012'13''' yyy
B.
yyy 12'13'''
C.
x
eyy 4
48'''''
D.
x
eyy 4
48'''''
Câu 34. T p nghi m c a b t ph ng trình ậ ệ ủ ấ ươ
252ln2ln 22 xxx
là :
A.
5;0
B.
5;2
2
1
;0
C.
;50;
D.
5;2
2
1
;0
Câu 35. M t giáo viên ti t ki m và c đu m i tháng đu g i s ti n 2 tri u đng vào m t ộ ế ệ ứ ầ ỗ ề ở ố ề ệ ồ ộ
ngân hàng A v i lãi kép là 0,5%/ tháng. Bi t lãi su t không thay đi trong quá trình g i. H i ớ ế ấ ổ ở ỏ
sau 2 năm ng i đó nh n đc bao nhiêu ti n lãiườ ậ ượ ề ? ( làm tròn đn hàng nghìn)ế
A. 3 118 000đB. 3 120 000đC. 51 118 000đD. 51 120 000đ
Câu 36. Kh i đa di n đu lo i ố ệ ề ạ
{ ; }p q
là kh i đa di n có?ố ệ
A.
p
c nh, ạ
q
m tặB.
p
m t, ặ
q
c nhạC.
p
m t, ặ
q
đnhỉD.
p
đnh, ỉ
q
c nhạ
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình ch nh t, ữ ậ
)(ABCDSA
. Tâm m t c uặ ầ
ngo i ti p hình chóp S.ABCD là ạ ế
A. Giao đi m c a 2 đng chéo AB và CD.ể ủ ườ C. Tr ng tâm tam giác SAC.ọ
B. Tr ng tâm tam giác SBD.ọD. Trung đi m c nh SC.ể ạ
Câu 38. Cho t di n OABC có OA,OB,OC vuông góc v i nhau t ng đôi m t. Khi đó th tíchứ ệ ớ ừ ộ ể
c a kh i t di n OABC b ngủ ố ứ ệ ằ
A.
OCOBOA ..
6
1
. B.
OCOBOA ..
2
1
. C.
OCOBOA ..
3
1
. D.
OCOBOA ..
.
Câu 39. Cho hình ch nh t ABCD có AB =a, AD =ữ ậ
3a
quay quanh c nh AD c a nó nhạ ủ ư
hình v . Di n tích xung quanh c a hình tròn xoay sinh ra b ngẽ ệ ủ ằ
A.
2
12 a
. B.
312 2
a
. C.
2
6a
. D.
32 2
a
.
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình ch nh t, AB =a, AC =2a. C nh bênữ ậ ạ
SA
(ABCD), SA=3a. Th tích kh i chóp S.ABCD b ngể ố ằ
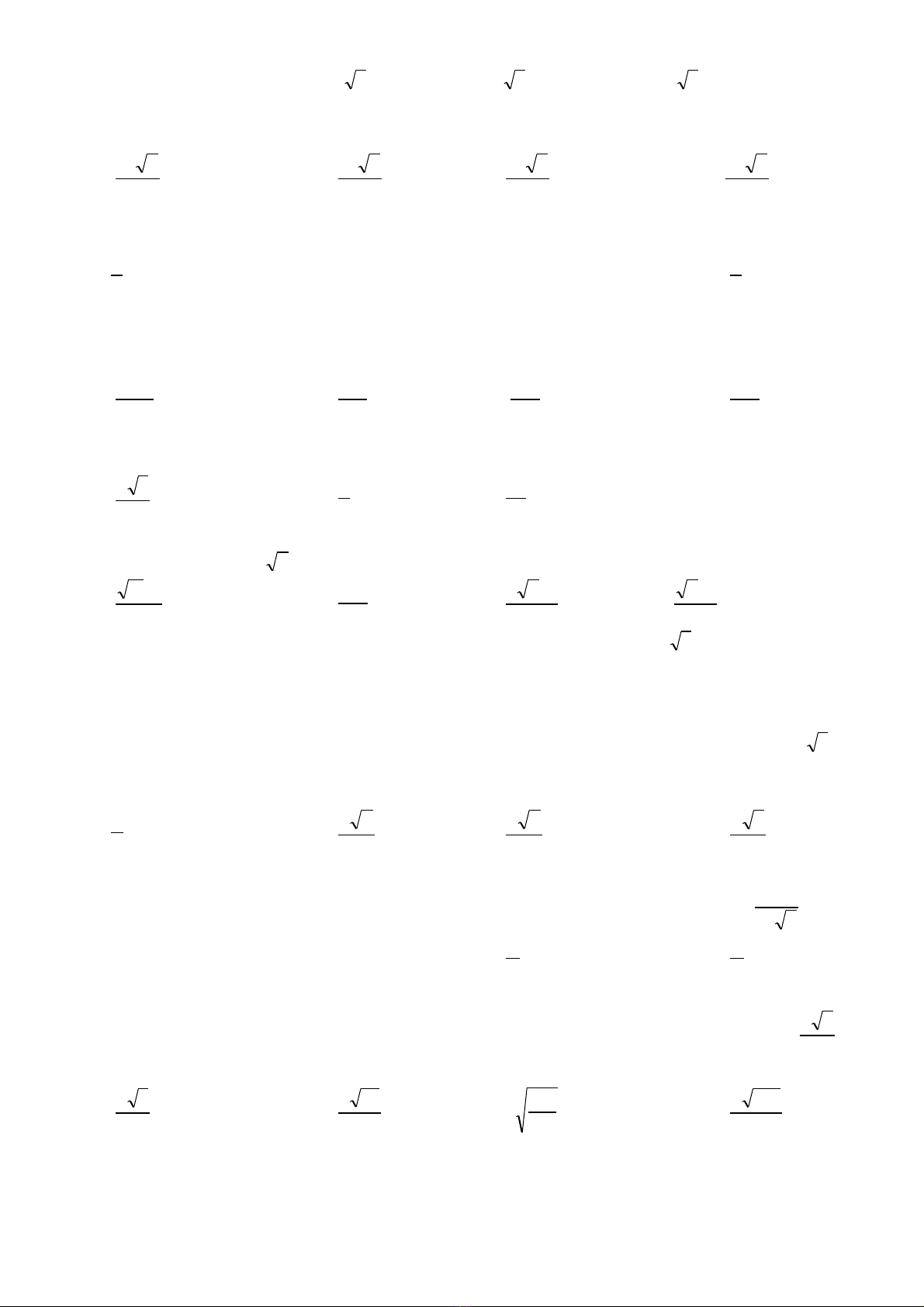
A.
3
.2 a
. B.
3
33 a
. C.
3
3a
. D.
3
5a
.
Câu 41. Cho kh i chóp t giác đu SABCD có t t c các c nh có đ dài b ng a. Tính th ố ứ ề ấ ả ạ ộ ằ ể
tích kh i chóp S.ABCố
A.
12
2
3
a
B.
2
2
3
a
C.
6
2
3
a
D.
3
2
3
a
Câu 42. Cho kh i t di n ABCD. G i B’, C’ l n l t là trung đi m c a SB, SC. Khi đó t số ứ ệ ọ ầ ượ ể ủ ỉ ố
th tích c a hai kh i chóp ABCD và AB’C’D b ng:ể ủ ố ằ
A.
2
1
B. 4 C. 2 D.
4
1
Câu 43. Cho hình lăng tr tam giác đu ABC.A’B’C’ có t t c các c nh đu b ng a. G i ụ ề ấ ả ạ ề ằ ọ
O,O’ l n l t là tâm c a đng tròn ngo i ti p 2 đáy. Tính th tích c a hình nón đc sinh ầ ượ ủ ườ ạ ế ể ủ ượ
ra khi quay tam giác O’OA quanh tr c OO’.ụ
A.
4
3
3
a
B.
3
3
a
C.
9
3
a
D.
4
3
a
Câu 44. Cho hình chóp tam giác đu SABC có c nh đáy b ng a, bi t (SBC) h p v i đáyề ạ ằ ế ợ ớ
(ABC) m t góc 60ộ0. Chi u cao c a kh i chóp SABC b ng:ề ủ ố ằ
A.
2
3a
B.
2
a
C.
2
3a
D.
a2
Câu 45. Cho hình chóp SABCD có ABCD là hình thang vuông t i A và D th a mãnạ ỏ
AB=2AD=2CD=2a=
2
SA và SA (ABCD). Khi đó th tích SBCD là:ể
A.
6
.2
3
a
B.
3
2
3
a
C.
3
22
3
a
D.
2
2
3
a
Câu 46. Cho hình chóp S.ABCD có đáy là hình ch nh t tâm ữ ậ I, AB =
a.32
, BC = 2a.
Chân đng cao ườ H h t đnh ạ ừ ỉ S xu ng đáy trùng v i trung đi m ố ớ ể DI. C nh bên ạSB t o v i ạ ớ
đáy góc 600. Th tích kh i chóp ể ố S.ABCD là:
A.
3
36a
B.
3
18a
C.
3
12a
D.
3
24a
Câu 47. Cho hình chóp S.ABCD có đáy ABCD là hình vuông c nh a tâm O, SA = ạ?
3
và
vuông góc v i (ABCD). G i G là tr ng tâm tam giác SAB. Kho ng cách t G đn m tớ ọ ọ ả ừ ế ặ
ph ng (SAC) là:ẳ
A.
2
a
B.
4
2a
C.
6
2a
D.
2
3a
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình vuông c nh b ng a, c nh ạ ằ ạ SA = 2a và
vuông góc v i đáy. Th tích kh i c u ngo i ti p hình chóp ớ ể ố ầ ạ ế S.ABCD là V. T s ỉ ố
6
3
a
V
là:
A.
B.
2
C.
2
D.
3
Câu 49. Cho hình chóp S.ABC có đáy là tam giác đu c nh a, góc gi a SC và mp(ABC) là 45ề ạ ữ
. Hình chi u c a S lên mp(ABC) là đi m H thu c AB sao cho HA = 2HB. Bi t CH=ế ủ ể ộ ế
3
7a
.Th tích hình chóp S.ABC và kho ng cách t H đn (SBC) b ng:ể ả ừ ế ằ
A.
6
3a
B.
12
14a
C.
139
21
a
D.
93
651a
Câu 50. Cho m t t m nhôm hình vuông c nh ộ ấ ạ
1
m nh hình v d i đây. Ng i ta c t ph nư ẽ ướ ườ ắ ầ
tô đm c a t m nhôm r i g p thành m t hình chóp t giác đu có c nh đáy b ng ậ ủ ấ ồ ậ ộ ứ ề ạ ằ
x
(m), sao