TRƯỜNG THCS
VĨNH THỊNH
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2017-2018
Môn: Toán - Lớp 7
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. Phần trắc nghiệm (2 điểm): Chọn chữ cái đứng trước câu trả lời đúng:
Câu 1: Bậc của đa thức 5 4 6 5 5 9 6 5 11
1
8 2 2 7 8
2
x y x y x y x y x
là:
A. 9 B. 11 C. 14 D. 5
Câu 2: Cho P(x) = -5x5 + 4x4 – x2 + x + 1; Q(x) = x5 – 5x4 + 2x3 + 1. Hiệu của
Q(x) - P(x) là:
A. -6x5 – 9x4 – 2x3 + x2 – 1; B. 6x5 – 9x4 + 2x3 + x2 – x;
C. 5x5 – 9x4 + 2x3 – x – 1; D. -4x5 + 9x4 + 2x3 + x2 – 1.
Câu 3: Cho tam giác ABC; BE và AD là hai trung
tuyến của tam giác; BE = 15cm. Số đo của BG là:
A. 5cm B. 9cm
C. 10cm D. 6cm
Câu 4: Cho tam giác ABC, khi đó ta có:
A. AB + AC < BC < AB – AC B. AB – AC < BC < AB + AC
C. AB + AC < BC < AB + AC D. AB – AC < BC < AB – AC
II. Phần tự luận:
Câu 5: Một đội bóng tham gia một giải bóng đá. Mỗi đội đều phải đá lượt đi và lượt về
với từng đội khác. Số bàn thắng trong các trận đấu của toàn giải được ghi lại trong bảng
sau:
Số bàn thắng (x) 0 1 2 3 4 5 6 7 8
Tần số (n) 10 13 15 20 11
9 3 4 5 N=90
a) Có tất cả bao nhiêu trận trong toàn giải?
b) Có bao nhiêu trận không có bàn thắng?
c) Tính số bàn thắng trung bình trong một trận của cả giải?
Câu 6: Cho đa thức: M(x) = 5x3 + 2x4 – x2 + 1 + 3x2 – x3 – x4 – 4x3
a) Thu gọn đa thức M(x).
b) Tính M(1) và M(-2).
c) Tìm nghiệm của đa thức M(x).
Câu 7: Số điểm tốt của ba tổ trong một lớp lần lượt tỉ lệ với 3; 4; 5. Biết tổ 1 ít hơn số
điểm tốt của tổ 3 là 10 điểm. Tính số điểm tốt của mỗi tổ.
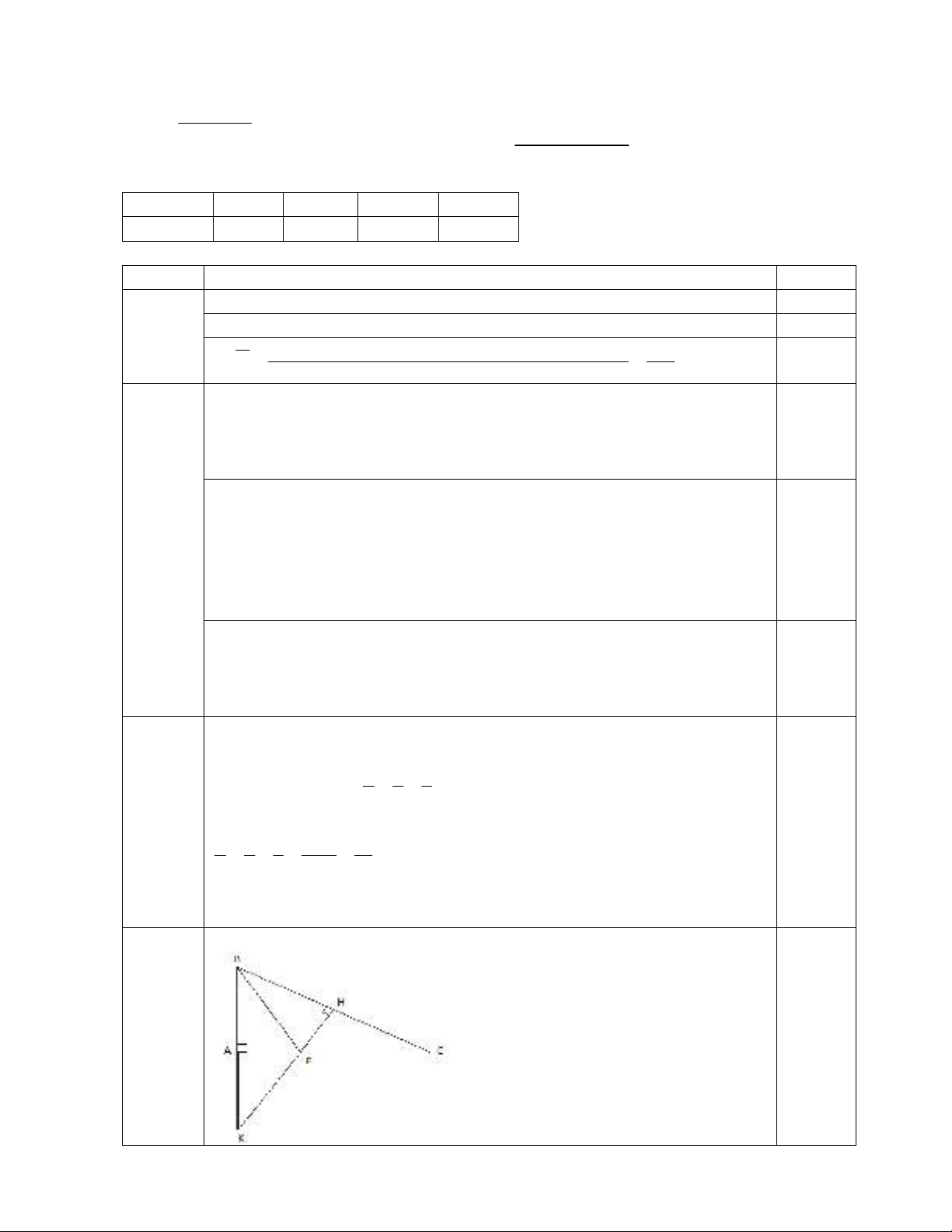
Câu 8: Cho tam giác ABC vuông tại A, đường phân giác BE. Kẻ EH
BC (H
BC).
Gọi K là giao điểm của AB và HE. Chứng minh rằng:
a)
ABE =
HBE
b) BE là đường trung trực của đoạn thẳng AH.
c) EK = EC
d) AE < EC.
Câu 9: Cho đa thức f(x) = ax2 + bx + c. Biết rằng giá trị của đa thức f(x) tại x = 0; x = 1
và x = -1 các số nguyên. Chứng minh rằng 2a; a + b và c là các số nguyên.
TRƯỜNG THCS
VĨNH THỊNH
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II
NĂM HỌC 2017-2018
Môn: Toán - Lớp 7
I. Phần trắc nghiệm: Mỗi câu đúng được 0,5 điểm.
Câu 1 2 3 4
Đáp án C B C B
II. Phần tự luận:
Câu Nội dung Điểm
5(1đ) a) Có 90 trận trong toàn giải. 0,25
b) Có 10 trận không có bàn thắng. 0,25
c) 0.10 1.13 2.15 3.20 4.11 5.9 6.3 7.4 8.5 278
3,09
90 90
X
0,5
6 (2đ) a) M(x) = 5x
3
+ 2x
4
– x
2
+ 1 + 3x
2
– x
3
– x
4
– 4x
3
= (5x3 – x3 – 4x3) + (2x4 – x4 ) + (3x2 – x2) + 1
= 0 + x4 + 2x2 + 1
= x4 + 2x2 + 1
0,25
0,25
b) M(1) = 1
4
+ 2.1
2
+ 1
= 1 + 2 + 1 = 4
Vậy M(1) = 4.
M(-2) = (-2)4 + 2.(-2)2 + 1
= 16 + 8 + 1 = 25.
Vậy M(-2) = 25
0,25
0,25
0,25
0,25
c) Ta có: x
4
0; x
2
0 với mọi x
R
Nên M(x) = x4 + 2x2 + 1
1 > 0.
Suy ra không có giá trị nào của x để M(x) = 0
Vậy đa thức M(x) không có nghiệm.
0,25
0,25
7 (1,5đ)
Gọi số điểm tốt của ba tổ lần lượt là a, b, c (a, b, c là số nguyên
dương).
Theo bài ra ta có:
3 4 5
abc
và c – a = 10
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
10
5
3 4 5 5 3 2
a b c c a
Suy ra: a = 15; b = 20; c = 25.
Vậy số điểm tốt của ba tổ lần lượt là 15 điểm, 20 điểm, 25 điểm.
1
0,5
8 (3đ) Vẽ hình, ghi giả thiết, kết luận đúng.
0,5
a)
ABE và
HBE có:
฀
฀
ABE HBE
(gt);
฀
฀
0
90
BAE BHE ;
BE là cạnh chung.
Suy ra:
ABE =
HBE (cạnh huyền – góc nhọn)
0,75
b) Vì
ABE =
HBE (theo phần a) nên:
AE = HE (hai cạnh tương ứng)
BA = BH (hai cạnh tương ứng)
AE = HE và BA = BH
BE là đường trung trực của đoạn thẳng
AH.
0,5
c)
AEK và
HEC có:
฀
฀
0
90
KAE CHE ;
AE = HE (cmt);
฀
฀
AEK HEK
(đối đỉnh).
Nên
AEK =
HEC (g.c.g)
Suy ra EK = EC (hai cạnh tương ứng).
0,75
d) Xét
AEK vuông tại A, có: AE < EK (quan hệ giữa góc và cạnh
đối diện trong một tam giác).
Mà EK = EC (cmt)
Suy ra AE < EC.
0,5
9 (0,5đ)
Từ f(0) = c
Z; f(1) = a + b + c
Z; f(-1) = a – b + c
Z
Do đó f(1) + f(-1) = 2a + 2c
Z, mà c
Z nên 2a
Z và a + b
Z.
Vậy 2a; a + b và c đều là số nguyên.
0,5