Đ 1Ề
Đ THI H C K II Ề Ọ Ỳ
Môn: Toán L p 8ớ
Th i gian: 90 phútờ
Đ BÀI Ề(Đ g m 05 câu)ề ồ
Câu 1: (3 đi m) Gi i các ph ng trình sau : ể ả ươ
a) 2x - 3 = 5 b) (x + 2)(3x - 15) = 0
c)
3 2 4 2
1 2 ( 1).( 2)
x
x x x x
−
− =
+ − + −
Câu 2: (1,5đi m) a) Gi i b t ph ng trình sau và bi u di n t p nghi m trên tr c s ể ả ấ ươ ể ễ ậ ệ ụ ố
2 2 2
2
3 2
x x+ −
< +
b) Tìm x đ giá tr c a bi u th c 3x – 4 nh h n giá tr c a bi u th c 5x – 6ể ị ủ ể ứ ỏ ơ ị ủ ể ứ
Câu 3: (2 đi m) M t ng i đi xe máy t Phú Thi n đn Pleiku v i v n t c 40 km/h. Lúc v ể ộ ườ ừ ệ ế ớ ậ ố ề
ng i đó u ng r u nên đi nhanh h n v i v n t c 70 km/h và th i gian v cũng ít h n th i ườ ố ượ ơ ớ ậ ố ờ ề ơ ờ
gian đi 45 phút. Tính quãng đng Phú Thi n t i Pleiku.ườ ệ ớ
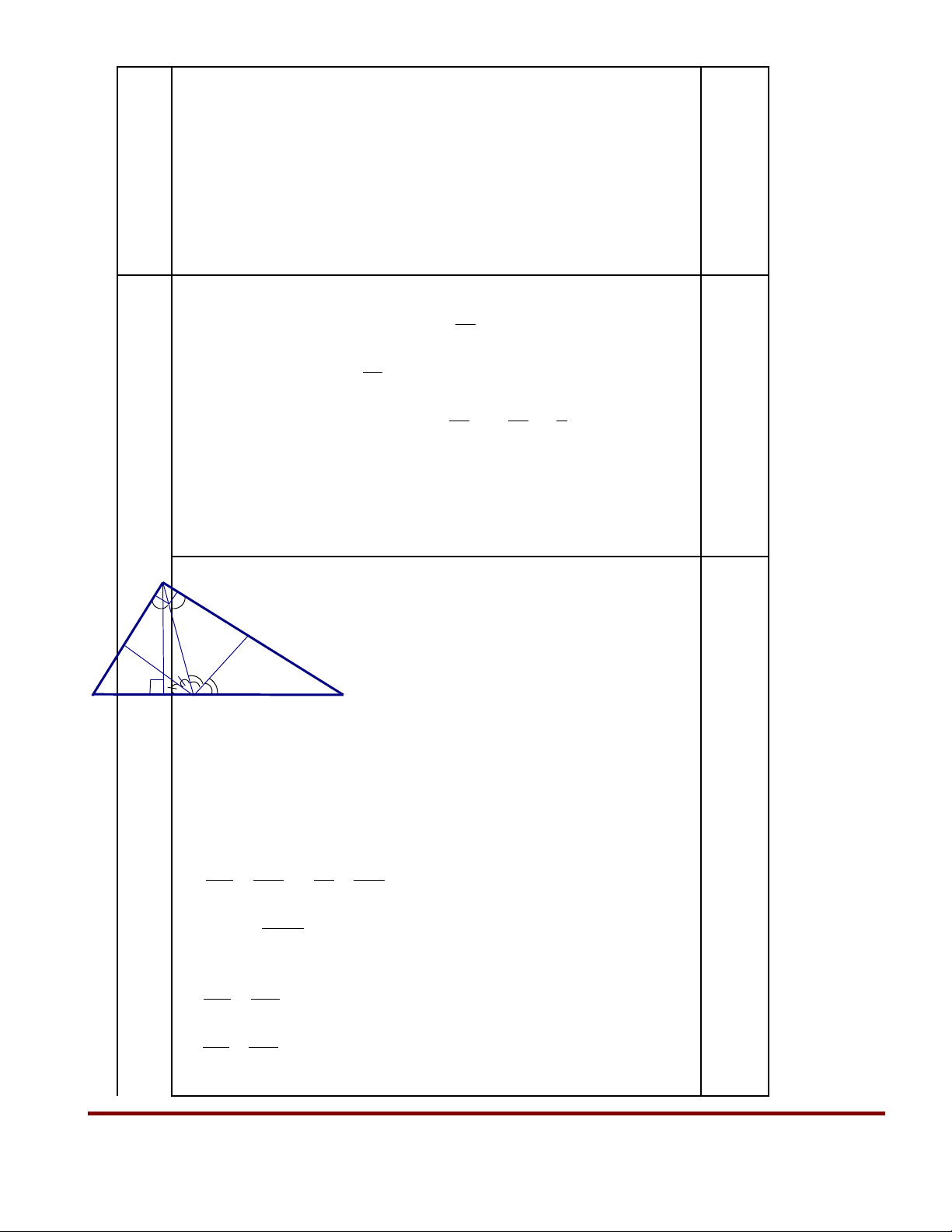
Câu 4: (4 đi m) ể Cho
∆
ABC vuông t i A, có AB = 12 cm ; AC = 16 cm. K đng cao AH Hạ ẻ ườ
BC).
a) Ch ng minh: ứ
∆
HBA ?
∆
ABC
b) Tính đ dài các đo n th ng BC, AH.ộ ạ ẳ
c) Trong
∆
ABC k phân giác AD (Dẻ
BC). Trong
∆
ADB k phân giác DE (Eẻ
AB); trong
∆
ADC k phân giác DF (Fẻ
AC).
Ch ng minh r ng: ứ ằ
EA DB FC 1
EB DC FA =� �
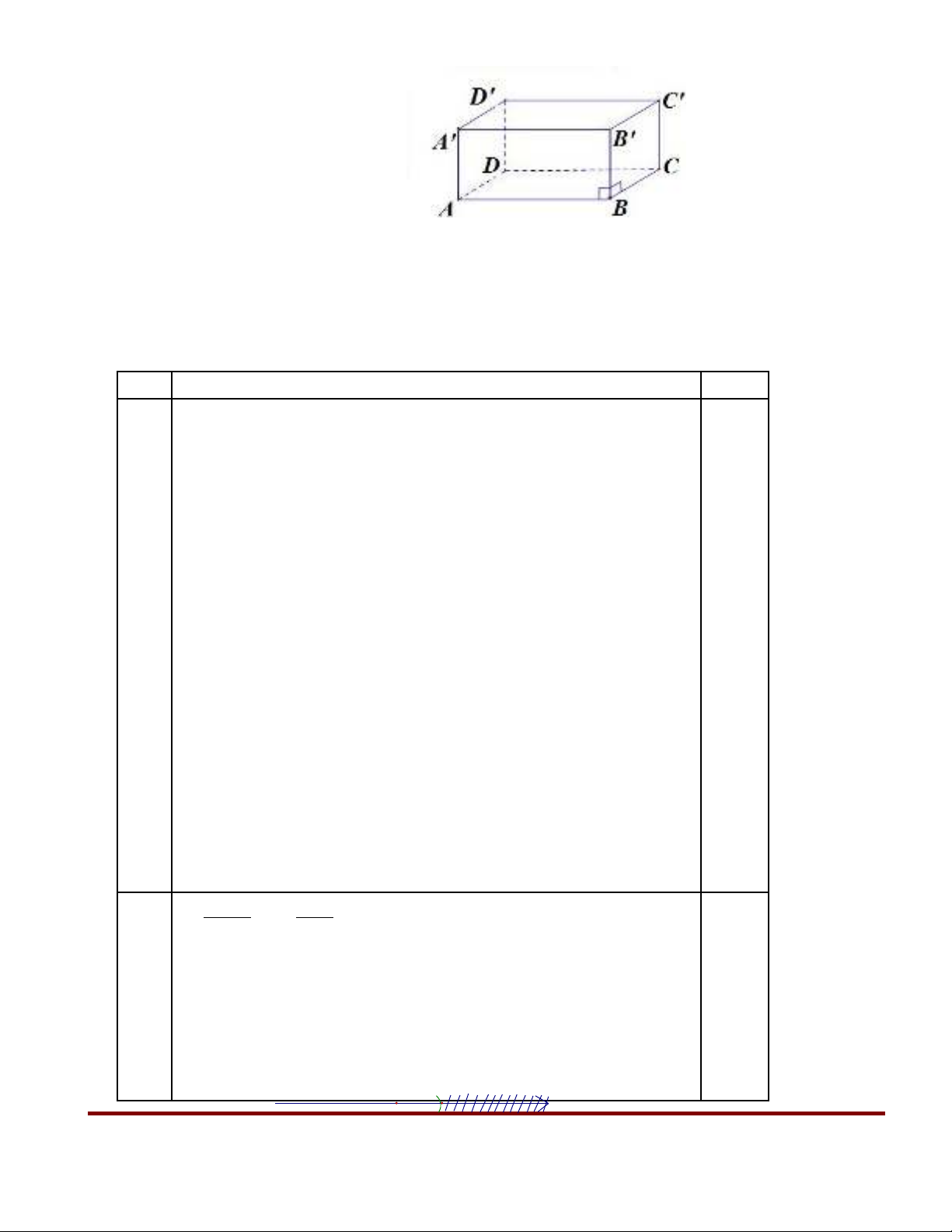
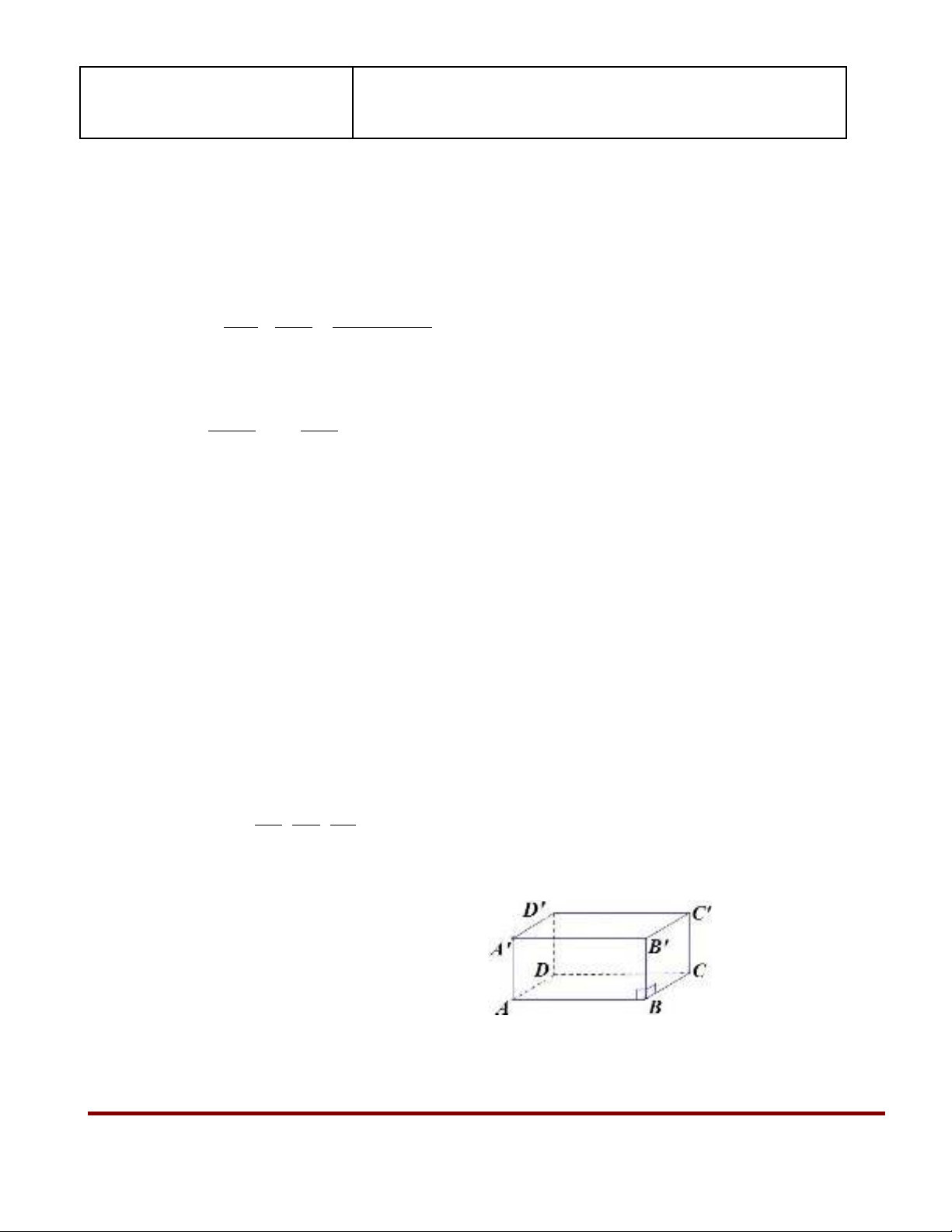
Câu 5: (0,5 đi m) ểTính th tích c a hình h p ch nh t ABCD.A’B’C’D’ trong ể ủ ộ ữ ậ
hình d i đây.ướ
Bi t: AB=5cm, BC=4cm, CC’=3cm ế
------------------H t----------------ế
KI M TRA H C KÌ II – TOÁN 8Ể Ọ
I. Khung ma tr nậ
Trang 1