ONTHIONLINE.NET
PHÒNG GD&ĐT TÂN KỲ ĐỀ THI KIỂM ĐỊNH CHẤT LƯỢNG MŨI NHỌN
Năm học 2010-2011
Môn thi: Toán 7
Thời gian: 120 phút (không kể thời gian giao đề)
Bài 1: (6 điểm)
a, Tính :
1 1 1 1 1 1 1
3 18 54 108 180 270 378
A
b, Tìm các số nguyên tố x, y sao cho : 51x+26y=2000
c, Tìm số tự nhiên n, biết: (214:1024).2n=128
Bài 2 ( 4,0 điểm )
Diện tích mảnh vườn hình chữ nhật là 108 m. Tính chiều dài, chiều rộng mảnh vườn đó
biết chúng lần lượt tỉ lệ với 4 và 3
Bài 3: (2,0 điểm)
Cho a,b,c
R và a,b,c
0 thoả mãn b2 = ac. Chứng minh rằng:
c
a =
2
2
( 2011 )
a b
b c
(Biết rằng các tỉ số đều có nghĩa)
Bài 4: (6,0 điểm)
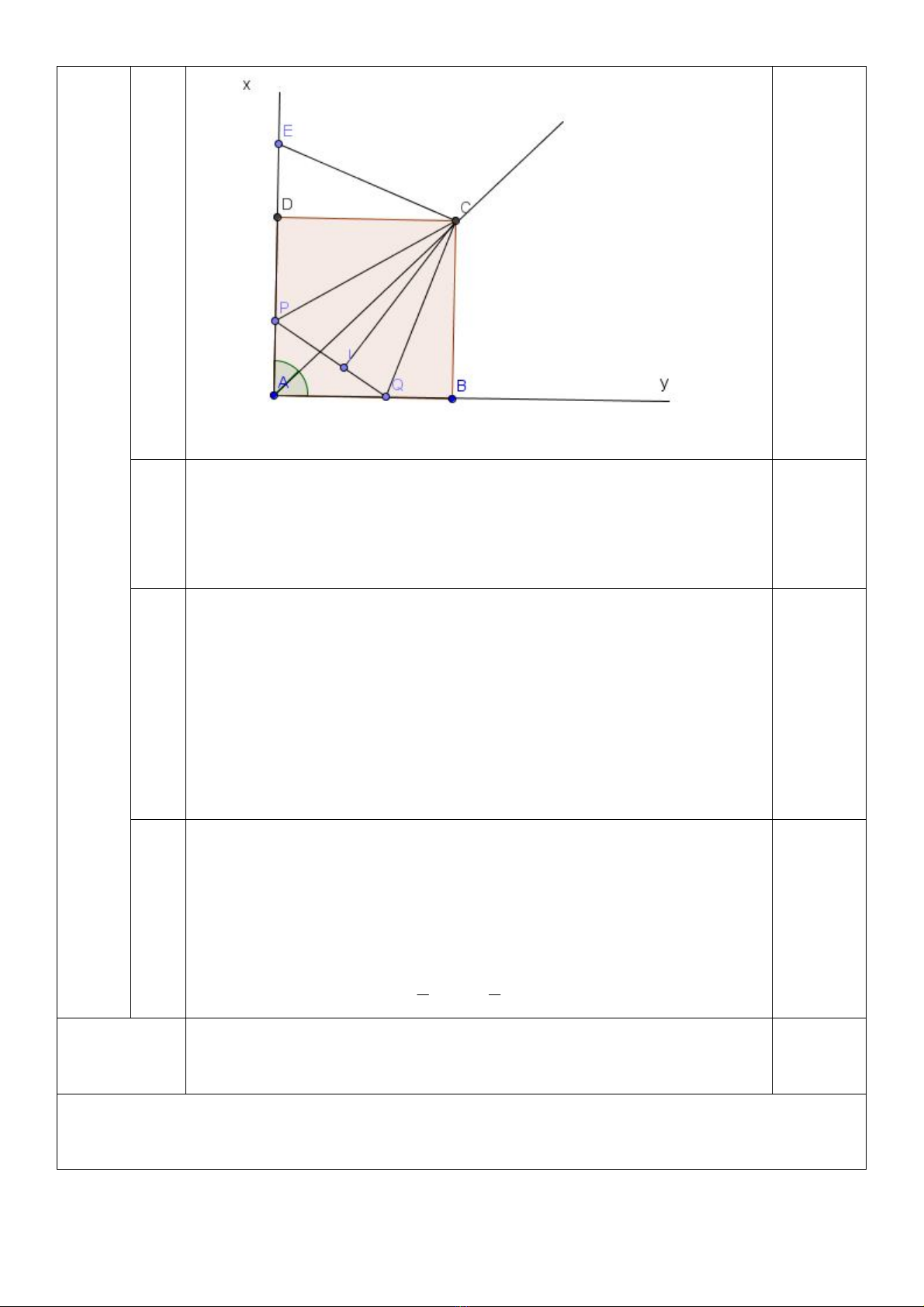
Cho góc vuông xAy. C là một điểm thuộc tia phân giác Az của góc xAy. D là hình chiếu
của C trên Ax, B là hình chiếu của C trên Ay. Trên các đoạn thẳng AD, AB lần lượt lấy
các điểm P, Q sao cho chu vi tam giác APQ bằng AD+AB. Trên tia Dx lấy điểm E sao cho
DE=QB. Chứng minh rằng:
a,
CDE=
CBQ
b, PC là tia phân giác của góc DPQ.
c, Góc PCQ có số đo bằng 450.
Bài 5: (2,0 điểm)
Cho đa thức f(x)= ax2+bx+c với a, b, c là các số thực thỏa mãn 13a+b+2c=0. Chứng tỏ
rằng: f(-2).f(3)
0
Hết./.
Đề chính thức
HƯỚNG DẪN CHẤM
Câu Nội dung cấn đạt Điềm
a,
2,0đ
1 1 1 1 1 1 1
3 18 54 108 180 270 378
1 1 1 1 1 1 1
( )
3 18 54 108 180 270 378
1 1 1 1 1 1 1
( )
3 3.6 6.9 9.12 12.15 15.18 18.21
1 1 1 1 1 1 1 1 1
( ... )
3 3 3 6 6 9 9 18 21
1 1 1 1 1 1 6 1 2 5
( ) .
3 3 3 21 3 3 21 3 21 21
A
A
A
A
A
0,5đ
0,5đ
0,5đ
0,5đ
b,
2,0đ
Ta có: 51x+26y=2000; 26x
M
2; 2000
M
2 suy ra 51x
M
2
mà 51 và 2 là hai số nguyên tố cùng nhau nên x
M
2.
Mặt khác x là số nguyên tố nên x=2
Do đó, ta có: 51.2+26y=2000=>y=73 là số nguyên tố
Vậy x=2; y=73
0,5đ
0,5đ
0,5đ
0,5đ
Bài 1
6,0đ
c,
2,0đ
(214:1024).2n=128
(214:210).2n=128
24.2n=27
24+n=27
4+n=7
n=3
0,5đ
0,5đ
0,5đ
0,25đ
0,25đ
Bài 2
4,0 điểm
Gọi a,b lần lượt là chiều dài và chiều rộng của mảnh vườn ta có:
4 3
a b
k
=>a=4k; b=3k
Diên tích mảnh vườn là: a.b=4k.3k=12k2=108
=> k2=9=>k=3
=>a=12;b=9
1,0đ
1,0đ
1,0đ
1,0đ
Bài 3
2,0điểm
b2 = ac=>
2011 2011
2011 2011
b a a b b a b a b
c b b c c b c b c
2
2011 2011 2011
. .
2011 2011 2011
a b a b a b a a b
b c b c b c c b c
Do đó:
c
a =
2
2
( 2011 )
a b
b c
0,75đ
1,0đ
0,25đ
0,25đ
a,
1,75
a, Xét
CDE và
CBQ, có:
DC=CB(T/c điểm thuộc tia phân giác)
µ
µ
0
90
D B
DE=QB(gt)
Do đó
CDE=
CBQ(c.g.c)
1,75đ
b,
2,0
b, Ta có : AP+PQ+AQ=AD+AB(GT)(1)
EP+AP+AQ=DP+AP+AQ+QB=AD+AB(2)
Từ (1)(2)=>EP=PQ
Xét
CEP và
CQP, có:
CP chung
CE=CQ(Cạnh tương ứng của hai tg bằng nhau
CDE=
CBQ)
EP=PQ(c/m trên)
Vậy,
CEP=
CQP(c.c.c)
=>
·
·
EPC CPQ
=>PC là tia phân giác của góc DPQ
0,5đ
1,0đ
0,5đ
Bài 4
6,0 đ
c,
2,0
c, Kẻ CI
PQ
Chứng minh được các cặp tam giác bằng nhau:
CDP=
CIP(Cạnh huyền-góc nhọn);
CBQ=
CIQ(Cạnh
huyền-Cạnh góc vuông)
Từ đó chứng minh được CP,CQ lần lượt là tia phân giác của các
góc DCI, ICB
Chứng minh được
· ·
0 0
1 1
.90 45
2 2
PCQ DCB
1,0đ
0,5đ
0,5đ
Bài 5
2,0điểm
Ta có: f(-2)=a.(-2)2+b(-2)+c=4a-2b+c;f(3)=a.32+b.3+c =9a+3b+c
=>f(-2)+f(3)=13a+b+2c=0=>f(-2)=-f(3)
=>f(-2).f(3)=-[f(3)]2
0
0,75đ
0,75đ
0,5đ
Lưu ý:
+, Bài 4: Nếu học sinh không vẽ hình thi không chấm điểm
+, Học sinh giải theo cách khác đúng, phù hợp với chương trình thì vẫn cho điểm tối đa
PHÒNG GD ANH SƠN
TRƯỜNG THCS TÀO SƠN
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2013 - 2014
MÔN: TOÁN 7
( Thời gian 120 phút không kể thời gian giao đề)
Câu 1:(2 điểm)
a) Thực hiện phép tính:
2
1 1 2 5 1
: :
2 2 3 3 2
b) Xác đinh a để đồ thị hàm số y = ax đi qua điểm M(-2;-8). Vẽ đồ thị hàm số
vừa tìm được.
Câu 2:(2 điểm) Tìm x biết:
a.
1 4 2
3,2
3 5 5
x
b. Tìm
x
biết 2 1
2 .3 .5 10800
x x x
Câu 3: (2 điểm) a. Số A được chia thành 3 số tỉ lệ theo
231
: :
5 4 6
. Biết rằng tổng các
bình phương của ba số đó bằng 24309. Tìm số A.
b. Cho
a c
c b
. Chứng minh rằng: 2 2
2 2
a c a
b c b
( Với thiết các biểu thức đều
có nghĩa)
Câu 4: (3 điểm) Cho tam giác ABC có
฀
0
A 90
, AB = AC. Qua A vẽ đường thẳng d
sao cho B và C nằm cùng phía đối với đường thẳng d. Kẻ BH và CK vuông góc với d.
Chứng minh rằng:
a. AH = CK
b. HK = BH + CK
Câu 5: (1 điểm) Chứng minh rằng:
2 2 2 2 2 2 2 2
3 5 7 19
A 1
1 .2 2 .3 3 .4 9 .10
----------------- Hết. -----------------
( Lưu ý: Cán bộ coi thi không giải thích gì thêm)
HƯỚNG DẪN CHẤM
Câu ý
Đáp án Điểm
1
a
2
1 1 2 5 1 1 9 13 8 13 16 39 23
: : :
2 2 3 3 2 2 16 6 9 6 18 18
1,0
b
Vì đồ thị đi qua điểm M(-2;-8) nên ta có: - 8 = a.( -2)
a = 4
Vậy hàm số đã cho là; y = 4x.
Chọn A(1;4). Nối OA ta có đồ thị hàm số y = 4x.
0,5
0.5
2
a
12
3
12
3
1 7
x = 2 + =
3 3
1 -5
x =-2 + =
3 3
1 4 2 1 4 16 2
3,2
3 5 5 3 5 5 5
1 4 14
3 5 5
12
3

x
x
x x
x
x
0.25
0.25
0.25
0.25
b
2
2 1
2 .3 .5 10800
2 .4.3 .3.5 10800
30 10800:12 900
30 30
2
xxx
x
x
x x x
x
0,25
0,25
0,25
0,25
3
a
Gọi a, b, c là ba số được chia ra từ số A.
Theo đề bài ta có: a : b : c =
231
: :
5 4 6
(1)
và a2 +b2 +c2 = 24309 (2)
0,25
4
2
-2
-4
-5
5
A