UBND THÀNH PHỐ KONTUM
PHÒNG GIÁO DỤC & ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP THÀNH PH
Ố
NĂM HỌC 2024-2025
- Môn: TOÁN HỌC – LỚP 9
- Thời gian: 150 phút (không kể thời gian giao đề)
- Ngày thi: 17/12/2024
(Đ
ề thi gồm
6
câu, 01 trang)
ĐỀ BÀI
Câu 1:(5,0 điểm)
1.1 Cho biểu thức
;
x x x
P x x
x x x x x
Rút gọn biểu thức
P
, tìm x để
P
1.2 Thực hiện phép tính:
29 12 5 29 12 5
1.3 Tìm các giá trị của x thoả mãn:
;
xx x
x
Câu 2:(5,0 điểm)
2.1 Cho
x y
. Chứng minh
x y
2.2 Giải phương trình sau:
x x x x x x
Câu 3:(3,0 điểm) Trong một giải bóng đá có 5 đội tham gia thi đấu thể thức vòng tròn một
lượt( hai đội bóng bất kỳ thi đấu với nhau đúng một trận). Sau mỗi trận đấu, đội thắng
được 3 điểm, đội thua không được điểm nào, còn nếu trận đấu có kết quả hoà thì mỗi đội
cùng được 1 điểm. Biết rằng tổng số điểm của tất cả các trận đấu của giải bằng 27 điểm.
Tính số trận hoà và số trận thắng của giải bóng đá đó.
Câu 4:(2,0 điểm)
Tung đồng thời hai con xúc xắc cân đối, đồng chất. Tính xác suất của mỗi biến cố sau:
A: ” Tổng số chấm thu được từ hai con xúc xắc bằng 7”
B: ” Tổng số chấm thu được từ hai con xúc xắc là số chính phương”
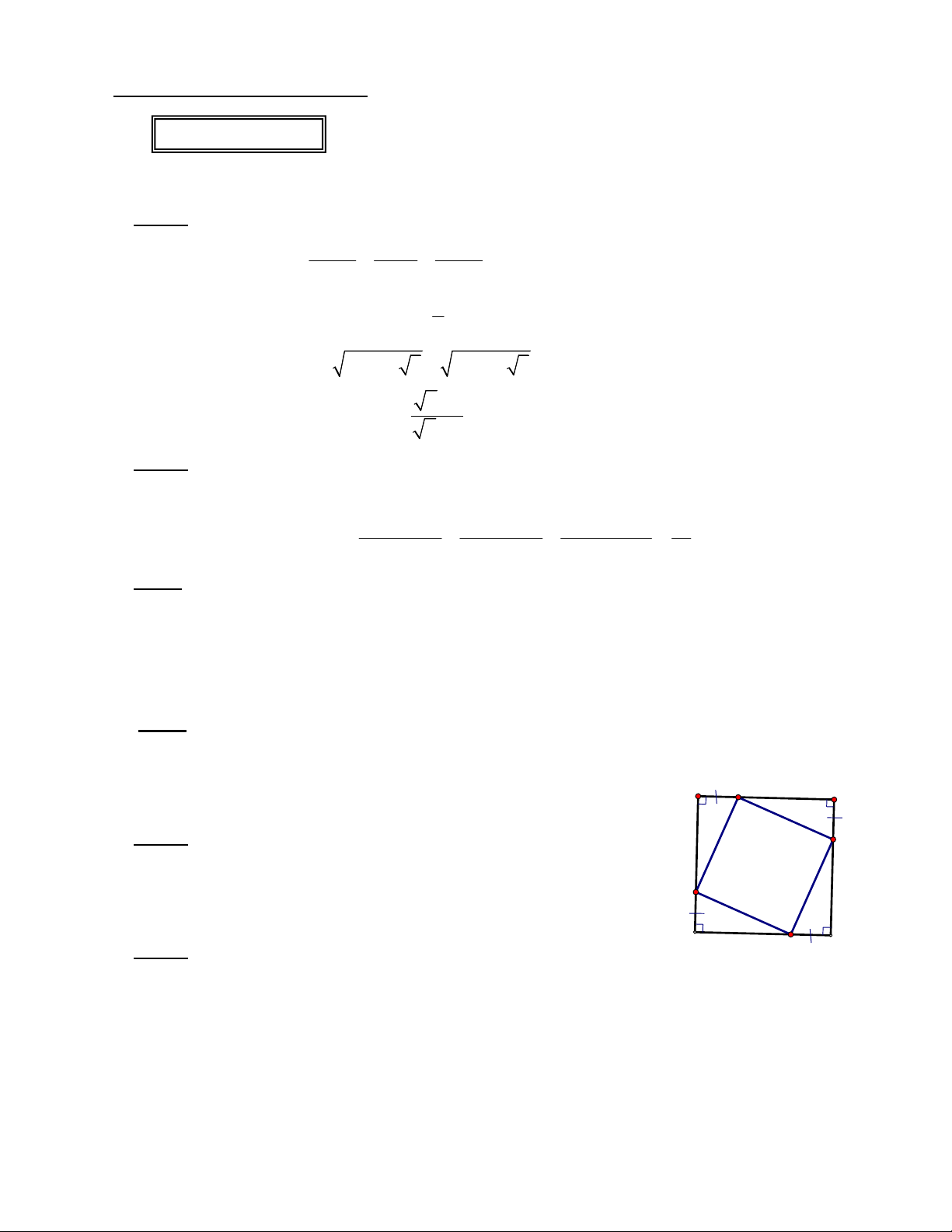
Câu 5: (3,0 điểm) Một mảnh vườn dạng hình vuông ABCD có cạnh
bằng 4m. Ở bốn góc vườn người ta trồng hoa hình dạng các tam giác
vuông bằng nhau(hình vẽ ). Hãy tính khoảng cách từ góc vườn A đến
vị trí M sao cho tứ giác MNPQ có chu vi nhỏ nhất.
Câu 6: (2,0 điểm)
Cho tam giác ABC nhọn. Chứng minh:
cot .cot cot .cot cot .cot
A B B C C A
------------------------------------------Hết---------------------------------------
- Thí sinh không được sử dụng tài liệu, máy tính cầm tay.
- Cán bộ coi thi không giải thích gì thêm.
Đ
Ề
CHÍNH TH
ỨC
D
C
A
B
M
N
P
Q


























