SÔÛ GIAÙO DUÏC ÑAØO TAÏO HAÄU GIANG
ÑEÀ THI HS GIỎI ÑBSCL MOÂN TOAÙN
(ĐỀ NGHỊ)
BAØI 1 (soá hoïc )
Cho
,a b Z
. Chöùng minh raèng :
Neáu 24a2 + 1 = b2 thì moät vaø chæ moät trong caùc soá a vaø b chia heát cho 5.
BAØI 2 (Ñaïi soá)
Tìm giaù trò nhoû nhaát cuûa haøm soá :
f(x) = 20x144 – 1.x120 + 2006, xIR.
BAØI 3 (Hình hoïc phaúng)
Cho tam giaùc ABC. Treân caïnh AB laáy ñieåm M di ñoäng, treân caïnh AC laáy
ñieåm N di ñoäng sao cho
1 1 1
AM AN l

(khoâng ñoåi).
Chöùng minh raèng ñöôøng thaúng MN ñi qua moät ñieåm coá ñònh.
BAØI 4 (Hình hoïc khoâng gian)
Trong maët phaúng (P) cho tam giaùc ABC nhoïn. Treân ñöôøng thaúng d vuoâng
goùc vôùi maët phaúng (P) taïi A laáy ñieåm S di ñoäng, goïi K vaø H laàn löôït laø
hình chieáu vuoâng goùc cuûa B leân AC vaø SC, ñöôøng thaúng l ñi qua K vaø H
caét ñöôøng thaúng d taïi N. Ñònh ñieåm S treân d sao cho ñoaïn SN ngaén nhaát.
BAØI 5 (daõy soá)
Cho daõy
*
nnN
u
vaø
(1). (3)... (2 1) , 1;2;3;...
(2). (4)... (2 )
n
f f f n
un
f f f n

Trong ñoù : f(n) = (n2 + n + 1)2 + 1
Chöùng minh raèng :
2
lim 2
n
nnu

ÑAÙP AÙN
Baøi 1 :
Neáu
5
5
a
b
,
khi ñoù töø ñaúng thöùc : 24a2 + 1 = b2 1 = b2 - 24a2 chia heát cho 5 =>
1 chia heát cho 5, voâ lyù.
Neáu
5 ( ,5) 1
5 ( ,5) 1
aa
bb



Khi ñoù : a4 1 (mod 5) (Ñònh lyù Fermat)
b4 1 (mod 5)
=> a4 - b4 0 (mod 5)
22
22
0 (mod 5)
0 (mod 5)
ab
ab


- Xeùt a2 + b2 0 (mod 5)
Töø ñaúng thöùc
voâ
lyù.
- Xeùt a2 - b2 0 (mod 5)
Töø ñaúng thöùc
2 2 2 2 2 2
24a + 1 = b 23a + 1 = (b - a ) 5 (23a + 1) 5ÛÞ
2
23a + 1 0(mod5)
, voâ lyù.
(Vì do (a,5)=1 => a ± 1 ; ± 2 (mod 5))
a2 1 ; 4 (mod 5) => 23a2 + 1 3 hoaëc 4 (mod 5)
Vaäy Neáu a,b Z thoûa ñaúng thöùc 24a2 + 1 = b2 thì moät vaø chæ moät trong
caùc soá a vaø b seõ chia heát cho 5.
BAØI 2
f(x) = 20x144 – 1.x120 + 2006
144 144 144 120
5 6 5 6 4 6
1 1 1
= 2.x + 2.x +...+2.x + + 2006
2 .12 2 .12 2 .12
x- + -
10 soá haïng
12 soá haïng
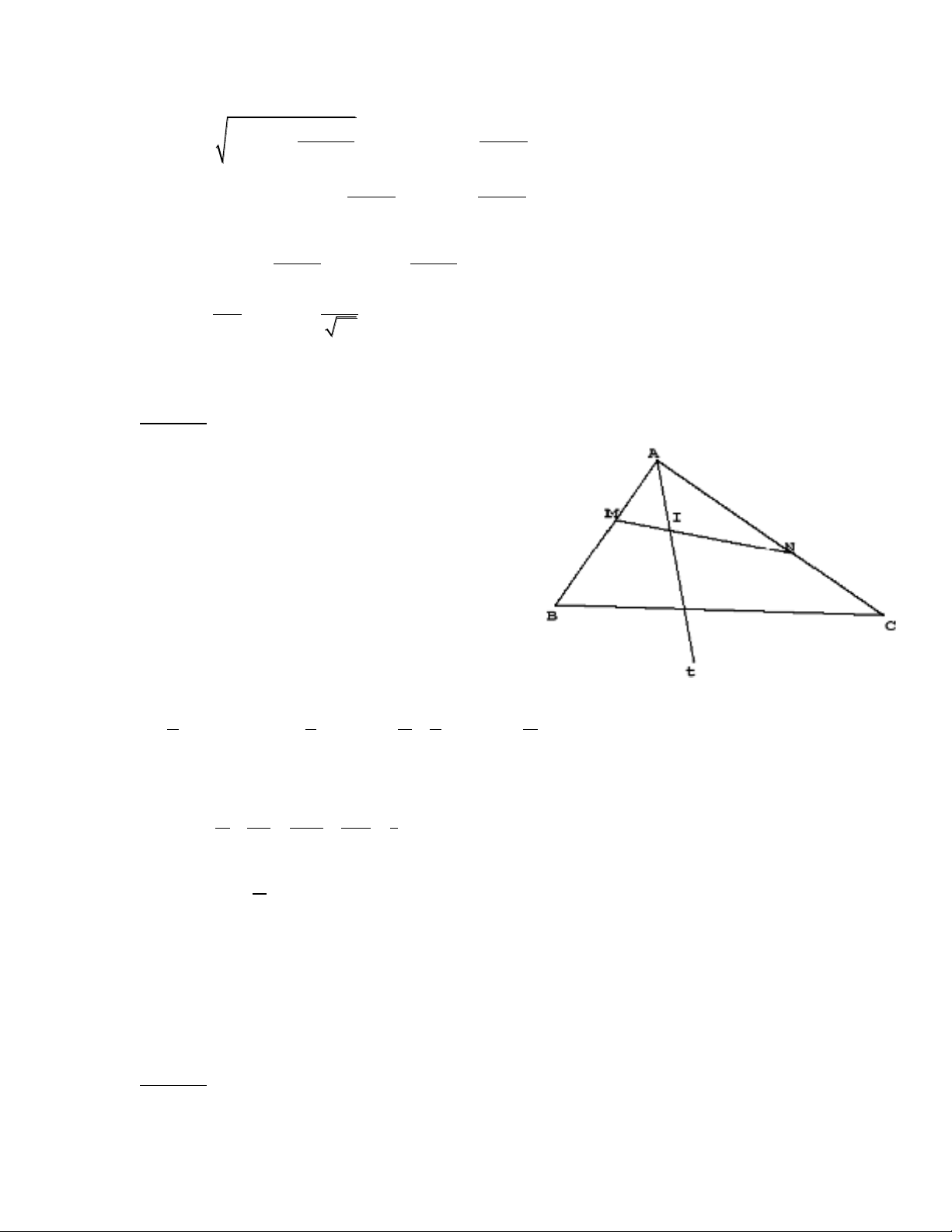
10 10.144 120
12
10 12 4 6
120 120
4 6 4 6
11
( ) 12 2 . . 2006
2 .12 2 .12
11
( ) 2006 2006
2 .12 2 .12
f x x x
f x x x






(Cosi)
144
4 6 5 6
144
624
11
( ) 2006 2.
2 .12 2 .12
11
()
24 24
f x x
x x do x R
BAØI 3 :
Keû ñöôøng phaân giaùc trong cuûa BAÂC laø
At. Do A,B,C coá ñònh => At coá ñònh.
Goïi I laø giao ñieåm cuûa At vôùi MN.
Ta coù : SAMN = SAMI + SANI
1 1 1
. .sin . . sin
2 2 2 2 2
AA
AM AN A AM AIsin AN AI
1 1 1 1
2 cos .
2
A
AI AM AN l



(khoâng ñoåi)
2 cos 2
A
AI l
(khoâng ñoåi)
=> I coá ñònh vaø I MN
Vaäy ñöôøng thaúng MN qua 1 ñieåûm coá ñònh I.
BAØI 4 :
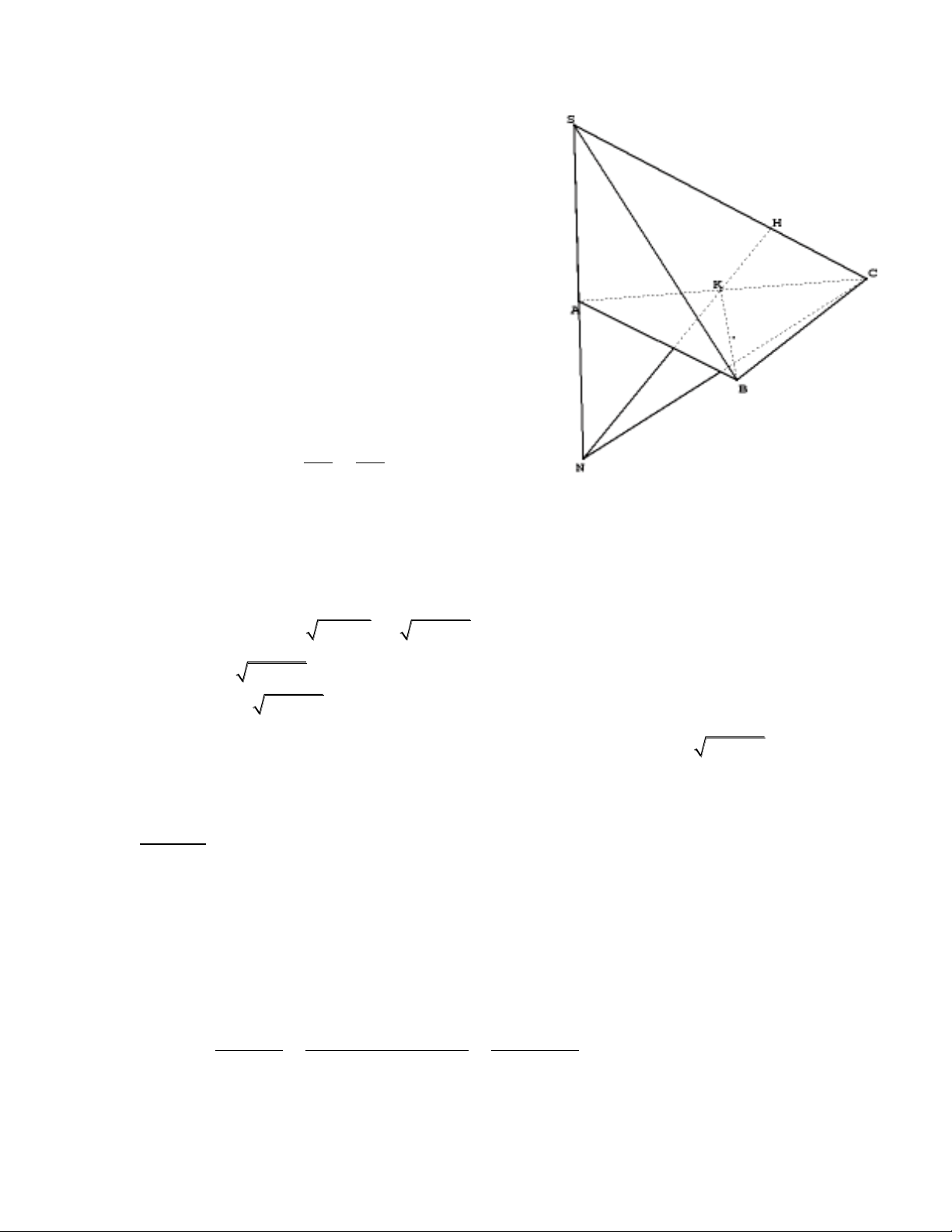
Trong SCN coù AC laø ñöôøng cao thöù
nhaát.
Maët khaùc ta coù :
()
SC BK SC BHK
SC BH

SC KH NH
laø ñöôøng cao thöù hai
=> K laø tröïc taâm cuûa SCN.
Ta coù
ANK . .D D Þ = Û =฀AN AK
ACS AS AN AK AC
AC AS
(khoâng ñoåi)
Vì
2 . 2 .SN SA AN SA AN AK AC
(khoâng ñoåi)
min 2.
.
SN AK AC
SA AN AK AC

Vaäy ñieåm S naèm treân d (coá ñònh) caùch A (coá ñònh) baèng :
.SA AK AC
BAØI 5 : Ta coù :
22
2
2
2
2 2 2
22
( ) ( 1) 1
( 1) 1
1 2 1 1
1 2 2
f n n n
nn
n n n n
n n n


Khi ñoù :
( )( )
( )( )
( )
( )
2
22
2
22
4 4 2 4 1 2 1 1
(2 1)
(2 ) 4 4 2 4 1 2 1 1
- + + -+
-==
+ + + ++
i i i i
fi
fi i i i i