ĐỀ THI MÔN BI N Đ I TÍN HI U SẾ Ổ Ệ Ố
Đề s : 061 - Th i gian: 45 phútố ờ
Cáu 1: Tín hi uệ
)n3(u)n(u −
là cách vi t khácế
c a tín hi u sau:ủ ệ
)3n()2n()1n()n( −δ+−δ+−δ+δ
)3n()1n()n( −δ+−δ+δ
)3n()2n()n( −δ+−δ+δ
)2n()1n()n( −δ+−δ+δ
Cáu 2: Ba m u đ u c a đáp ng xung c a hẫ ầ ủ ứ ủ ệ
nhân quả
)1n(x)n(x)1n(y4.0)n(y −−=−−
l n l t làầ ượ :
0 , 0.6 , - 0.24 0 , 0.6 ,
0.24
1 , - 0.6 , - 0.24 1 , 0.6 , 0.24
Cáu 3: Cho hai h th ng:ệ ố
(1)
)2n(x5)1n(x3)n(x2)n(y −−−+=
(2)
)2n(x5)1n(x3)n(x2)n(y 222 −−−+=
C hai đ u tuy n tínhả ề ế C hai đ u phiả ề
tuy n ế
Ch có h (2) tuy n tínhỉ ệ ế
Ch có h (1) tuy n tínhỉ ệ ế
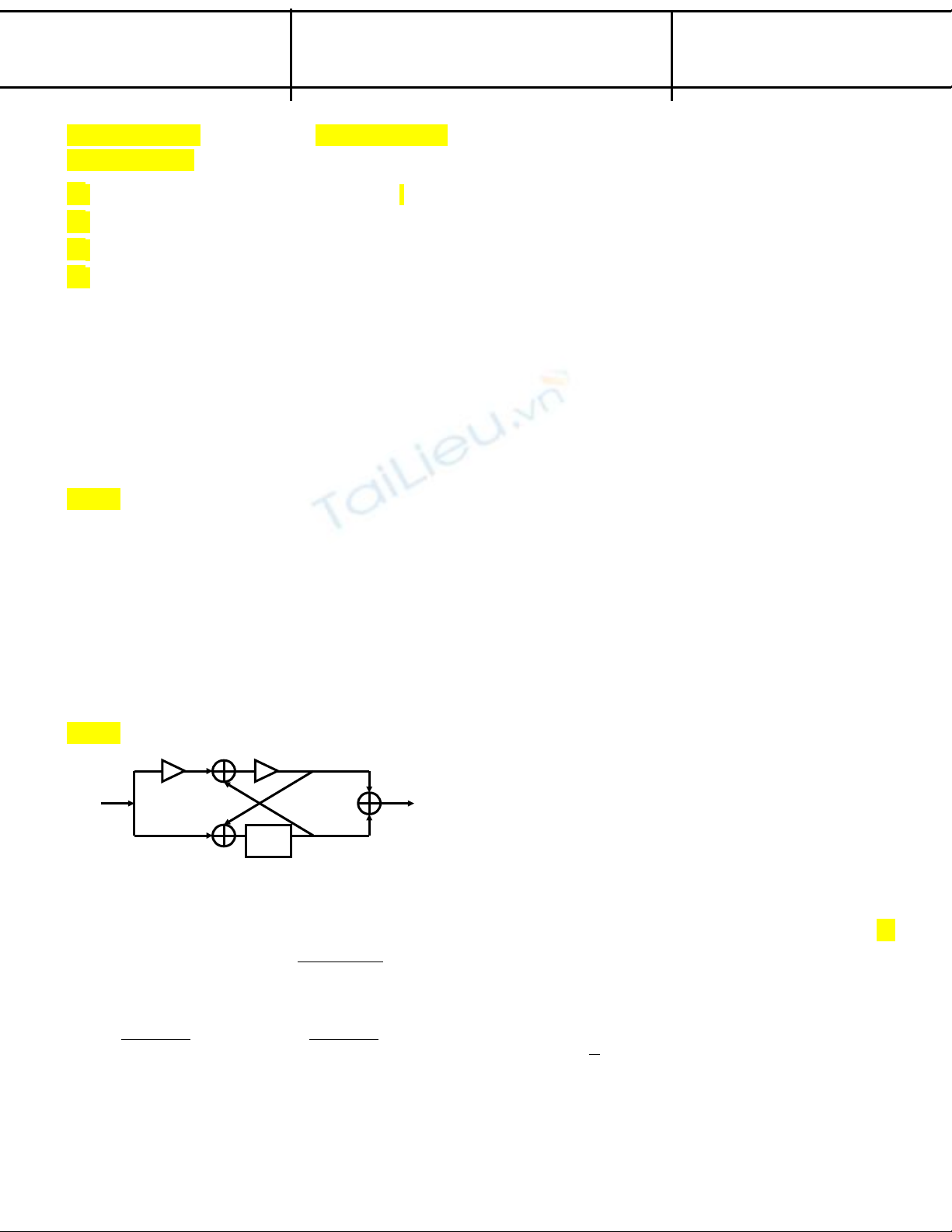
Cáu 4: Cho h th ng:ệ ố
Hàm truy n c a h này là:ề ủ ệ
a−
1
1
z1
aza
−
−
+
−
1
1
z1
aza
−
−
+
+
Cáu 5: Cho hai tên hiãûu
{ }
0,0,0,0,1,1,1,1)n(x1↑
=
vaì
{ }
1,1,0,0,0,0,1,1)n(x2↑
=
. Quan hãû giæîa X1(k)
vaì X2(k) laì:
)k(X)j()k(X 2
k
1=
)k(X)j()k(X 2
k
1−=
)k(X)1()k(X 2
k
1−=
)k(X)k(X 21 =
Cáu 6: Cho
{ }
7,6,5,4,3,2,1,0)n(x ↑
=
. Tæì
læu âäö thuáût toaïn FFT phán thåìi gian N = 8, suy
ra X(7) laì:
)WWW1(4 3
8
2
88 ++−−
)WWW1(4 3
8
2
88 −−−−
)WWW1(4 3
8
2
88 +−−−
)WWW1(4 3
8
2
88 +++−
Cáu 7: Tên hiãûu tæång tæû âæåüc láúy máùu våïi
táön säú 16 kHz räöi tênh DFT 512 máùu. Táön säú
(Hz) taûi vaûch phäø k = 127 laì:
0 31.25 3968.75
127
Cáu 8: B l c nhân qu :ộ ọ ả
y(n) - 0.2 y(n-1) = x(n) - x(n-2) có đáp ng xungứ
là:
)]2n(u)n(u[2.0
n
−−
)]2n(u)n(u[2.0
2n
−−
−
)]2n(u5)n(u[2.0
n
−−
)]2n(u25)n(u[2.0
n
−−
Cáu 9: Cho hai h th ng:ệ ố
(1)
[ ]
)2n(x)1n(x)n(x
3
1
)n(y −+−+=
(2)
)1n(y2.0)n(x)n(y −+=
-1
a
z - 1
ĐỀ THI MÔN BI N Đ I TÍN HI U SẾ Ổ Ệ Ố
Đề s : 061 - Th i gian: 45 phútố ờ
H (ệ1) không đ quy, h (2) đ quyệ ệ ệ
H (ệ1) đ quy, h (2) không đ quy ệ ệ ệ
Cả hai h đ u đ quy ệ ề ệ
C hai h đ u không đ quyả ệ ề ệ
Cáu 10: Cho tín hi u ệ
)n(u
4
n
cos π
đi qua b l cộ ọ
có đáp ng xung ứ
)2n(3)1n()n(2 −δ+−δ−δ
Tín hi u ra t i nệ ạ = 1 là:
0 0.41 1 -
0.41
Cáu 11: Cho
2
j
2j
j
e
2
1
1
e
)e(X
−
=ω−
ω−
ω
.
Đây là ph c a tín hi u sauổ ủ ệ :
)1n(u
2
1
)1n(
2n
−
−
−
)2n(u
2
1
)1n(
2n
−
−
−
Cả và đ u đúng ề Cả và đ uề
sai
Cáu 12: Cho
{ }
3,2,1,0)n(x 4↑
=
vaì caïc quan
hãû sau:
})n(y{DFT)k(X)k(Y};)n(x{DFT)k(X
4
2
4
===
Tên hiãûu
4
)n(y
laì:
}8,6,8,14{ ↑
}4,10,12,10{ ↑
}8,6,8,10{ ↑
}10,12,8,4{↑
Cáu 13: Cho tín hi u ệ
n
)1(
2
3
)n(x −=
n∀
đi qua
h th ng có ệ ố
)n(u)5.0()n(h n
=
. Tín hi u ra là:ệ
n
)1(−
n∀
n
)1(
2
3−
n∀
n
)1(
3
2−
n∀
2
3
n∀
Cáu 14: M t b l c s nhân qu t o tín hi u sinộ ộ ọ ố ả ạ ệ
t n s ầ ố
0
ω
có hàm truy n là:ề
1cosz2z
sinz
)z(H
0
2
0
+ω−
ω
=
Dùng b l c này đ t oộ ọ ể ạ
tín hi u sin ệ 2 kHz v i t n s l y m u ớ ầ ố ấ ẫ 8 kHz. Khi
tín hi u vào là xung dirac, tín hi u ra là: ệ ệ
)n(u)n
2
sin(π
)n(u)n
2
cos(π
)n
2
sin(π
)n
2
cos(π
Cáu 15: Cho tín hi u ệ
)n(u)
2
n
sin()n(u2 π
+
đi
qua h th ng FIR ệ ố
)1n(x5.0)n(x)n(y −+=
.
Tín hi u ra t i ệ ạ n = 1 là:
0 4 2
1
Cáu 16: Cho
1
z25.01
1
)z(X −
+
=
. Đây là bi nế
đ i Z c a hàm x[n] sau:ổ ủ
)n(u25.0 n
−
)n(u)25.0( n
−
Không có k t qu nàoế ả
đúng
Cáu 17: H sau:ệ
)2n(x)1n(y6.0)n(y −=−+
n đ nh Ổ ị Không nổ
đ nhị
Ch n đ nh khi h nhân quỉ ổ ị ệ ả
Cáu 18: Tên hiãûu tæång tæû âæåüc láúy máùu våïi
táön säú 44.1 kHz räöi tênh DFT våïi kêch thæåïc
cæía säø DFT laì 23.22 ms. Âäü phán giaíi cuía
DFT (tênh bàòng Hz) laì:
40.07 43.07 42.07
41.07
ĐỀ THI MÔN BI N Đ I TÍN HI U SẾ Ổ Ệ Ố
Đề s : 061 - Th i gian: 45 phútố ờ
Cáu 19: Cho tên hiãûu âi qua hãû thäúng loüc
phán chia hãû säú M = 2, âaïp æïng xung cuía bäü
loüc laì:
)3n(
4
1
)2n(
4
2
)1n(
4
3
)n()n(h
−δ+−δ+−δ+δ=
Tên hiãûu ra hãû thäúng trãn
)n(y 2H↓
laì:
)2n(
4
3
)1n(
4
9
)n( −δ+−δ+δ
)1n(
4
9−δ
)1n(
4
9
)n( −δ+δ
)2n(
4
3−δ
Cáu 20: Bäü loüc Haar coï âaïp æïng táön säú laì:
ω
+
j
e
2
1
2
1
ω−
+
j
e
2
1
2
1
ω
−
j
e
2
1
2
1
ω
−
j
e
2
1
2
1