1
TRƯỜNG THPT CHUYÊN VĨNH PHÚC
KỲ THI THỬ ĐẠI HỌC LẦN 1 NĂM HỌC 2012-2013
Môn: Toán 12. Khối A.
Thời gian làm bài: 150 phút (Không kể thời gian giao đề)
A.PHẦN CHUNG CHO TẤT CẢ THÍ SINH (8,0 điểm)
Câu I (2,5 điểm) Cho hàm số :
3
3 2
y x mx
= − +
(
)
1
,
m
lµ tham sè thùc.
1) Kh
ả
o sát s
ự
bi
ế
n thiên và v
ẽ
đồ
th
ị
hàm s
ố
(
)
khi
1
m
=
2) T×m c¸c gi¸ trÞ cña
m
®Ó ®å thÞ hµm sè
(
)
1
cã tiếp tuyến tạo với đường thẳng
: 7 0
d x y
+ + =
góc
α
,biết
1
cos
26
α = .
Câu II (2,5 điểm) 1) Giải phương trình :
4
3 4cos 2 8sin 1
sin 2 cos 2 sin 2
x x
x x x
− − =
+
2) Gi
ả
i h
ệ
ph
ươ
ng trình:
( )
3 3
2 2
4 16
1 5 1
x y y x
y x
+ = +
+ = +
( , )
x y
∈
R
.
Câu III (1,0 điểm) Tính giới hạn :
3 2
2
2
6 4
lim
4
x
x x
L
x
→
− − +
= −
Câu IV
. (1,0
đ
i
ể
m) Cho hình l
ậ
p ph
ươ
ng
1 1 1 1
.
ABCD A B C D
cã độ
dài c
ạ
nh b
ằ
ng
3
và
đ
i
ể
m
M
thu
ộ
c c
ạ
nh
1
2
CC
=
.M
ặ
t ph
ẳ
ng
(
)
α
đ
i qua
,A M
và song somg v
ớ
i
BD
chia kh
ố
i l
ậ
p ph
ươ
ng thành hai kh
ố
i
đ
a di
ệ
n.
Tính th
ể
tích hai kh
ố
i
đ
a di
ệ
n
đ
ó.
Câu V
. (1,0
đ
i
ể
m) Cho các s
ố
th
ự
c
, ,x y z
tho
ả
mãn
2 2 2
3
x y z
+ + =
. Tìm giá tr
ị
l
ớ
n nh
ấ
t c
ủ
a bi
ể
u th
ứ
c:
2 2
3 7 5 5 7 3
F x y y z z x
= + + + + +
B. PHẦN RIÊNG
(2,0 điểm). Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc 2)
1.Theo chương trình Chuẩn
Câu VIa.
( 1,0
đ
i
ể
m) Trong m
ặ
t ph
ẳ
ng v
ớ
i h
ệ
to
ạ
độ
Oxy
cho
hai ®iÓm
(
)
(
)
2;1 , 1; 3
A B
− −
vµ hai ®−êng
th¼ng
1 2
: 3 0; : 5 16 0.
d x y d x y
+ + = − − =
T×m to¹ ®é c¸c ®iÓm
,C D
lÇn l−ît thuéc
1 2
,d d
sao cho tø gi¸c
ABCD
lµ h×nh b×nh hµnh.
Câu VIIa. ( 1,0 điểm) Tính tổng :
2 1 2 2 2 3 2 2012
2012 2012 2012 2012
1 2 3 2012S C C C C= + + + +
⋯
2. Theo chương trình Nâng cao
Câu VIb. ( 1,0 điểm) Trong mặt phẳng hệ toạ độ
Oxy
cho e líp
( )
2 2
: 1
9 4
x y
E
+ =
vµ c¸c ®iÓm
(
)
3; 0
A − ;
(
)
1; 0
I − .T×m to¹ ®é c¸c ®iÓm
,B C
thuéc
(
)
E
sao cho
I
lµ t©m ®−êng trßn ngo¹i tiÕp tam gi¸c
ABC
Câu VII B:(
1,0 điểm): Tính tổng:
0 1 2 2012
2012 2012 2012 2012
1 2 3 2013
C C C C
T
= + + + +
⋯
-----------------------------------------------------------
HẾT
------------------------------------------------------
Ghi chú: - Thí sinh không được sử dụng bất cứ tài liệu gì!
- Cán bộ coi thi không giải thích gì thêm!
Đề chính thức
(Đề thi gồm 01 trang)
www.Vuihoc24h.vn - Kênh h󰹮c t󰹎p Online
Vuihoc24h.vn
2
TRƯỜNG THPT CHUYÊN VĨNH PHÚC
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC NĂM 2012-2013 – LẦN 1
MÔN TOÁN
– KHỐI A
(Đáp án gồm 5 trang)
Câu Nội dung trình bày Điểm
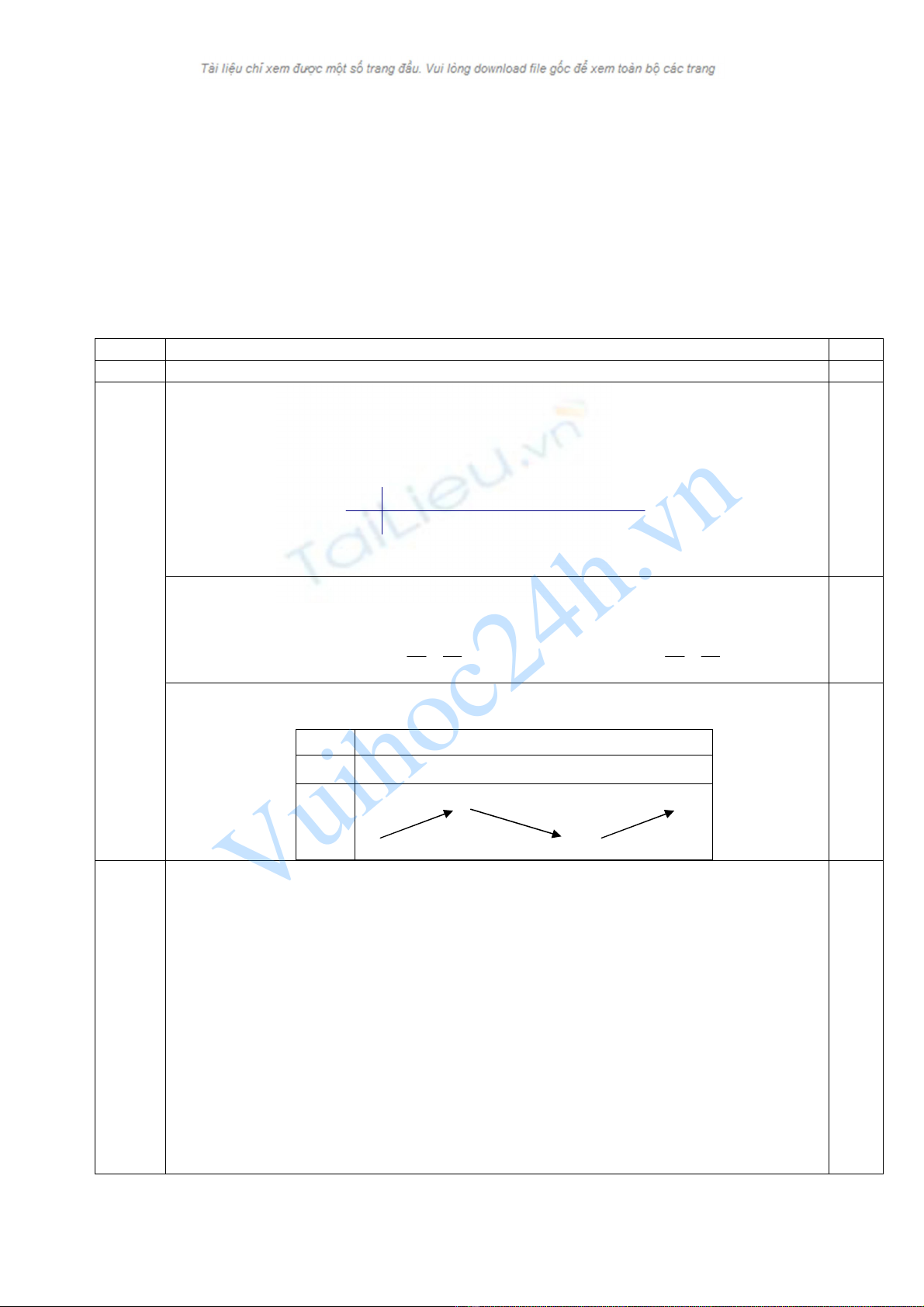
I(2,0đ) 1. (1,50 điểm)
Khi
1
m
=
hàm số (1) có dạng
3
3 2
y x x
= − +
a) Tập xác định
D
=
ℝ
b) Sự biến thiên
+) Chiều biến thiên:
2
' 3 3
y x
= −
,
' 0 1
y x
= ⇔ = ±
. Khi đó xét dấu của
'y
:
+ +
- 0
0
1-1 +∞∞∞
-∞∞∞
y
x
hàm số đồng biến trên khoảng
(
)
(
)
; 1 , 1;
−∞ − + ∞
và nghịch biến trên khoảng
(
)
1;1
− .
0,50
+) Cực trị: hàm số đạt cực đại tại
1, 4
CD
x y
= − =
Hàm số đạt cực tiểu tại
1, 0
CT
x y
= =
+) Giới hạn:
3 3
2 3 2 3
3 2 3 2
lim lim 1 ; lim lim 1
x x x x
y x y x
x x x x
→−∞ →−∞ →+∞ →+∞
 
= − + = −∞ = − + = +∞
 
0,25
+) Bảng biến thiên:
:
x
−∞
-1 1
+∞
y'
+
0
−
0
+
y
4
+∞
−∞
0
0,25
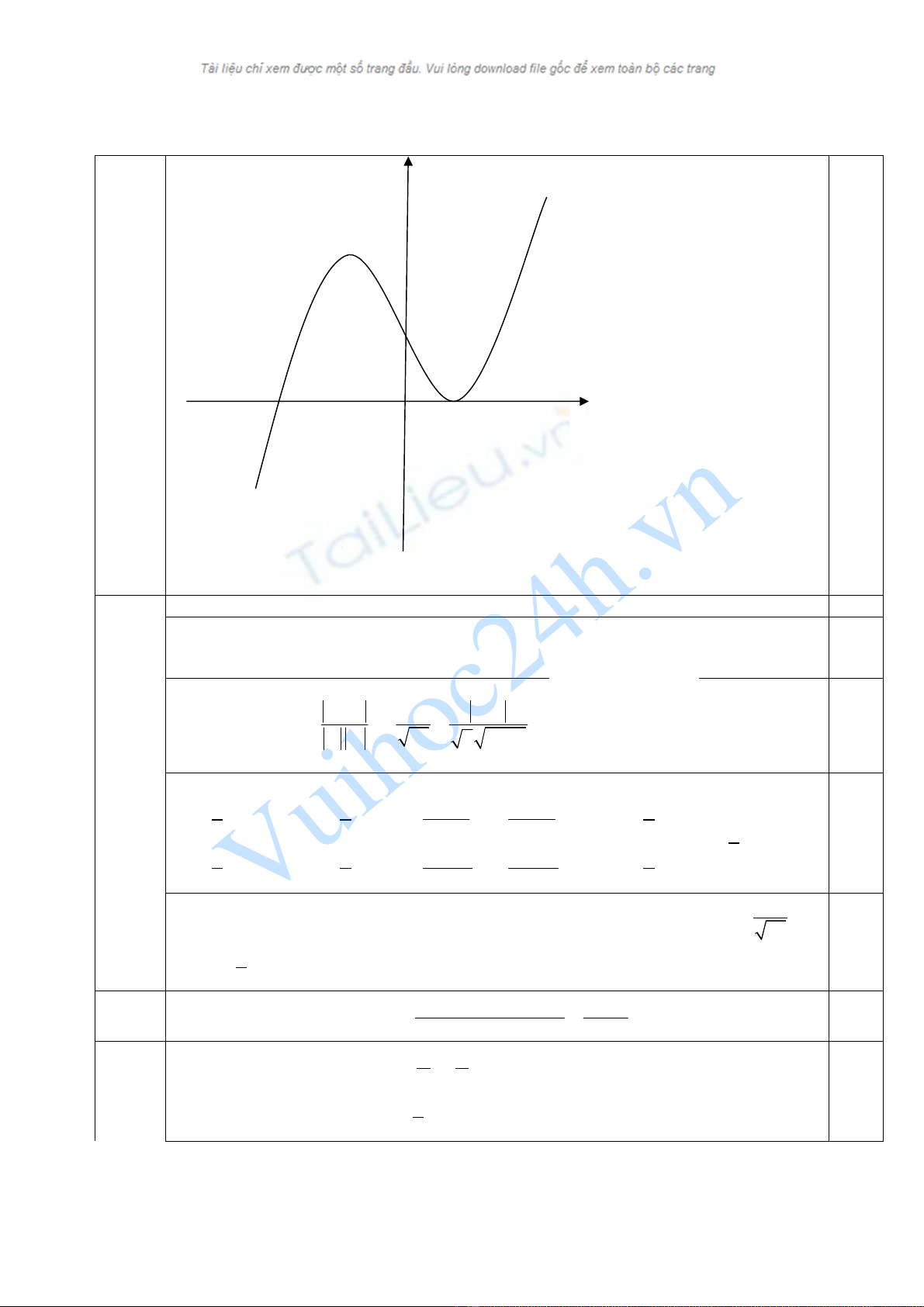
c) Đồ thị:
3
0 3 2 0 1, 2
y x x x x
= ⇔ − + = ⇔ = = −
, suy ra đồ thị hàm s
ố cắt trục Ox tại Ox
tại các điểm
(
)
(
)
1;0 , 2;0
−
'' 0 6 0 0
y x x
= ⇔ = ⇔ = ⇒
đồ thị hàm số nhận điểm
(
)
0;2
làm điểm uốn.
0,50
www.Vuihoc24h.vn - Kênh h󰹮c t󰹎p Online
Vuihoc24h.vn
3
2. (1,0 điểm)
Gọi
k
là hệ số góc của tiếp tuyến
⇒
tiếp tuyến có VTPT
(
)
1
; 1
n k
= −
Đườ
ng th
ẳ
ng
: 7 0
d x y
+ + =
ti
ếp tuyến có VTPT
(
)
2
1;1
n =
0,25
Ta có
( )
1 2
1 2 2
1 2
1
1
cos cos , 26
2 1
n n k
n n n n k
⋅ −
α = = ⇔ =
+

 
2
3 2
12 26 12 0
2 3
k k k k
⇔ − + = ⇔ = ∨ =
0,25
YCBT thoả mãn
⇔
ít nhất một trong hai phương trình sau có nghiệm:
, 2 2
, 2 2
3 3 2 1 2 1
3 3 0
2 2 2 2
2 2 9 2 9 2
3 3 0
3 3 9 9
m m
y x m x
m m
y x m x
+ +
= − = = ≥
⇔ ⇔ ⇔
+ +
= − = = ≥
1
2
2
9
m
m
≥ −
≥ −
1
2
m
⇔ ≥ −
0,25
V
ậy để đồ thị có tiếp tuyến tạo với đường thẳng
: 7 0
d x y
+ + =
góc
α
,có
1
cos
26
α = .
thì
1
2
m
≥ −
0,25
II(2,5đ)
1.(1,25 điểm).
Gi
ả
i ph
ươ
ng trình :
4
3 4cos 2
8sin 1
sin 2 cos 2 sin 2
x x
x x x
− − =
+
§/k
( )
sin 2 cos 2 0 8 2
sin 2 0
2
x l
x x l
x x l
π π
π
≠ − +
+ ≠
⇔ ∈
≠
≠
Z
0,25
1
-1
4
x
x
x
0
y
3
3 2
y x x
= − +
www.Vuihoc24h.vn - Kênh h󰹮c t󰹎p Online
Vuihoc24h.vn