www.MATHVN.com
Trêng THPT ®«ng s¬n i ®Ò thi thö ®¹i häc lÇn i n¨m häc 2012 – 2013
m«n to¸n . (Thêi gian lµm bµi 180 phót )
----------------------------------------------------
I. PH N CHUNG CHO T T C THÍ SINH Ầ Ấ Ả (7,0 đi m)ể
C©u I. (2,0 ®iÓm)
1. Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ (C) cña hµm sè:
23 3xxy −=
2. BiÖn luËn theo m sè nghiÖm cña ph¬ng tr×nh x =
xx
m
3
2−
C©u II. (2,0 ®iÓm)
1. Gi i ảbÊt ph ng trình: ươ
4)321)(13( 2≥−++−−+ xxxx
2. Gi i ph ng trình: ả ươ
)tan1(
cos
)2sin1(
).
4
sin(2 x
x
x
x+=
+
−
π
C©u III. (1,0 ®iÓm) T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó hµm sè y =
12
223
log 2
2
2++
++
mxx
xx
x¸c ®Þnh
Rx
∈∀
.
C©u IV. (1,0 ®iÓm) ) Cho h×nh chãp S.ABC , ®¸y ABC lµ tam gi¸c cã AB = 9;
AC = 12 . BC = 15. C¸c c¹nh bªn cña h×nh chãp b»ng nhau vµ b»ng 10.
TÝnh thÓ tÝch h×nh chãp S.ABC vµ thÓ tich h×nh cÇu néi tiÕp h×nh chãp
S.ABC
C©u V. (1,0 ®iÓm) Cho a, b,c d ng và ươ
3
222 =++ cba
. Tìm giá tr nh nh t c a bi uị ỏ ấ ủ ể
th cứ
II. PH N RIÊNGẦ (3,0 đi m)ểThí sinh ch đ c làm m t trong hai ỉ ượ ộ c©u (VIa ho c VIb).ặ
Câu VIa. (3,0 đi m)ể
1a.Trong m t ph ng ặ ẳ täa ®é Oxy, cho các đ ng th ng ườ ẳ
1
: 3 2 4 0d x y+ − =
;
2
: 5 2 9 0d x y− + =
.
Vi t ph ng trình đ ng tròn có tâm ế ươ ườ
2
I d
và ti p xúc v i ế ớ
1
d
t i đi m ạ ể
( )
2;5A−
.
2a. Gi i h ph ng trìnhả ệ ươ :
=++−
=
−
+− −
015)1(
0
1
log22 2
1
yyx
y
x
yx
3a. Mét tæ häc sinh cã 5 em N÷ vµ 8 em Nam ®îc xÕp thµnh mét hµng däc.
TÝnh x¸c suÊt ®Ó kh«ng cã hai em N÷ nµo ®øng c¹nh nhau.
Câu VIb. (2,0 đi m)ể
1b.Trong m t ph ng ặ ẳ täa ®é Oxy, cho ®êng trßn (C) : x2 + y2 - 6x - 2y + 1 = 0. ViÕt
ph¬ng tr×nh ®êng th¼ng (d) ®i qua M (0;2) vµ c¾t (C) theo d©y cung cã ®é dµi
b»ng 4.
2b.T×m hÖ sè cña
13
x
trong khai triÓn Niu t¬n ®a thøc
n
xxxxf 332 )12()
4
1
()( +++=
víi n lµ sè tù nhiªn tháa m·n:
nCA n
nn 14
23 =+ −
www.MATHVN.com
www.MATHVN.com
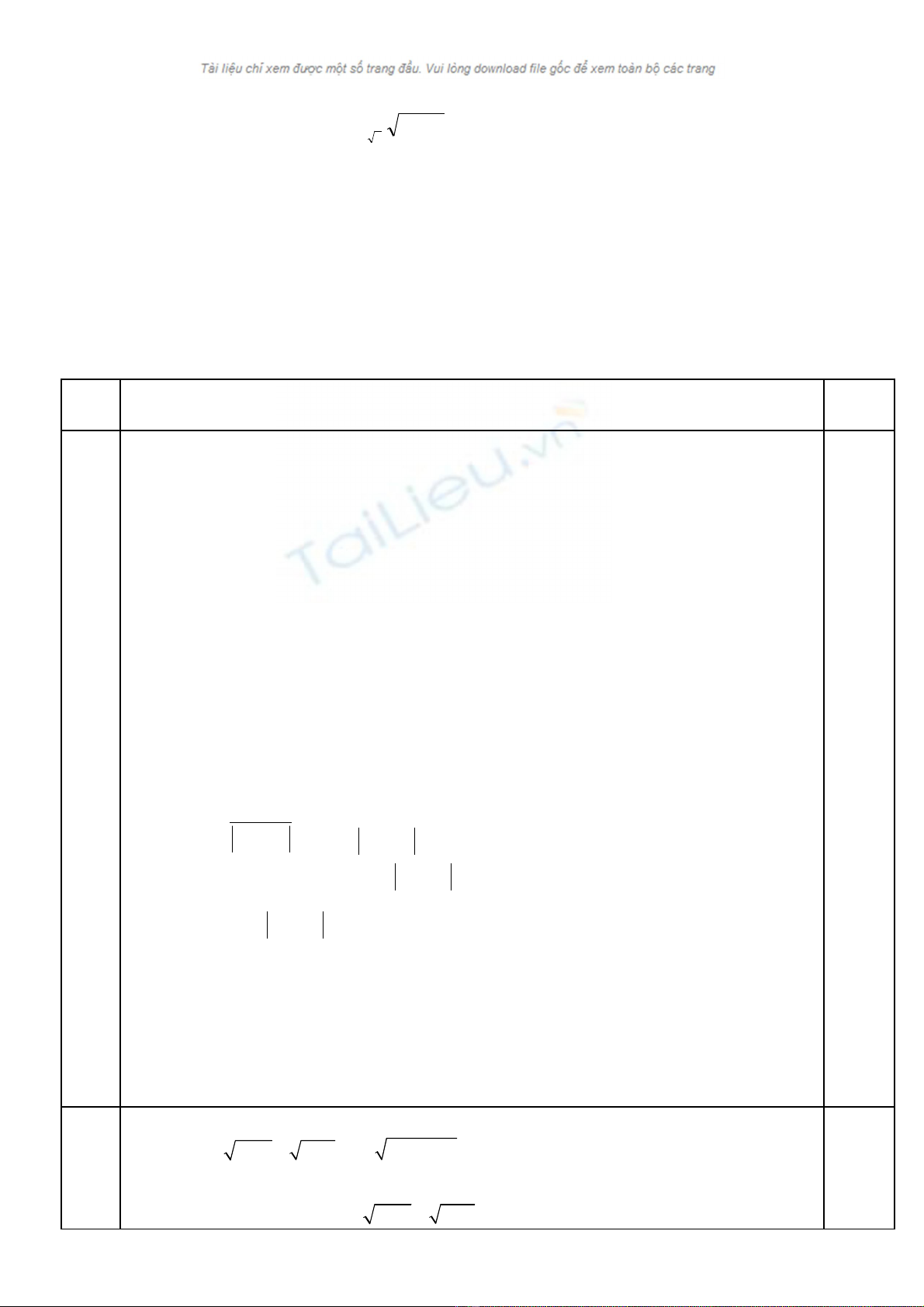
3b. Gi i h ph ng trình : ả ệ ươ
−−=+
=++−
1)24(log1log
136
32
8
2
2
2
yx
yxxyx
Hä vµ tªn thÝ sinh :--------------------------------------; Sè b¸o danh:-------
§¸p ¸n vµ thang ®iÓm
C©
u
§¸p ¸n §iÓ
m
C©
uI
1) y = x3 - 3x2.
* TËp x¸c ®Þnh : D = R
* Sù biÕn thiªn :
− Giíi h¹n:
lim
xy
+ = +
lim
xy
− = −
− ChiÒu biÕn thiªn : y, = 3x2 - 6x = 3x(x -2)
Hµm sè ®ång biÕn trªn c¸c kho¶ng ( -
; 0) vµ (2; +
), nghÞch biÕn
trªn kho¶ng (0;2).
- Đ th có đi m c c đ i (0;0), đi m c c ti u (2; -4)ồ ị ể ự ạ ể ự ể
− B¶ng biÕn thiªn ®óng
* §å thÞ :
y'' = 6x - 6 = 0
⇔
x = 1
§iÓm uèn U(1;-2) §å thÞ ®i qua c¸c ®iÓm (-1;−4), (3; 0) vµ nhËn
®iÓm U(1;-2) lµm t©m ®èi xøng .
vÏ ®óng ®å thÞ
2) +) x =
xx
m
3
2−
2
0, 3
3
x x
x x x m
− =
. Sè nghiÖm cña pt b»ng sè
giao ®iÓm cña ®å th y = ị
23x x x−
( x
0
và x
3) v i đ th y = m .ớồị
+) Ta có y =
3 2
2
3 2
3 0 3
33 0 3
x x khi x hoac x
x x x x x khi x
− < >
− = − + < <
.
+) b ng bi n thiên ả ế hoÆc vÏ ®å thÞ hµm sè ,
ta cã KQ:
m < 0 ho c m > 4 thì pt có 1 nghi m.ặ ệ
m = 0 pt vô nghi m.ệ
0 < m < 4 pt có 3 nghi m.ệ
m = 4 pt có 2 nghi m.ệ
0.25
0.25
0,25
0,25
0,25
0,25
0,25
0,25
C©
uII
1.(1®)
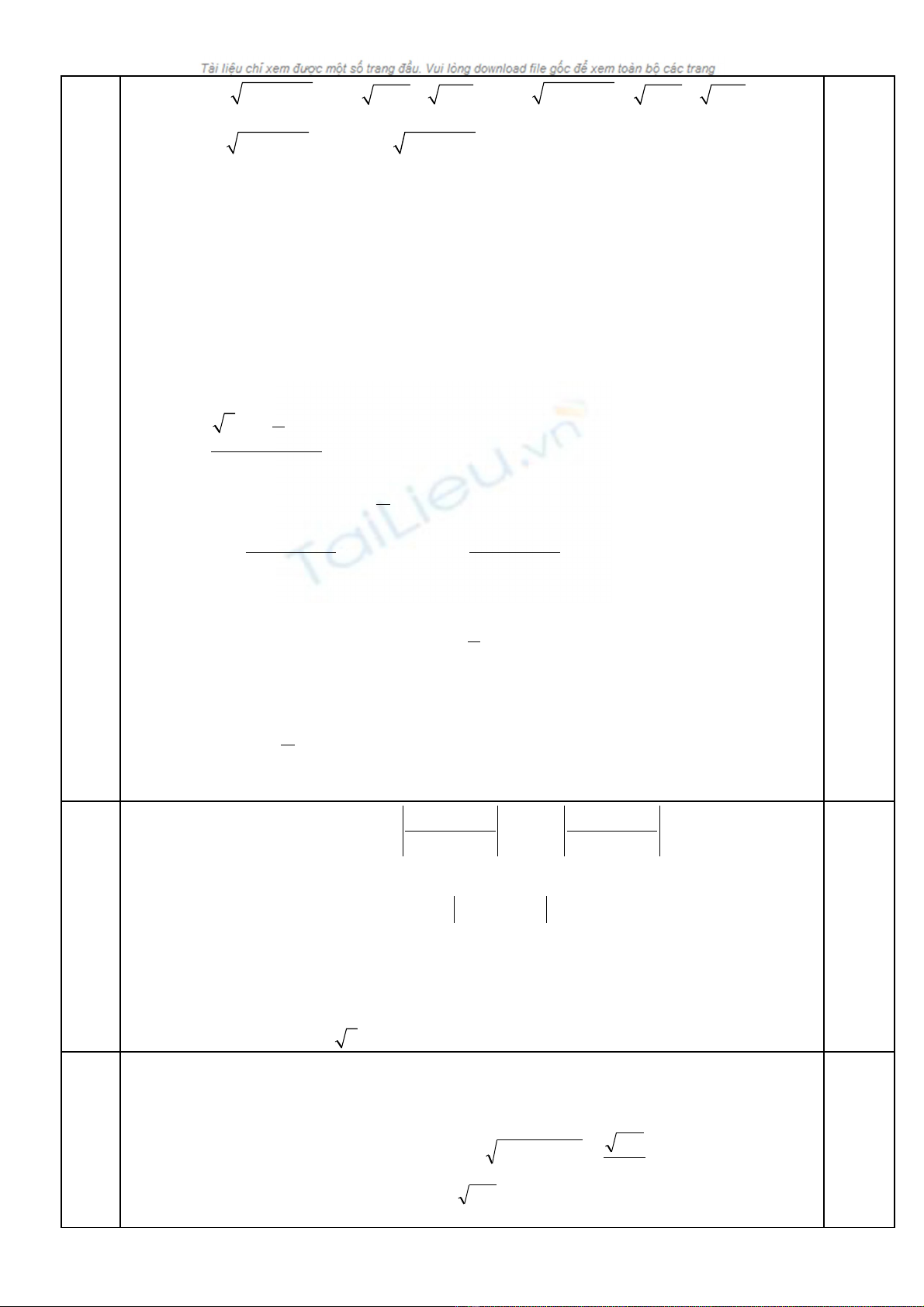
Gi i bpt: ả
( )
()
2
x 3 x 1 1 x 2 4+ − − + + x-3
Đi u ki n ề ệ
x 1
.
Nhân hai v c a bpt v i ế ủ ớ
x 3 x 1+ + −
, ta đ cượ 0,25
www.MATHVN.com
www.MATHVN.com
(1)
()
( )
2 2
4. 1 x 2 4. x 3 x 1 1 x 2 x 3 x 1x-3 x-3+ + + + − + + + + −� � � �
2 2 2 2
x 2 2 x 2 2 2 x 2 x x -2
x-2 x-3 x+2 x-3 - 4 0 x 2
+ + + + +� ۳�
K t h p v i đi u ki n ế ợ ớ ề ệ
x 1
ta đ c ượ
x 2
.
2(1®)
Gi i pt: ả
( )
2 sin x
41 sin 2x 1 tan x
cos x
π
� �
−
� �
� � + = +
Đi u ki n: .ề ệ
Rkkxx ∈+≠⇔≠ ;
2
0cos
π
π
Ta có (1)
( )
2
cos x sin x cos x sin x
cos x sin x
cos x cos x
− +
+ =�
( ) ( ) ( )
cos x sin x cos x sin x cos x sin x 1 0
� �
+ − + − =�� �
( ) ( )
cos x sin x cos 2 1 0x+ − =�
cos x sin x 0 tan x 1 x m , m
4
cos 2 1 0 cos 2 1 m
x x x
π
+ = = − = − + π
� �
� � � �
� �
− = =
� � = π
ﾢ
D th y h nghi m trên th a mãn đi u ki n. ễ ấ ọ ệ ỏ ề ệ
KQ:
Zkkxkx ∈=+−= ;;
4
ππ
π
0,25
0,2
5
0,25
0.25
0,25
0,25
0,25
C©
uIII Hµm s xác đ nh ố ị
2 2
22 2
3 2 2 3 2 2
log 0 1
2 1 2 1
x x x x
x R x R
x mx x mx
+ + + +
∀ ∀�۳۳ � + + + +
(*)
Vì 3x2 + 2x + 2 > 0
x∀
, nên (*)
2
2 2
1 0
2 1 3 2 2
m
x mx x x x
− <
+ + + + ∀
2
2
2 2(1 ) 1 0
4 2( 1) 3 0 ,
1 1
x m x
x m x x R
m
+ − +
+ + + ∀� � �
− < <
⇔
<<−
≤∆
≤∆
11
0
0
2
'
1
'
m
Gi i ra ta có v i : 1 - ả ớ
2 1m <
thì hàm s xác đ nh v i ố ị ớ
x R∀
.
0,25
0,25
0,25
0,25
C©
uIV
+) Ta thÊy tam gi¸c ABC vu«ng t¹i A
+) Gäi H lµ ch©n ®êng cao cña h×nh chãp, ta c/m ®îc: HA = HB =
HC = R lµ b¸n kÝnh ®êng trßn ngo¹i tiÕp tam gi¸c ABC suy ra H lµ
trung ®iÓm c¹nh BC nªn
2
175
2
2=−== HBSASHh
. TÝnh ®îc diÖn
tÝch ®¸y S = 54 suy ra V =
1759
0.25
0,25
www.MATHVN.com