Đ THI TH Đ I H C, CAO Đ NG Ề Ử Ạ Ọ Ẳ
Môn thi : TOÁN (Đ 181 )Ề
I. PH N CHUNG CHO T T C THÍ SINH Ầ Ấ Ả (7,0 đi m)ể
Câu I (2,0 đi m)ể Cho hàm số
2 1
1
x
yx
+
=+
(C)
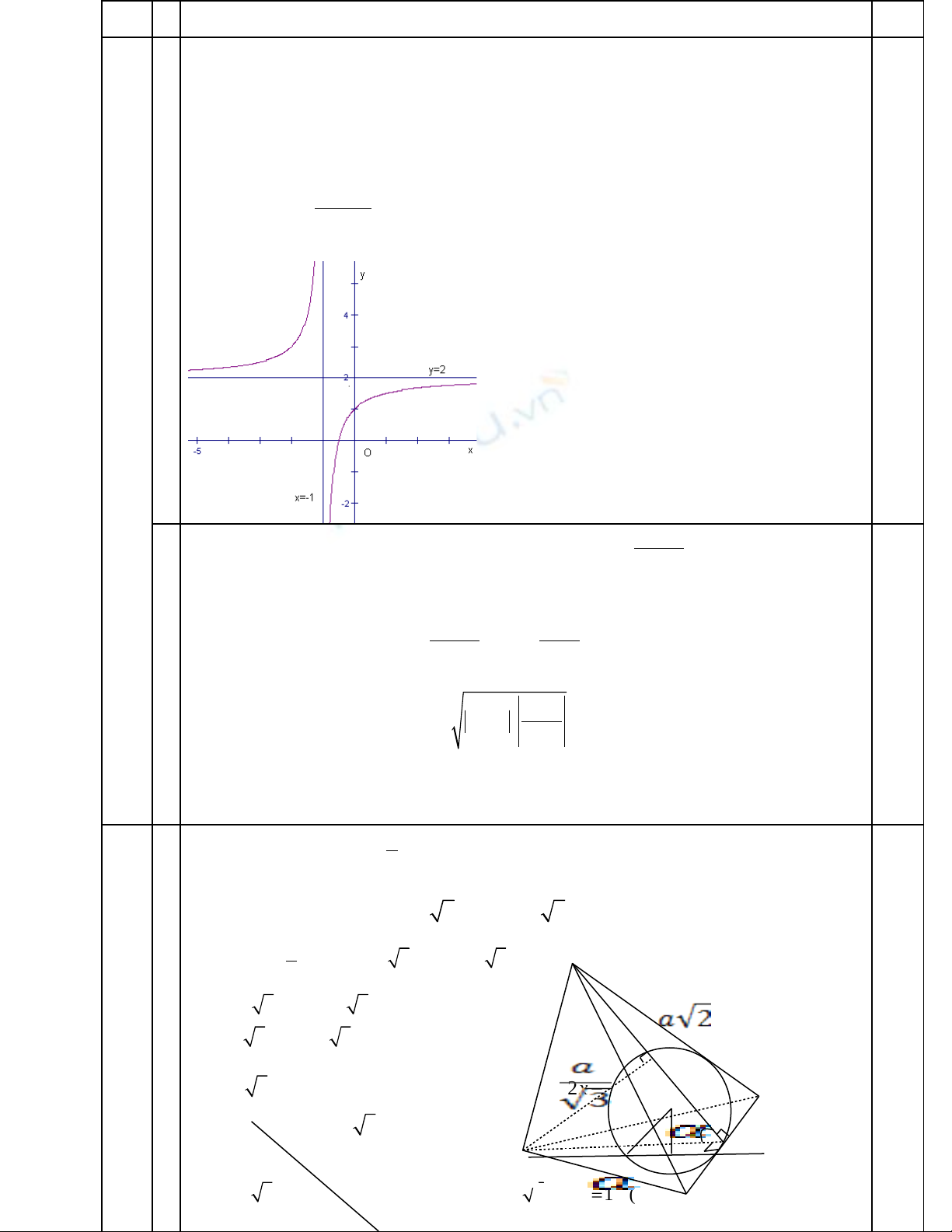
1.Kh o sát s bi n thiên và v đ th (C) c a hàm s đã choả ự ế ẽ ồ ị ủ ố
2.Tìm trên đ th (C) nh ng đi m có t ng kho ng cách đ n hai ti m c n c a (C) nhồ ị ữ ể ổ ả ế ệ ậ ủ ỏ
nh t.ấ
Câu II (2,0 đi m)ể 1. Gi i h ph ng trình: ả ệ ươ
2 2
3 3
2 1
2 2
y x
x y y x
− =
− = −
.
2.Gi i ph ng trình sau:ả ươ
( )
6 6
8 sin cos 3 3 sin 4 3 3 cos 2 9sin 2 11x x x x x
+ + = − +
.
Câu III (1,0 đi m)ể Tính tích phân: I =
1
2
1
2
1
( 1 )
xx
x e dx
x
+
+ −
.
Câu IV(1,0 đi m)ể Cho t di n ABCD có AC = AD = aứ ệ
2
, BC = BD = a, kho ng cách t B đ nả ừ ế
m t ph ng (ACD) b ngặ ẳ ằ
3
a
. Tính góc gi a hai m t ph ng (ACD) và (BCD). Bi t th c a kh iữ ặ ẳ ế ể ủ ố
t di n ABCD b ng ứ ệ ằ
3
15
27
a
.
Câu V (1,0 đi m)ể V i m i s th c ớ ọ ố ự x, y th a đi u ki n ỏ ề ệ
( )
2 2
2 1x y xy+ = +
. Tìm giá tr l n nh t vàị ớ ấ
giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
.
II. PH N RIÊNGẦ (3,0 đi m)ể Thí sinh ch đ c làm m t trong hai ph n (ph n A ho c B)ỉ ượ ộ ầ ầ ặ
A.Theo ch ng trình Chu nươ ẩ
Câu VI.a( 2,0 đi m)ể
1. Trong mp v i h t a đ Oxy cho đ ng tròn : xớ ệ ọ ộ ườ 2 +y2 - 2x +6y -15=0 (C ). Vi t PT đ ng th ng (Δ)ế ườ ẳ
vuông góc v i đ ng th ng: 4x-3y+2 =0 và c t đ ng tròn (C) t i A;B sao cho AB = 6.ớ ườ ẳ ắ ườ ạ
2.Trong không gian v i h t a đ Oxyz cho hai đ ng th ng: dớ ệ ọ ộ ườ ẳ 1 :
2 1
4 6 8
x y z− +
= =
− −
và
d2 :
7 2
6 9 12
x y z− −
= =
−
. Xét v trí t ng đ i c a dị ươ ố ủ 1 và d2 . Cho hai đi m A(1;-1;2) và B(3 ;- 4;-2), Tìmể
t a đ đi m I trên đ ng th ng dọ ộ ể ườ ẳ 1 sao cho IA + IB đ t giá tr nh nh t. ạ ị ỏ ấ
Câu VII.a (1,0 đi m) ểCho
1
z
,
2
z
là các nghi m ph c c a ph ng trình ệ ứ ủ ươ
2
2 4 11 0z z− + =
. Tính giá trị
c a bi u th c A = ủ ể ứ
2 2
1 2
2
1 2
( )
z z
z z
+
+
.
B. Theo ch ng trình Nâng cao.ươ
Câu VI.b(2,0 đi m)ể
1.Trong m t ph ng Oxy cho elip (E): ặ ẳ
2 2
1
4 3
x y
+ =
và đ ng th ng ườ ẳ
∆
:3x + 4y =12. T đi m M b t kìừ ể ấ
trên
∆
k t i (E) các ti p tuy n MA, MB. Ch ng minh r ng đ ng th ng AB luôn đi qua m t đi m cẻ ớ ế ế ứ ằ ườ ẳ ộ ể ố
đ nh.ị
2.Trong không gian v i h t a đ Oxyz , cho M(1;2;3). L p ph ng trình m t ph ng đi qua M c t baớ ệ ọ ộ ậ ươ ặ ẳ ắ
tia Ox t i A, Oy t i B, Oz t i C sao cho th tích t di n OABC nh nh t.ạ ạ ạ ể ứ ệ ỏ ấ
Câu VII.b (1,0 đi m) ểGi i h ph ng trình:ả ệ ươ
+=+
+=+
yyxx
xyyx
222
222
log2log72log
log3loglog
……………H t………………ế
Thí sinh không đ c s d ng tài li u, cán b coi thi không gi i thích gì thêm.ượ ử ụ ệ ộ ả
H và tên thí sinh: ………………………………………… S báo danh: ……………………ọ ố
ĐÁP ÁN Đ THI TH TOÁN (Đ 181)Ề Ử Ề
Câu Ý N i dungộĐiể
m
I
1* TËp x¸c ®Þnh: D = R\{ - 1}
* Sù biÕn thiªn
- Giíi h¹n vµ tiÖm cËn:
lim lim 2
x x
y y
+ −
= =
; tiÖm cËn ngang: y = 2
( 1) ( 1)
lim ; lim
x x
y y
− +
− −
= + = −
; tiÖm cËn ®øng: x = - 1
- B¶ng biÕn thiªn
Ta cã
2
1
' 0
( 1)
yx
= >
+
víi mäi x
- 1
Hµm sè ®ång biÕn trªn mçi kho¶ng (-
∞
; -1) vµ ( -1; +
∞
)
1đ
2Gäi M(x0;y0) lµ mét ®iÓm thuéc (C), (x0
- 1) th×
0
0
0
2 1
1
x
yx
+
=+
Gäi A, B lÇn lît lµ h×nh chiÕu cña M trªn TC§ vµ TCN th×
MA = |x0+1| , MB = | y0- 2| = |
0
0
2 1
1
x
x
+
+
- 2| = |
0
1
1x+
|
Theo Cauchy th× MA + MB
2
0
0
1
x 1 . 1x
++
=2
MA + MB nhá nhÊt b»ng 2 khi x0 = 0 hoÆc x0 = -2.Như vËy ta cã hai ®iÓm
cÇn t×m lµ M(0;1) vµ M’(-2;3)
0,5
0,5
II
1
( )
6 6 2
3
sin 1 sin 2 (1)
4
x cos x x
+ = −
Thay (1) vµo ph¬ng tr×nh (*) ta cã :
( )
6 6
8 sin 3 3 sin 4 3 3 2 9sin 2 11x cos x x cos x x
+ + = − +
2
2
2
3
8 1 sin 2 3 3 sin 4 3 3 2 9sin 2 11
4
3 3 sin 4 3 3 2 6sin 2 9sin 2 3
3 sin 4 3 2 2sin 2 3sin 2 1
x x cos x x
x cos x x x
x cos x x x
� �
− + = − +�� �
� �
− = − +�
− = − +�
( )
( )
( )
3 2 . 2sin 2 1 (2sin 2 1)(sin 2 1)
2sin 2 1 3 2 sin 2 1 0
cos x x x x
x cos x x
− = − −�
− − + =�
2sin 2 1 0 2sin 2 1 (2)
3 2 sin 2 1 0 sin 2 3 2 1 (3)
x x
cos x x x cos x
− = =
� �
� �
� �
− + = − =
� �
Gi¶i (2) :
12 ( )
5
12
x k
k Z
x k
Π
= + Π
Π
= + Π
; Gi¶i (3)
4( )
7
12
x k
k Z
x k
Π
= + Π
Π
= + Π
0,5
0,5
H
D
E
C
B
A
I
A H B
N u thí sinh làm bài không theo cách nêu trong đáp án mà v n đúng thì đ c đ đi m t ng ph n nhế ẫ ượ ủ ể ừ ầ ư
đáp án quy đ nh.ị
------------------H tế------------------