NHÓM TOÁN VD – VDC THI PHC-LN 3
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
TRƯỜNG THPT THÁI PHÚC
.
ĐỀ THI THỬ ĐẠI HỌC LẦN 1 NĂM 2020
Môn: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Đề thi gồm 06 trang - 50 câu trắc nghiệm
_____________________________
Họ và tên: ……………………………………………………… SBD: …………………
Câu 1: Từ các chữ số
1;2;3;4;5
lập được bao nhiêu số tự nhiên có
5
chữ số đôi một khác nhau.
A.
3125.
B.
120.
C.
720.
D.
Câu 2: Cho dãy số
n
u
là cấp số cộng. Biết
35
12, 18uu
. Tìm
7?u
A.
6.
B.
21.
C.
24.
D.
27.
Câu 3: Diện tích xung quanh của một hình nón có bán kính đáy
r
và độ dài đương sinh
l
bằng:
A.
2 ( )rl
. B.
()rl
.
C.
rl
. D.
2)rl
.
Câu 4: Hàm số
32
3xyx
đồng biến trên khoảng nào dưới đây?.
A.
2;0
. B.
;2
.
C.
2; 
. D.
0;2
.
Câu 5: Một khối nón có độ dài đường cao bằng
8
, độ dài đường sinh bằng
10
. Thể tích của khối nón
đó bằng:
A.
288
. B.
96
. C.
360
. D.
120
.
Câu 6: Nghiệm của phương trình
31
327
x
là:
A.
5x
. B.
6x
. C.
5x
. D.
1x
.
Câu 7: Nếu
3
08f x dx
và
5
35f x dx
thì
5
0f x dx
bằng
A.
13
. B.
3
. C.
5
. D.
0
.
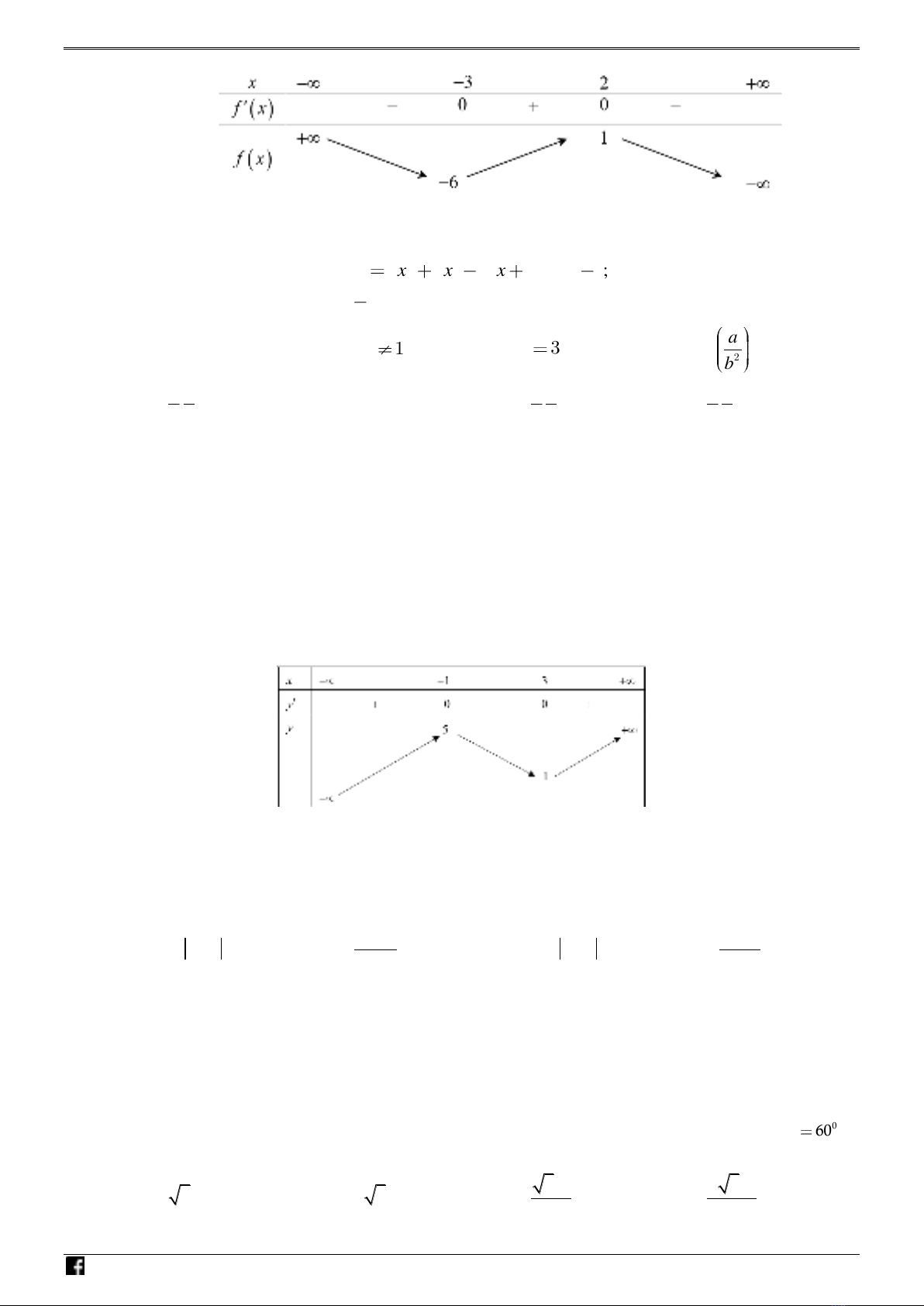
Câu 8: Cho hàm số
y f x
liên tục trên
3;2
và có bảng biến thiên như sau. Gọi
,Mm
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x
trên đoạn
1;2
. Giá trị của
2Mm
bằng:
x
3
1
0
1
2
'fx
0
0
0
0
fx
2
3
0
2
1
A.
7
. B.
8
. C.
6
. D.
3
.
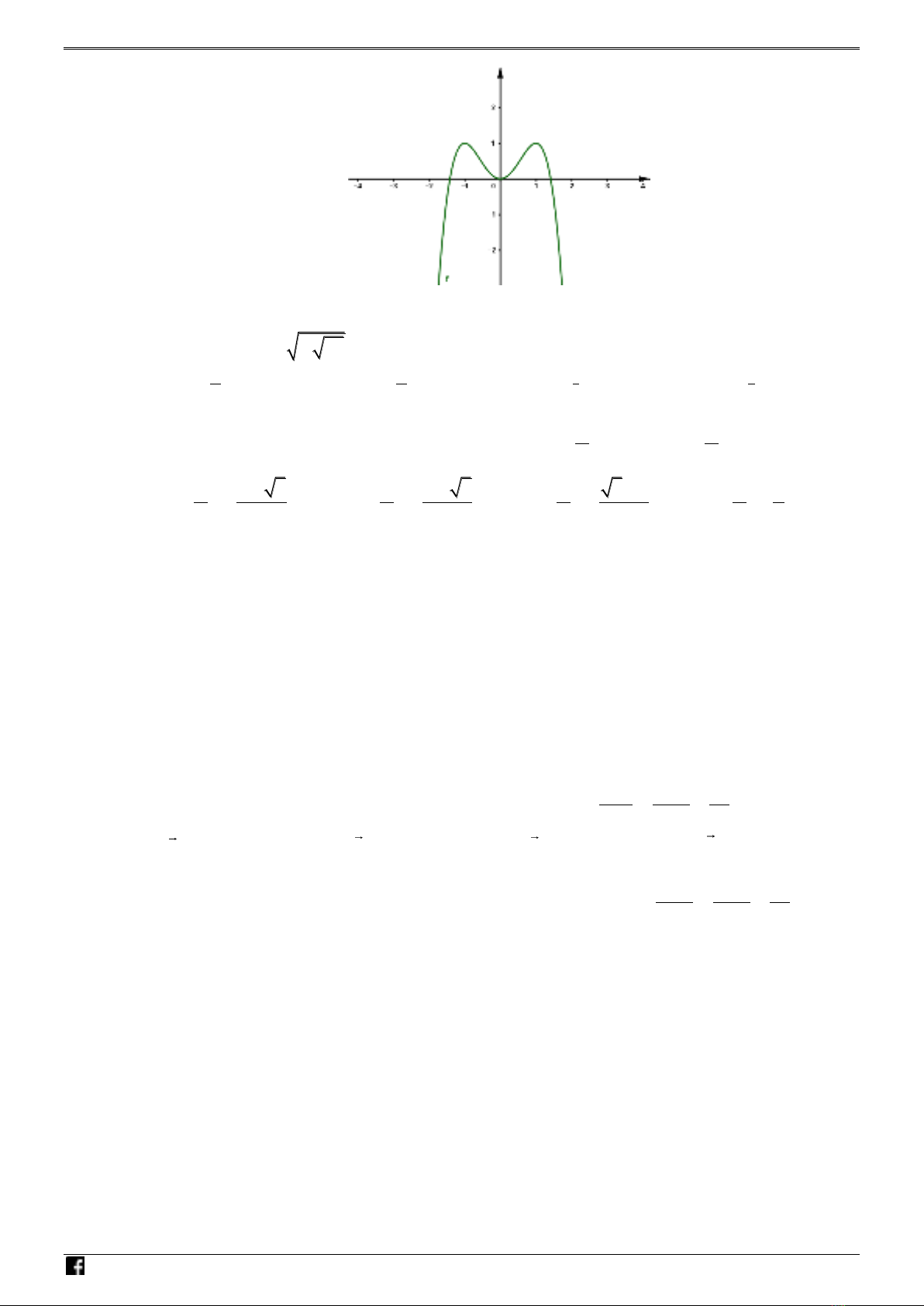
Câu 9: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số nào dưới đây
NHÓM TOÁN VD – VDC THI PHC-LN 3
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
42
2.y x x
B.
42
2.y x x
C.
22.y x x
D.
32
2 1.y x x x
Câu 10: Cho biểu thức
432
. , 0P a a a
. Mệnh đề nào sau đây đúng ?
A.
5
12
Pa
. B.
7
12
Pa
. C.
3
4
Pa
. D.
3
2
Pa
.
Câu 11: Cho
()Fx
la một nguyên hàm của
( ) cos2f x x
vad
1.
4
F



Tính
?
3
F



A.
23
34
F



. B.
23
34
F



. C.
32
34
F



. D.
1
32
F



.
Câu 12: Số phức
35zi
có phần ảo bằng?
A. 5. B.
5i
. C. 3. D.
3
.
Câu 13: Trong không gian
Oxyz
, hình chiếu vuông góc của
5; 4;2M
lên mặt phẳng
Oxy
là đểm
nào?
A.
10; 4;2M
. B.
15;0;2M
. C.
35; 4;0M
. D.
45;4;0M
.
Câu 14: Trong không gian
Oxyz
, mặt cầu
2 2 2
: 4 2 4 10 0S x y z x y z
có tâm là điểm nào?
A.
4;2;4I
. B.
4; 2; 4I
. C.
2; 1; 2I
. D.
2;1;2I
.
Câu 15: Trong không gian
Oxyz
, vectơ chỉ phương của đường thẳng
13
2 1 1
x y z


là
A.
2;1; 1u
. B.
1; 3;0u
. C.
1;3;0u
. D.
2;1;1u
.
Câu 16: Trong không gian
Oxyz
, tọa độ giao điểm
M
của đường thẳng
23
:2 1 1
x y z
d

với mặt
phẳng
Oyz
là
A.
2;4;0M
. B.
2; 4;0M
. C.
0; 4;1M
. D.
2;4;1M
.
Câu 17: Cho khối tứ diện
ABCD
có thể tích bằng
3
60cm
và điểm
K
trên cạnh
AC
sao cho
3AC KC
.
Tính thể tích
V
của khối tứ diện
BKCD
.
A.
3
20V cm
. B.
3
12V cm
. C.
3
30V cm
. D.
3
15V cm
.
Câu 18: Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
NHÓM TOÁN VD – VDC THI PHC-LN 3
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
5; 0
. B.
3; 
. C.
2;1
. D.
2; 3
.
Câu 19: Giá trị nhỏ nhất của hàm số
y x x x
32
2 3 12 2
trên
;12
là
A.
6
. B.
5
. C.
15
. D.
11
.
Câu 20: Cho
,ab
là hai số dương với
a1
thỏa mãn
logab3
. Khi đó, giá trị
logb
a
b2
bằng
A.
5
3
. B.
1
. C.
1
3
. D.
2
3
.
Câu 21: Bất phương trình
2
2 18.2 32 0
xx
có tập nghiệm là:
A.
;1 4;
. B.
;1 16;
. C.
;2 16;
. D.
;2 4;
.
Câu 22: Cho hình trụ có thiết diện qua trục là hình vuông, diện tích mặt đáy bằng
2
16 cm
. Tính diện
tích xung quan của hình trụ đó.
A.
2
27
xq
S cm
. B.
2
32
xq
S cm
. C.
2
64
xq
S cm
. D.
2
16
xq
S cm
.
Câu 23: Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên
Số nghiệm thực của phương trình
3 5 0fx
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 24: Họ nguyên hàm của hàm số
cotf x x
là
A.
ln sin xC
. B.
2
1
sin C
x
. C.
ln sin xC
. D.
2
1
sin C
x

.
Câu 25: Độ giảm huyết áp của một bệnh nhân được đo bởi công thức
2
0,025 30G x x x
trong đó
x mg
và
0x
là liều lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì
cần tiêm cho bệnh nhân một liều lượng bằng:
A.
20mg
. B.
30mg
. C.
40mg
. D.
15mg
.
Câu 26: Cho khối lăng trụ đứng
.ABCD A B C D
có đáy là hình thoi cạnh
a
, góc
0
60ABC
và
4AA a
, thể tích khối lăng trụ đó bằng
A.
3
3a
. B.
3
23a
. C.
3
3
3
a
. D.
3
23
3
a
.
NHÓM TOÁN VD – VDC THI PHC-LN 3
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 27: Tiệm cận đứng của đồ thị hàm số
2
1
32
x
yx
x
là
A.
2x
. B.
1x
. C.
0x
. D.
1x
và
2x
.
Câu 28: Cho hàm số
32
y ax bx cx d
có đồ thị là đường cong trong hình dưới đây. Mệnh đề nào
sau đây đúng?
A.
0, 0, 0a c d
. B.
0, 0, 0a c d
. C.
0, 0, 0a c d
. D.
0, 0, 0a c d
.
Câu 29: Cho hàm số
y f x
liên tục trên đoạn
;ab
. Gọi
D
là hình phẳng giới hạn bởi đồ thị
:C y f x
, trục hoành, hai đường thẳng
,x a x b
(như hình vẽ bên dưới).
Giả sử
D
S
là diện tích của hình phẳng
D
thì:
A.
0
0
b
D
a
S f x dx f x dx

. B.
0
0
b
D
a
S f x dx f x dx

.
C.
0
0
b
D
a
S f x dx f x dx

. D.
0
0
b
D
a
S f x dx f x dx

.
Câu 30: Gọi
12
,zz
là hai nghiệm của phương trình
22z 10 0z
, với
1
z
có phần ảo dương,
2
z
có
phần ảo âm. Số phức
12
2zz
được xác định bằng
A.
33i
. B.
33i
. C.
13i
. D.
13i
.
Câu 31: Trong mặt phẳng với hệ tọa độ
Oxy
điểm
3; 5M
biểu diễn hình học của số phức nào?
A.
35i
. B.
53i
. C.
35i
. D.
53i
.
Câu 32: Trong không gian
Oxyz
, mặt phẳng
P
đi qua
2;1;3M
và song song với mặt phẳng
Q
:
2 3 4 0x y z
có phương trình là
A.
2 3 12 0x y z
. B.
2 3 12 0x y z
.
C.
2 3 14 0x y z
. D.
2 3 13 0x y z
.
NHÓM TOÁN VD – VDC THI PHC-LN 3
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 33: Trong không gian
Oxyz
, mặt cầu tâm
0; 4;0I
và đi qua điểm
0; 3;0M
có phương trình
A.
2
22
35x y z
. B.
2
22
41x y z
.
C.
2
22
3 25x y z
. D.
2
22
4 25x y z
.
Câu 34: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 3 5 0P x y z
. Vectơ nào
KHÔNG PHẢI vectơ pháp tuyến của mặt phẳng
()P
?
A.
1;2; 3n
. B.
1; 2;3n
. C.
1; 2;3n
. D.
2; 4;6n
.
Câu 35: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
1;0;0 , 0;2;0 , 0;0; 3A B C
. Phương
trình nào dưới đây là phương trình của mặt phẳng
ABC
?
A.
1
1 2 3
x y z
. B.
1
1 2 3
x y z
. C.
0
1 2 3
x y z
. D.
1
1 2 3
x y z
.
Câu 36: Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu nhiên
10
học sinh gồm năm nam
và năm nữ vào ngồi hai dãy ghế sao cho mỗi ghế có đúng một người ngồi. Xác suất để mỗi học
sinh nam ngồi đối diện với một học sinh nữ bằng
A.
8
63
. B.
1
1080
. C.
8
55
. D.
.
Câu 37: Cho khối lăng trụ
.ABC A B C
có thể tích bằng
3
12a
và điểm
M
là một điểm nằm trên cạnh
CC
sao cho
3MC MC
. Tính thể tích của khối tứ diện
AB MC
theo
.a
A.
3
2a
. B.
3
4a
. C.
3
3a
. D.
3
a
.
Câu 38: Cho
1
0
d1xf x x

và
1 10f
. Tích phân
1
0
df x x
bằng
A.
8
. B.
11
. C.
10
. D.
9
.
Câu 39: Cho hàm số
9mx
yxm
(m là tham số thực). Có bao nhiêu giá trị nguyên m để hàm số nghịch
biến trên khoảng
(0; )
?
A. 5 B. 4 C. 3 D. Vô số
Câu 40: Cho hình nón có độ dài đường cao bằng
8
, một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo thiết diện là tam giác đều có diện tích bằng
25 3
. Thể tích của khối nón giới hạn bởi
hình nón nói trên bằng:
A.
96 3
. B.
128
. C.
96
. D.
64 3
.
M
C'
B'
A
B
C
A'