Trang 1
TRƯỜNG THPT MINH LONG ĐỀ THAM KHẢO KỲ THI TNTHPT NĂM 2025
TỔ: TOÁN – LÝ TIN MÔN TOÁN
Thời gian làm bài 90 phút
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
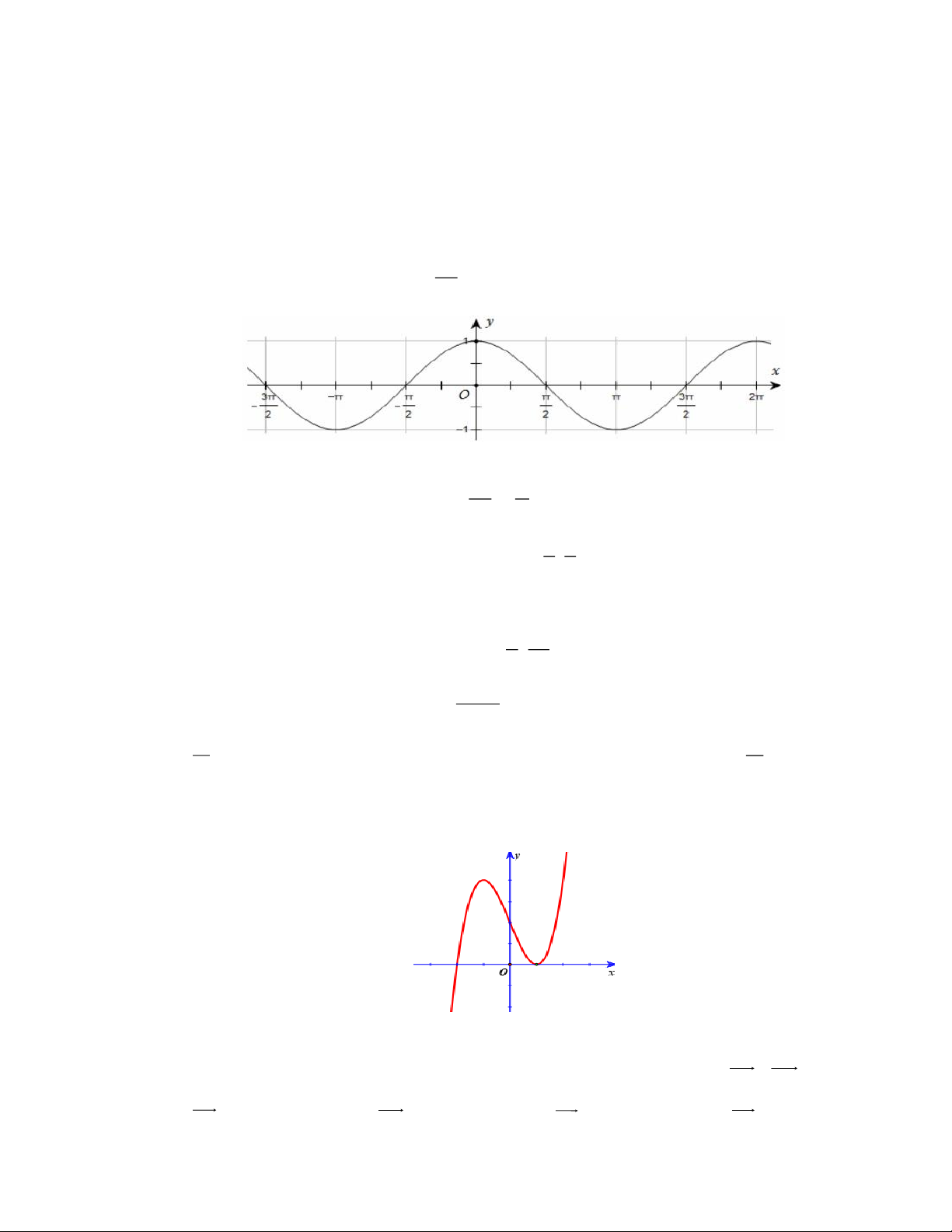
Câu 1: Cho hàm số
cosyx
trên đoạn
3;2
2



có đồ thị như hình vẽ bên
Trong các mệnh đề sau mệnh đề nào đúng?
A. Hàm số đồng biến trên khoảng
3;
22





.
B. Hàm số đã cho nghịch biến trên khoảng
;
22




.
C. Hàm số đã cho đồng biến trên khoảng
0
.
D. Hàm số nghịch biến trên các khoảng
;
22



.
Câu 2: Tìm giá trị nhỏ nhất của hàm số
21
2
x
yx
trên đoạn
3;5
.
A.
. B.
5
. C.
7
. D.
11
3
.
Câu 3: Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm
số nào?
A.
332y x x
. B.
32
1y x x
. C.
221y x x
. D.
332y x x
Câu 4: Trong không gian
Oxyz
, cho 3 điểm
,,A B C
phân biệt. Hiệu hai véc tơ
AB AC
bằng
A.
.CB
B.
BC
. C.
BA
. D.
CA
.
Trang 2
Câu 5 : Trong không gian với hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, một máy bay
dân dụng của Mỹ đang bay với vận tốc và hướng không đổi từ điểm
)400;1( 50;12A
đến điểm
)700;2( 50;15B
trong
phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay, hãy tính
tọa độ của điểm
E
là vị trí của máy bay sau
10
phút tiếp theo kể từ điểm
B
.
A.
850
800; ;15
3
E


B.
850
600; ;15
3
E


C.
650
600; ;15
3
E


D.
650
600; ;14
3
E


Câu 6: Trong không gian
Oxyz
, cho hai điểm
1;2;1M
và
3;1; 2N
. Đường thẳng
MN
có
phương trình là
A.
1 2 1
4 3 1
x y z

. B.
1 2 1
2 1 3
x y z


.
C.
1 2 1
4 3 1
x y z

. D.
1 2 1
2 1 3
x y z


.
Câu 7: Người ta đếm số xe ô tô đi qua một trạm thu phí mỗi phút trong khoảng thời gian từ 9
giờ đến 9 giờ 30 phút sáng. Kết quả được ghi lại ở bảng sau:
Tính số trung bình cộng của mẫu số liệu ghép nhóm trên.
A.
27
. B.
52
3
. C.
28
. D.
53
3
.
Câu 8: Cho mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình và bác An:
Thời gian
15;20
20;25
25;30
35;40
Số ngày tập của bác Bình
5
12
8
2
Số ngày tập của bác
0
25
5
0
Gọi
12
,RR
lần lượt là khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục
buổi
sáng của bác Bình, bác An. Tìm
12
,.RR
A.
12
25, 10.RR
B.
12
10, 25.RR
C.
12
5, 5.RR
D.
12
25, 25.RR
Câu 9: Tìm một nguyên hàm
Fx
của hàm số
32f x x x
, biết
01F
.
A.
32
1F x x x
. B.
32
1F x x x
.
C.
32
F x x x
. D.
32
1F x x x
.
Trang 3
Câu 10: Có bao nhiêu cách chọn một tổ trưởng và một tổ phó từ nhóm học tập gồm 5 học
sinh? A. 20. B. 10. C. 25. D. 7.
Câu 11: Cho hai biến cố
,AB
với
( ) ( )
0,7; 0,3P B P AB==
. Tính
( )
/P A B
A.
3
7
. B.
1
2
C.
6
7
. D.
1
7
.
Câu 12: Viết ba số hạng xen giữa các số 2 và 22 để được một cấp số cộng có năm số hạng. Ba
số hạng đó lần lượt là:
A.
7;12;17
. B.
6;10;14
C.
8;13;18
. D.
6;12;18.
PHẦN II: Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh
chọn đúng hoặc sai.
Câu 1: Cho hàm số
y f x
có bảng biến thiên dưới đây:
Các mệnh đề sau đúng hay sai?
a) Hàm số đạt cực đại tại
1x
.
b) Hàm đồng biến trên
0;
.
c) Giá trị lớn nhất của hàm số trên
1;1
bằng
3.
d) Có 3 giá trị nguyên của tham số
m
để phương trình
2 3 0f x m
có 4 nghiệm
phân biệt.
Câu 2: Trong không gian
Oxyz
, cho đường thẳng
3
12
1 2 3


:y
xz
D
và mặt phẳng
2 3 0 :P x y z
.
a) Số đo góc giữa hai đường thẳng
D
và
P
bằng
a
với
21
sin 7
.
b) Tọa độ giao điểm của đường thẳng
D
và
P
là điểm
1; 4;3H
.
c) Phương trình mặt phẳng
Q
vuông góc với mặt phẳng
P
và chứa đường thẳng
D
là
0x y z
.
Trang 4
d) Đường thẳng
2
d
vuông góc với
P
tạo với
30:Q x my
một góc
30o
. Khi đó
tổng tất cả các giá trị của tham số
m
bằng
16
5
.
Câu 3: Vào năm
2014
, dân số nước ta khoảng
90,7
triệu người. Giả sử, dân số nước ta sau
t
năm được xác định bởi hàm số
St
(đơn vị: triệu người), trong đó tốc độ gia tăng dân số được
cho bởi
0,014
1,2698.e ,
t
St
với
t
là số năm kể từ năm
2014
,
St
tính bằng triệu người/ năm.
a)
St
là một nguyên hàm của
St
.
b)
0,014
90,7.e 90,7.
t
St
c) Theo công thức trên, tốc độ tăng dân số nước ta năm
2034
(làm tròn đến hàng phần mười
của triệu người/ năm) khoảng
1,7
triệu người/ năm.
d) Theo công thức trên, dân số nước ta năm
2034
(làm tròn đến hàng đơn vị của triệu người) là
khoảng
120
triệu người/ năm.
Câu 4. Một tổ chuyên môn Toán – Tin ở trường cấp 3 của tỉnh X có 6 giáo viên Toán gồm có 3
nam và 3 nữ, giáo viên Tin học thì có 3 giáo viên gồm 2 nữ và 1 nam. Các mệnh đề sau đúng
hay sai?
a) Có
3.2 6
cách chọn ra hai giáo viên nữ từ các số giáo viên trong tổ.
b) Có
6.3 18
cách chọn ra hai giáo viên gồm 1 nam, 1 nữ từ số giáo viên trong tổ.
c) Có 63 cách chọn ra một đoàn kiểm tra nội bộ gồm 3 người có đủ 2 môn Toán và Tin
d) Có
9
cách chọn ra 2 giáo viên gồm 1 nam, 1 nữ và có đủ cả 2 môn.
PHẦN III: Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Nếu
là chênh lệch nhiệt độ ban đầu giữa một vật
A
và các vật xung quanh, và nếu
các vật xung quanh có nhiệt độ
S
T
, thì nhiệt độ của vật
A
tại thời điểm
t
(giờ) được mô hình
hóa bởi hàm số:
() 0kt
T t T R e
S
(trong đó
k
là hằng số dương phụ thuộc vào vật
A
).
Một con ngỗng nướng được lấy từ lò nướng khi nhiệt độ của nó đã đạt đến
350 F
và được đặt
trên một bàn trong một căn phòng có nhiệt độ là
90 F
. Sau nửa giờ nhiệt độ của gà tây là
140 F
, hỏi nhiệt độ của nó sau 60 phút là bao nhiêu? (làm tròn kết quả đến phần chục).
Câu 2. Một nhà máy có hai phân xưởng
I
và
II
. Phân xưởng
I
sản xuất
53%
số sản phẩm và
phân xưởng
II
sản xuất
47%
số sản phẩm. Tỉ lệ sản phẩm bị lỗi của phân xưởng
I
là
10%
và
của phân xưởng
II
là
8%
. Kiểm tra ngẫu nhiên một sản phẩm của nhà máy. Xác suất để sản
phẩm đó bị lỗi bằng.
(làm tròn kết quả đến hàng phần trăm).
Trang 5
Câu 3: Cắt một vật thể
V
bởi hai mặt phẳng vuông góc với
Ox
tại
0, .xx

Một mặt
phẳng vuông góc với
Ox
tại
(0 )xx

cắt vật thể (V) theo thiết diện là một tam giác đều có
cạnh
2 sin .x
Tính thể tích vật thể giới hạn bởi hai mặt phẳng nói trên. (Kết quả làm tròn đến
hàng phần trăm).
Câu 4. Một thùng rượu vang có dạng khối tròn xoay với bán kính hai mặt đáy là 33 cm, bán
kính mặt cắt ở chính giữa thùng là 43 cm. Chiều cao của thùng rượu là 112 cm, bao gồm phần
thân thùng rượu, hai đế đỡ thùng rượu (mỗi đế cao 3 cm) và thùng rượu được ghép từ các thanh
gỗ sổi với độ dày mỗi thanh gỗ là 3 cm (Hình minh họa phía dưới).
Biết rằng phần bên ngoài thùng rượu có dạng một khối tròn xoay tạo thành khi quay một phần
của parabol
()P
:
2
y ax bx c
quanh trục hoành. Hỏi thùng rượu đó chứa được tối đa bao
nhiêu lít rượu (làm tròn kết quả đến hàng đơn vị)?
Câu 5. Khi gắn hệ tọa độ
Oxyz
(đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt
phẳng
()Oxy
trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí
(5; 0; 5)A
đến
vị trí
(10; 1 0; 3)B
và hạ cánh tại vị trí
( ; ; 0).M a b
Giá trị của
ab
bằng bao nhiêu (viết kết quả
dưới dạng số thập phân)?
Câu 6. Trong một đợt kiểm tra sức khoẻ, có một loại bệnh X mà tỉ lệ người mắc bệnh là
0,2%
và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính.
Tuy nhiên, có
6%
những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y.
Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương
tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu (làm tròn kết quả đến
hàng phần trăm)?
--------------------Hết------------------
HƯỚNG DẪN GIẢI.
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
Câu
1
2
3
4
5
6
7
8
9
10
Chọn
C
A
D
A
A
B
D
A
A
A
Câu
11
12
Chọn
A
A