ĐỀ THI VÀO LỚP 10 PTNK 2008 - 2009
MÔN TOÁN AB
(chung cho các lớp Toán, Tin, Lý, Hoá, Sinh)
Câu 1. Cho phương trình:
2 2
x mx 2m
2m 1 x 6
x 2m
(1)
a)Giải phương trình (1) khi m = -1.
b)Tìm tất cả các giá trị của m để phương trình (1) có nghiệm.
Câu 2. a) Giải phương trình:
2x – 1– 2 x– 1 1.
b)Giải hệ phương trình: 2
2
2x –x 2y 4xy
x 2xy 4
Câu 3. a) Chứng minh rằng biểu thức sau không phụ thuộc vào biến x ( với x > 1):
A=
x x 4x 3 x x x – 1
b) Cho a, b, c là các số thực khác 0 và thoả mãn điều kiện:
a + 2b – 3c = 0
bc + 2ac – 3ab = 0
Chứng minh rằng: a = b = c.
Câu 4. Cho tứ giác nội tiếp ABCD có góc A nhọn và hai đường chéo AC, BD vuông góc
nhau. Gọi M là giao điểm của AC và BD, P là trung điểm của CD và H là trực tâm của
tam giác ABD.
a) Hãy xác định tỉ số PM:DH.
b) Gọi N và K lần lượt là chân đường cao kẻ từ B và D của tam giác ABD;
Q là giao điểm của hai đường thẳng KM và BC. Chứng minh rằng MN = MQ.
c) Chứng minh rằng tứ giác BQNK nội tiếp được.
Câu 5. Một nhóm học sinh cần chia đều một lượng kẹo thành các phần quà để tặng cho
các em nhỏ ở một đơn vị nuôi trẻ mồ côi. Nếu mỗi phần quà giảm 6 viên kẹo thì các em
sẽ có thêm 5 phần quà nữa, còn nếu mỗi phần quà giảm 10 viên kẹo thì các em sẽ có
thêm 10 phần quà nữa. Hỏi nhóm học sinh trên có bao nhiêu viên kẹo?
Giải
Caâu 1: Vôi m = - 1 thì (1) trôû thaønh: 2
x x 2
3x 6 ÑK:x 2
x 2
x + 1 = - 3x + 6 (vì x2 – x – 2 = (x + 1)(x –
2))
x =
5
4
(thoûa)
b) ÑK: x ≠ - 2m, (1) coù theå vieát:
x m x 2m
2m 1 x 6
x 2m
x – m = (2m –
1)x + 6
2(1 – m)x = 6 + m (2)
(1) coù nghieäm (2) coù nghieäm khaùc – 2m
2
1 m 0 m 1
m 1
6 m
3
x 2m 2m 2m 3 0 m 2hoaëcm
2 1 m
4
Caâu 2: a) Phöông trình coù theå vieát laïi:
2x 1 1 2 x 1 ñk:x 1
. Bình phöông 2
veá , thu goïn ñöôïc:
2x 1 x 2
. Ñieàu kieän x ≥ 2, bình phöông 2 veá phöông trình ñöôïc 2x – 1 = x2 – 4x
+ 4
hay x2 – 6x + 5 = 0 x = 1(loaïi) hoaëc x = 5 (thoûa). Vaäy phöông trình coù 1 nghieäm x =
5.
b) Phaân tích phöông trình 1 thaønh (x – 2y)(2x – 1) = 0 x = 2y hoaëc 2x – 1 = 0.
Giaûi 2 heä 2 2
x 2y 0 2x 1 0
hoaëc
x 2xy 4 x 2xy 4
2 2
x 2
2
1 1
y
x x
x 2y 2
2 2
hoaëc hoaëc
15 15
4y 4y 4 x 2
y y
4 4
2
y2
Vaäy heä ñaõ cho coù 3 nghieäm:
2 2 1 15
2; ; 2; ; ;
2 2 2 4
Caâu 3: a) vôùi x > 1:
3
x x x 3x 3 x x 1 x x 1 x 3 x 1 x x 1
A 1
x 1 x 1 x x x 1 x 3 x 1 x 1 x x x 1 x 3

b) a + 2b – 3c = 0 a – c = 2(c – b) (1)
bc + 2ac – 3ab = 0 bc – ab + 2ac – 2ab = 0 b (c – a) + 2a( c – b) = 0 (2)
(1), (2) b( c – a) + a(a – c) = 0 (c – a)(b – a) = 0 c = a hoaëc a = b.
Neáu c = a thì (1) c = b. Vaäy a = b = c.
Neáu a = b thì (1) 3b – 3 c = 0 b = c. Vaäy a = b = c.
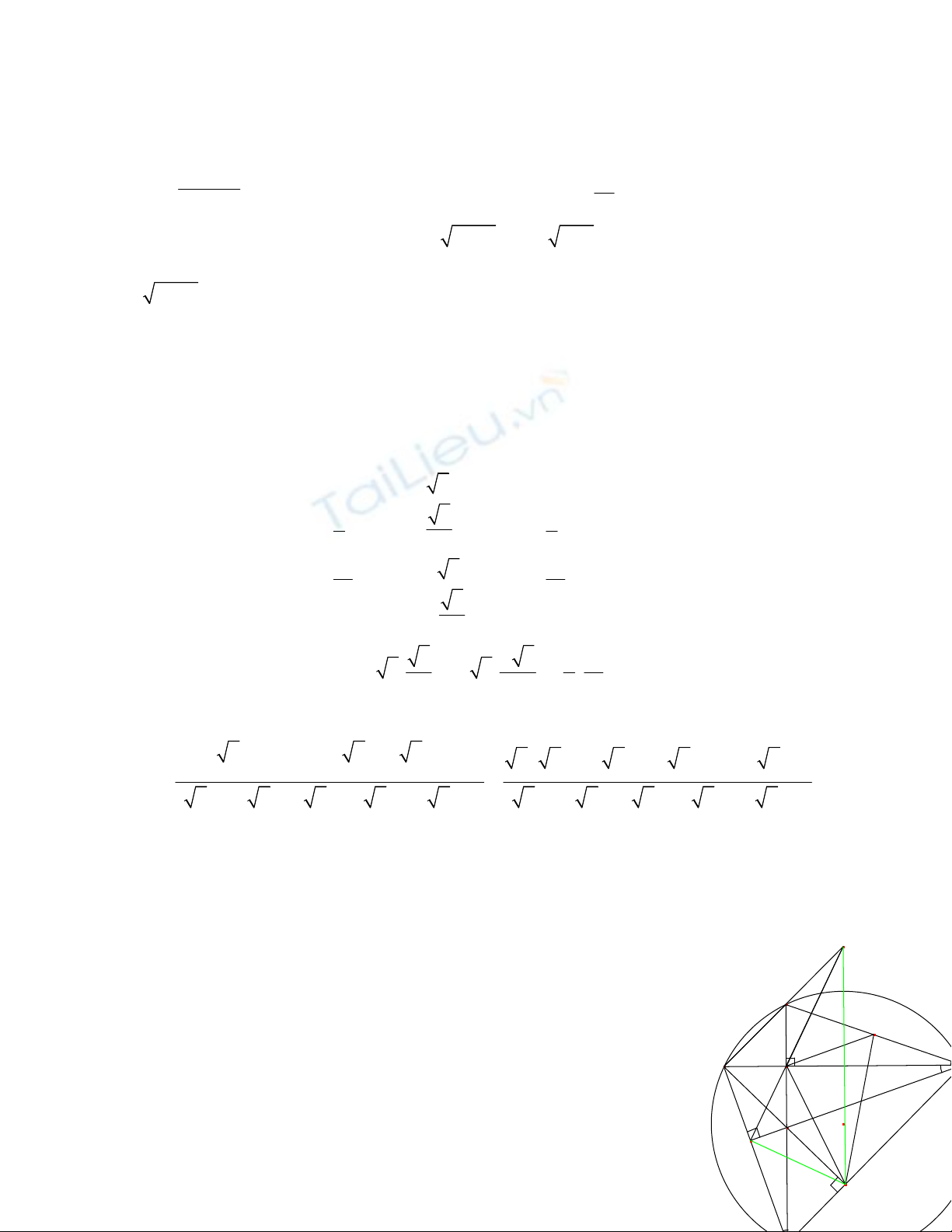
Caâu 4:
a)
·
·
»
·
·
·
·
·
CDB CAB cuøngchaénBC ;BDH CAB cuøngphuï ABD CDB
BDH
CDH coù DM laø ñöôøng cao vöøa laø ñöôøng phaân giaùc neân laø caân
DM cuõng laø trung tuyeán MC = MH, maø PC = PD
MP laø ñöôøng trung bình cuûa CHD PM:DH = ½
C
M
B
/
P
H
K
Q
N
b) ABCD noäi tieáp
· ·
·
QCD BAD cuøngbuøBCD
(1)
AKHN noäi tieáp
·
· ·
BAD NHD cuøngbuøKHN
(2)
DCH caân
·
·
DCM MHD
(3)
(1), (2), (3)
·
·
QCM MHN
(*)
ABMN noäi tieáp
·
·
ABN AMN
; BKHM noäi tieáp
·
·
ABN KMH
·
·
·
KMH HMN CMQ
(**)
MC = MH (***)
(*), (**), (***) MCQ = MHN (g.c.g) MQ = MN.
c) AKHN noäi tieáp
·
·
·
·
·
·
·
BAH KNH,maøBAH BNM KNB BNM BQM
BQNK noäi tieáp.
Caâu 5: Goïi x laø soá vieân keïo cuûa moãi phaàn quaø. ÑK: x > 10, x nguyeân.
y laø soá phaàn quaø maø nhoùm hs coù , y nguyeân döông.
Toång soá vieân keïo cuûa nhoùm laø xy (vieân).
Ta coù heä phöông trình:
x 6 y 5 xy
5x 6y 30 x 30
5x 5y 50 y 20
x 10 y 10 xy
Vaäy nhoùm hoïc sinh coù 30. 20 = 600 vieân keïo.