(§Ò thi nµy cã 01 trang)
Bµi 1. (2,0 ®iÓm) Rót gän c¸c biÓu thøc sau :
a)
2 3 3 27 300
b) 1 1 1
:
1 ( 1)
x x x x x
Bµi 2. (1,5 ®iÓm)
a). Gi¶i ph¬ng tr×nh: x2 + 3x – 4 = 0
b) Gi¶i hÖ ph¬ng tr×nh: 3x – 2y = 4
2x + y = 5
Bµi 3. (1,5 ®iÓm)
Cho hµm sè : y = (2m – 1)x + m + 1 víi m lµ tham sè vµ m
1
2
. H·y x¸c ®Þnh
m trong mçi trêng h¬p sau:
a) §å thÞ hµm sè ®i qua ®iÓm M ( -1;1 )
b) §å thÞ hµm sè c¾t trôc tung, trôc hoµnh lÇn lît t¹i A , B sao cho tam gi¸c
OAB c©n.
Bµi 4.
(2,0 ®iÓm): Gi¶i bµi to¸n sau b»ng c¸ch lËp ph¬ng tr×nh hoÆc hÖ ph¬ng
tr×nh:
Mét ca n« chuyÓn ®éng xu«i dßng tõ bÕn A ®Õn bÕn B sau ®ã chuyÓn ®éng
ngîc dßng tõ B vÒ A hÕt tæng thêi gian lµ 5 giê . BiÕt qu·ng ®êng s«ng tõ A ®Õn
B dµi 60 Km vµ vËn tèc dßng níc lµ 5 Km/h . TÝnh vËn tèc thùc cña ca n« (( VËn
tèc cña ca n« khi níc ®øng yªn )
Bµi 5. (3,0 ®iÓm)
Cho ®iÓm M n»m ngoµi ®êng trßn (O;R). Tõ M kÎ hai tiÕp tuyÕn MA , MB
®Õn ®êng trßn (O;R) ( A; B lµ hai tiÕp ®iÓm).
a) Chøng minh MAOB lµ tø gi¸c néi tiÕp.
b) TÝnh diÖn tÝch tam gi¸c AMB nÕu cho OM = 5cm vµ R = 3 cm.
c) KÎ tia Mx n»m trong gãc AMO c¾t ®êng trßn (O;R) t¹i hai ®iÓm C vµ D
( C n»m gi÷a M vµ D ). Gäi E lµ giao ®iÓm cña AB vµ OM. Chøng minh
r»ng EA lµ tia ph©n gi¸c cña gãc CED.
---------------------- HÕt ----------------------
(C¸n bé coi thi kh«ng gi¶i thÝch g× thªm)
Hä vµ tªn thÝ sinh: ……………………. Sè b¸o danh: ………………...
§¸p ¸n
Bµi 1:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NINH
-------------
KỲ THI TUYỂN SINH LỚP 10 THPT
NĂM HỌC 2009 - 2010
a) A =
3
b) B = 1 +
x
Bµi 2 :
a) x1 = 1 ; x2 = -4
b) 3x – 2y = 4
2x + y = 5
<=> 3x – 2y = 4 7x = 14 x = 2
<=> <=>
4x + 2y = 5 2x + y = 5 y = 1
Bµi 3 :
a) V× ®å thÞ hµm sè ®i qua ®iÓm M(-1;1) => Täa ®é ®iÓm M ph¶i tháa m·n hµm
sè :
y = (2m – 1)x + m + 1 (1)
Thay x = -1 ; y = 1 vµo (1) ta cã: 1 = -(2m -1 ) + m + 1
<=> 1 = 1 – 2m + m + 1
<=> 1 = 2 – m
<=> m = 1
VËy víi m = 1 Th× §T HS : y = (2m – 1)x + m + 1 ®i qua ®iÓm M ( -1; 1)
c) §THS c¾t trôc tung t¹i A => x = 0 ; y = m+1 => A ( 0 ; m+1) => OA =
1
m
c¾t truc hoµnh t¹i B => y = 0 ; x =
1
m
m
=> B (
1
m
m
; 0 ) => OB =
1
2 1
m
m
Tam gi¸c OAB c©n => OA = OB
<=>
1
m
=
1
2 1
m
m
Gi¶i PT ta cã : m = 0 ; m = -1
Bµi 4: Gäi vËn tèc thùc cña ca n« lµ x ( km/h) ( x>5)
VËn tèc xu«i dßng cña ca n« lµ x + 5 (km/h)
VËn tèc ngîc dßng cña ca n« lµ x - 5 (km/h)
Thêi gian ca n« ®i xu«i dßng lµ :
60
5
x
( giê)
Thêi gian ca n« ®i xu«i dßng lµ :
60
5
x
( giê)
Theo bµi ra ta cã PT:
60
5
x
+
60
5
x
= 5
<=> 60(x-5) +60(x+5) = 5(x2 – 25)
<=> 5 x2 – 120 x – 125 = 0
x1 = -1 ( kh«ng TM§K)
x2 = 25 ( TM§K)
VËy v©n tèc thùc cña ca n« lµ 25 km/h.
Bµi 5:
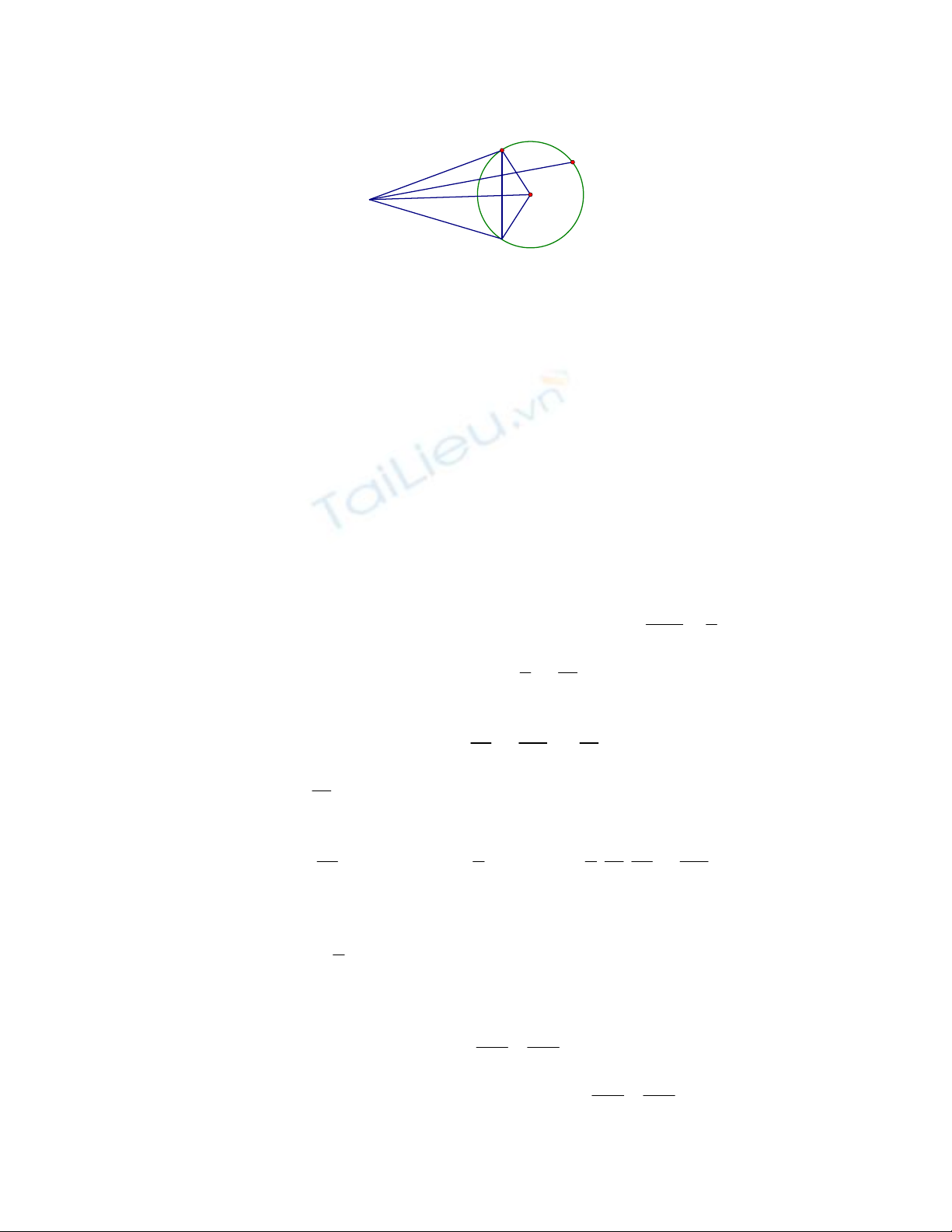
D
CEO
M
A
B
a) Ta cã: MA
AO ; MB
BO ( T/C tiÕp tuyÕn c¾t nhau)
=>
· ·
0
90
MAO MBO
Tø gi¸c MAOB cã :
· ·
MAO MBO
900 + 900 = 1800 => Tø gi¸c MAOB
néi tiÕp ®êng trßn
b) ¸p dông §L Pi ta go vµo
MAO vu«ng t¹i A cã: MO2 = MA2 + AO2
MA2 = MO2 – AO2
MA2 = 52 – 32 = 16 => MA = 4 ( cm)
V× MA;MB lµ 2 tiÕp tuyÕn c¾t nhau => MA = MB =>
MAB c©n t¹i A
MO lµ ph©n gi¸c ( T/C tiÕp tuyÕn) = > MO lµ ®êng trung trùc =>
MO
AB
XÐt
AMO vu«ng t¹i A cã MO
AB ta cã:
AO2 = MO . EO ( HTL trong
vu«ng) => EO =
2
AO
MO
=
9
5
(cm)
=> ME = 5 -
9
5
=
16
5
(cm)
¸p dông §L Pi ta go vµo tam gi¸c AEO vu«ng t¹i E ta cã:AO2 = AE2 +EO2
AE2 = AO2 – EO2 = 9 -
81
25
=
144
25
=
12
5
AE =
12
5
( cm) => AB = 2AE (v× AE = BE do MO lµ ®êng trung
trùc cña AB)
AB =
24
5
(cm) => SMAB =
1
2
ME . AB =
1 16 24
. .
2 5 5
=
192
25
(cm2)
c) XÐt
AMO vu«ng t¹i A cã MO
AB. ¸p dông hÖ thøc lîng vµo tam gi¸c
vu«ng AMO ta cã: MA2 = ME. MO (1)
mµ :
·
·
ADC MAC
=
1
2
S®
»
AC
( gãc néi tiÕp vµ gãc t¹o bëi tiÕp tuyÕn vµ d©y
cung cïng ch¾n 1 cung)
MAC
:
DAM (g.g) =>
MA MD
MC MA
=> MA2 = MC . MD (2)
Tõ (1) vµ (2) => MC . MD = ME. MO =>
MD ME
MO MC
MCE
:
MDO ( c.g.c) (M chung;
MD ME
MO MC
) =>
·
·
MEC MDO
( 2 gãc
tøng) ( 3)
T¬ng tù:
OAE
:
OMA (g.g) =>
OA
OE
=
OM
OA
=>
OA
OE
=
OM
OA
=
OD OM
OE OD
( OD = OA = R)
Ta cã:
DOE
:
MOD ( c.g.c) (
µ
O
chong ;
OD OM
OE OD
) =>
·
·
OED ODM
( 2 gãc
t øng) (4)
Tõ (3) (4) =>
·
·
OED MEC
. mµ :
·
·
AEC MEC
=900
· ·
AED OED
=900
=>
·
·
AEC AED
=> EA lµ ph©n gi¸c cña
·
DEC