
Tiết 43 § 3 . THỰ TỰ TRONG TẬP
HỢP CÁC SỐ NGUYÊN
Số nào lớn hơn : - 10 hay + 1 ?
I.- Mục tiêu :
- Học xong bài này học sinh cần phải :
- Biết so sánh hai số nguyên .
- Tìm được giá trị tuyệt đối của một số nguyên
II.- Phương tiện dạy học :
- Sách Giáo khoa , Hình vẽ trục số
III Hoạt động trên lớp :
1./ On định : Lớp trưởng báo cáo sĩ số lớp
2 ./ Kiểm tra bài cũ:
- Viết tập hợp Z các số nguyên .
- Thế nào là hai số đối nhau ? Tìm số đối
của 12 và - 25
- Kiểm tra bài tập về nhà – Học sinh sữa sai
3./ Bài mới :
Giáo viên Học sinh Bài ghi
- GV nhắc lại so
sánh hai số tự
nhiên.
Ví dụ : 5
> 3
Trên tr
ục số
điểm 3 nằm bên
trái điểm 5 .
- Học sinh so
sánh -5 và –4 ; -
- Học sinh làm
bài tập ?1
I .- So sánh hai số
nguyên :
- Khi biểu diển trên
trục số (nằm ngang)
, điểm a nằm bên
trái điểm b thì số
nguyên a nhỏ hơn
số nguyên b .
Ví dụ :
-5 -4 -3 -
2
-
1 0 1 2 3

2 và –1
-
1 và 0 ;
-5 và 1
4
-5 < -4 -2 <
-1 -1 < 0 -5 <
1
GV hỏi :
- Liền sau số –
2 là số nào
- Tìm số liền
trư
ớc các số
1 , 0 , -1
- So sánh 2 , 5
, 17 ,
1001
với 0 và có
- Học sinh làm
bài tập ?2
2 < 7
-2 > -7
-
4 < 2
-6 < 0
4 > -
2
0 < 3
Chú ý :
Số nguyên b gọi là số
liền sau của số
nguyên a nếu a < b và
không có số nguyên
nào nằm giữa a và b
(lớn hơn a và nhỏ hơn
b) . Khi đó , ta cũng
nói a là số liền trước
của b . Chẳng hạn –5
là số liền trước của –4

kết luận gì ?
- So sánh -1 ,
-3 , -2002 với
0 và có kết
luận gì ?
- So sánh các
số nguyên âm
và các số
nguyên dương
- So sánh
khoảng cách từ
điểm –3 đến
điểm 0 và từ
- Học sinh
nhận xét
- Làm bài tập
?3
- Làm bài tập
?4
.
Nhận xét :
- Mọi số nguyên
dương đều lớn hơn
số 0 .
- Mọi số nguyên âm
đều nhỏ hơn số 0 .
- Mọi số nguyên âm
đều nhỏ hơn bất kỳ
số nguyên dương
nào .
II.- Giá trị tuyệt đối
của một số nguyên :
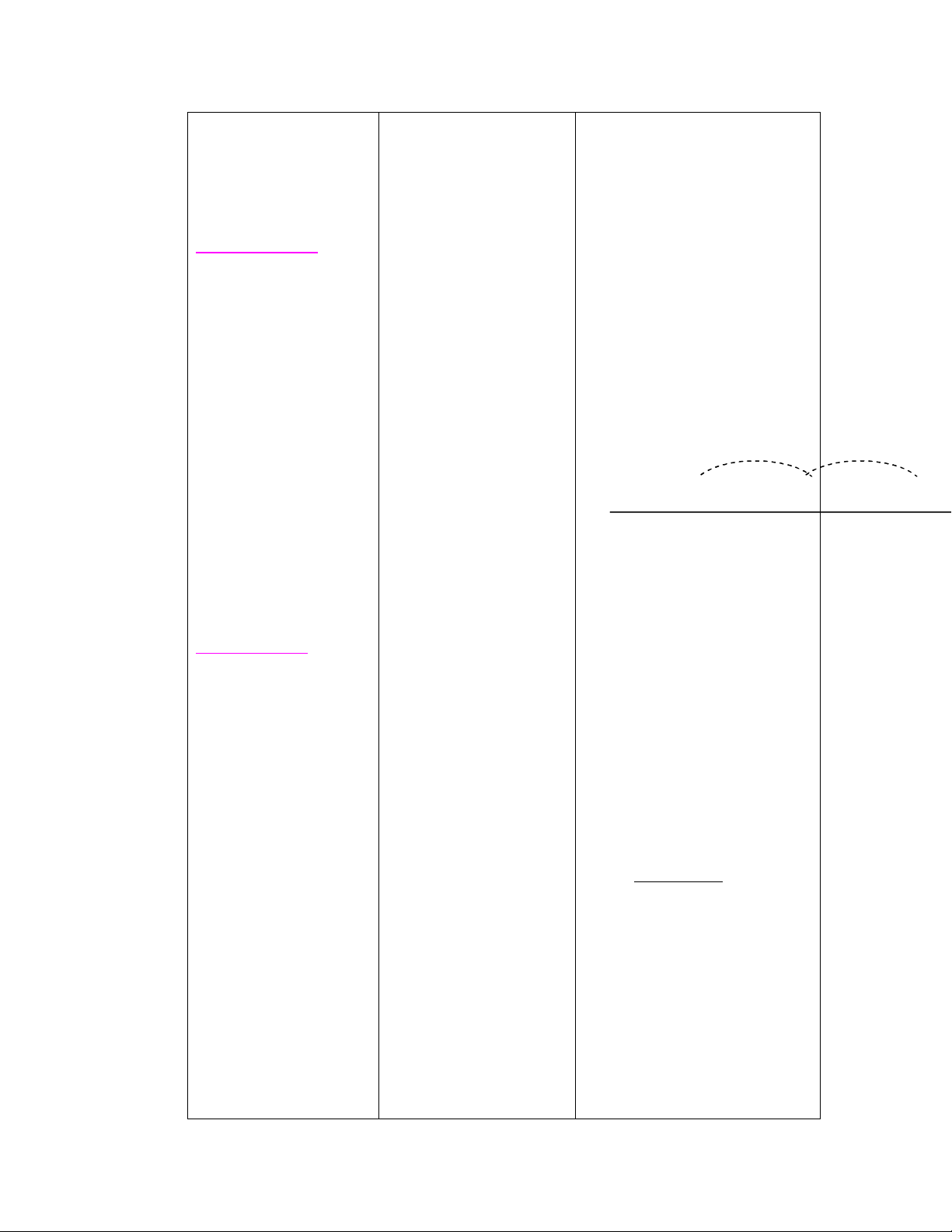
Khoảng cách từ một
điểm a đến điểm 0
trên trục số là giá trị
tuyệt đối của số
điểm 0 đến điểm
3 ?
4./ Củng cố :
Củng cố từng
phần trong từng
bài tập ?
Bài tập 11 và
12 SGK
5./ Dặn dò :
Bài tập về nhà
13 ; 14 ; 15
SGK
nguyên a . Ký hiệu : |
a|
3
đơn vị 3 đơn
vị
-5 -4 -3 -
2
-
1 0 1 2
3 4
| -3 | = 3 ; | 3
| = 3 | -3| = |
3|
* Nhận xét :
- Giá trị tuyệt đối
của số 0 là số 0
- Giá trị tuyệt đối
của một số nguyên


























