Giao thoa ánh sáng nhiều thành phần. Nguyễn văn Đạt, Lạng Giang 1, Bắc Giang
- 1 -
TÍNH SỐ VÂN TỐI KHI THỰC HIỆN
GIAO THOA ÁNH SÁNG NHIỀU THÀNH PHẦN.
Phần này, tôi viết tiếp cho bài giao thoa ánh sáng nhiều thành phần đơn sắc đã upload lên thư viện vật
lý. Nếu bạn nào chưa đọc thì hãy tìm và đọc phần đầu của bài viết trên thư viện, sau đó đọc tiếp phần này
thì có thể sẽ dễ hiểu hơn.
Bài toán giao thoa với ánh sáng nhiều thành phần đơn sắc là một bài toán khó. Việc tính số vân tối
lại càng khó hơn. Có thể có nhiều cách để tính số vân tối đối với bài toán này. Sau đây tôi xin trình bày
cách tính của tôi. Rất mong nhận được góp ý của các thày cô và các bạn học sinh.
Gọi AB là khoảng cách gần nhất giữa hai vân sáng gần nhau nhất ( gọi là khoảng vân trùng). Khi đó:
AB = m.i1
AB = n.i2
Với i1, i2 là khoảng vân khi dùng riêng các bức xạ 1, 2.
Ta xét các khả năng sau:
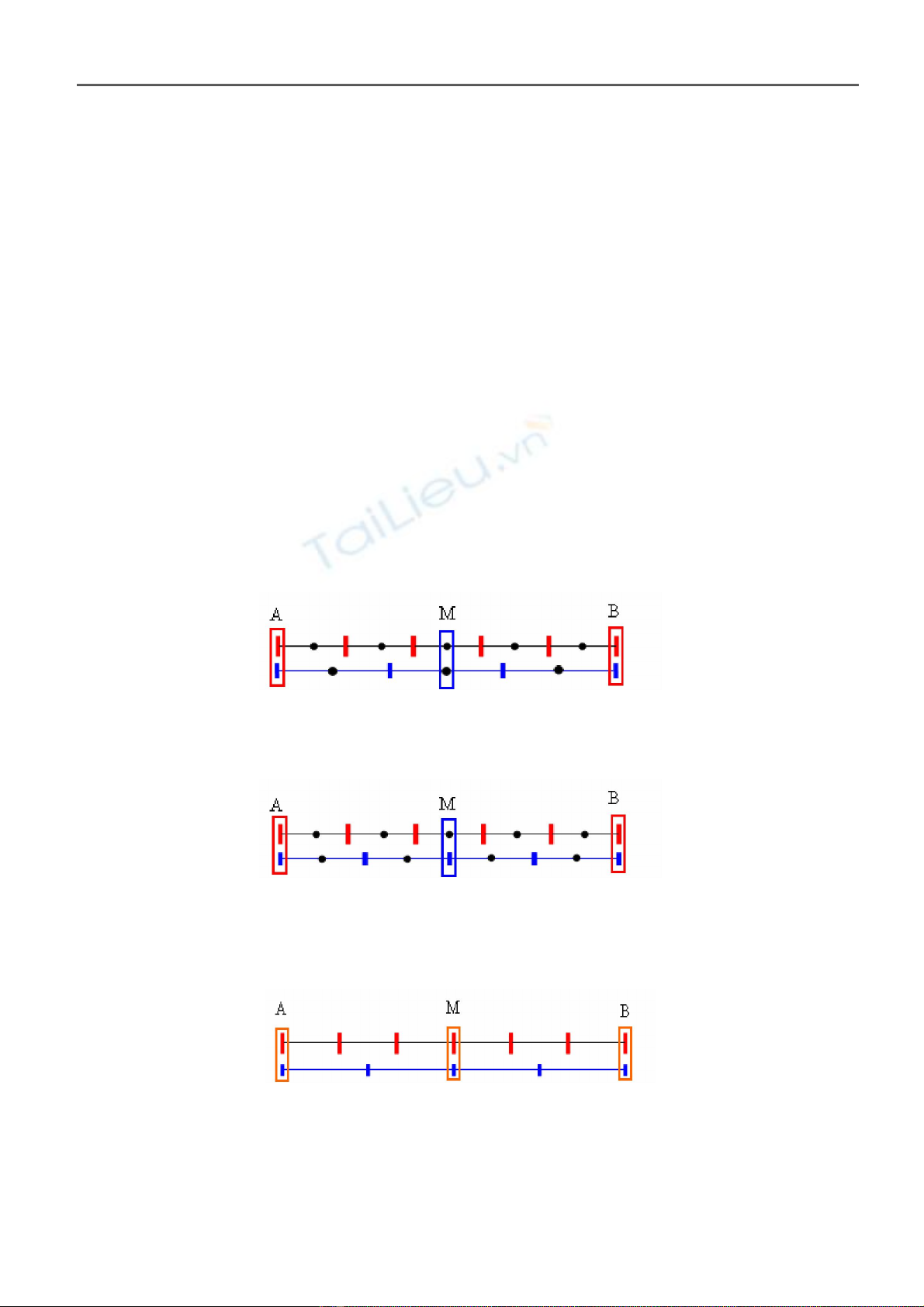
1. cả hai số m, n đều là số lẻ:
(H1)
Khi đó, tại trung điểm M của AB, vân tối của hai bức xạ trùng nhau, tạo thành một vân tối trùng.
2. trong hai số m và n, có một số chẵn, một số lẻ.
(H2)
Khi đó, tại trung điểm M của AB, vân tối của bức xạ này trùng với vân sáng của bức xạ kia, tạo thành
vân sáng đơn sắc (của bức xạ cho vân sáng tại đó)
3. Cả hai số m, n đều chẵn.
(H3)
Khả năng này không thể xảy ra, vì khi đó, tại M là trung điểm của AB, hai vân sáng của hai bức xạ trùng
nhau. AB là khoảng vân trùng thì trong đoạn AB không thể có vân trùng nào khác.
Vậy chỉ có thể có hai khả năng 1 và 2 xảy ra.
Giao thoa ánh sáng nhiều thành phần. Nguyễn văn Đạt, Lạng Giang 1, Bắc Giang
- 2 -
Bây giờ, tôi tạm gọi những điểm có tính chất giống như điểm M ở trường hợp 1 (tại đó hai vân tối trùng
nhau) và ở trường hợp 2 ( tại đó, vân sáng của bức xạ này trùng với vân tối của bức xạ kia) là điểm trùng.
Ta có thể chỉ ra, trên đoạn AB, không còn có điểm trùng nào khác nữa.
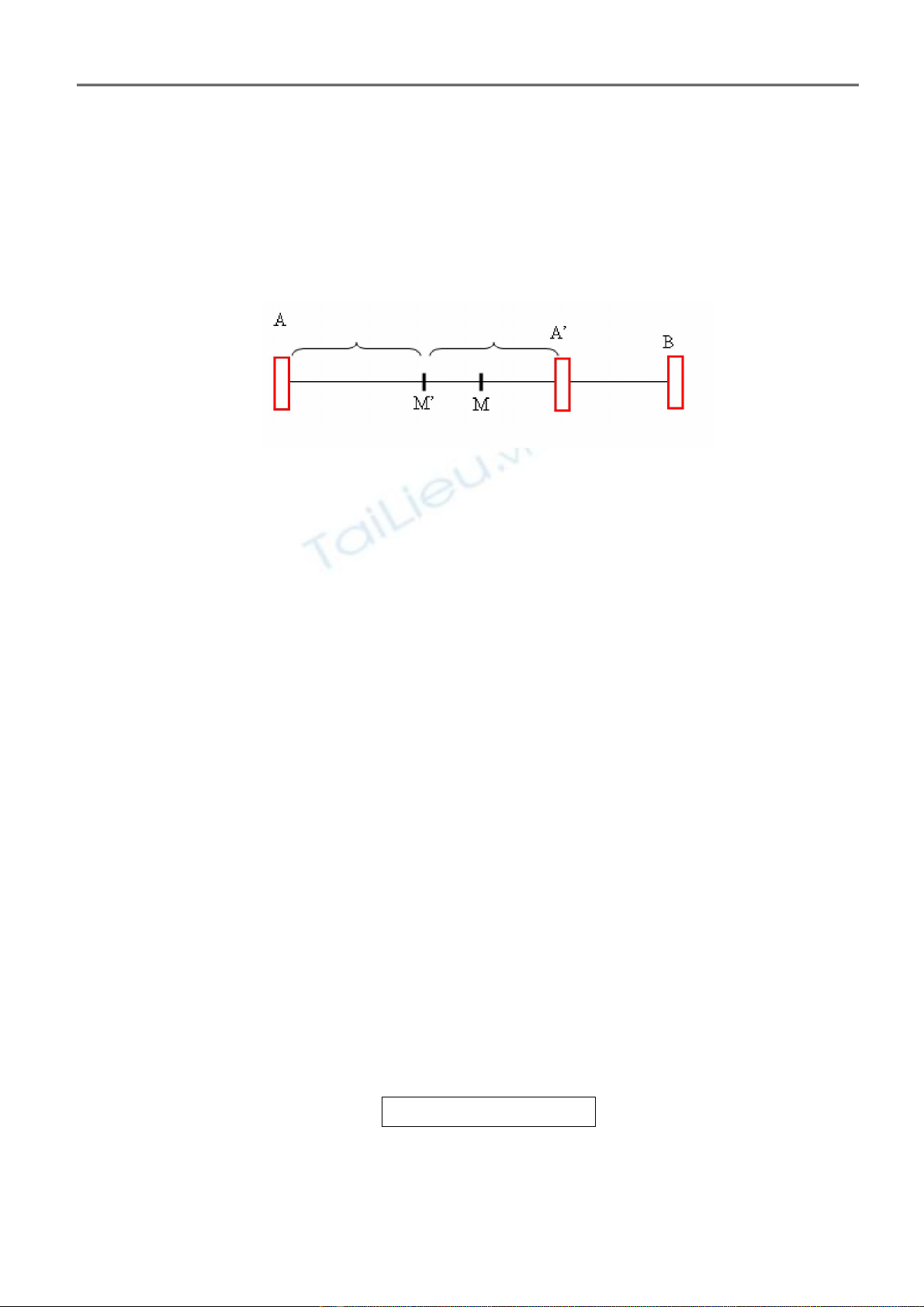
Thật vậy, giả sử trong đoạn AB, có một điểm trùng M’ khác M. Do tính đối xứng, nên điểm A’ đối xứng
với A qua M’ cũng là một vân sáng trùng. ( Bạn đọc hãy dừng ở đây và suy nghĩ tại sao lại vậy)
Vậy khi đó, khoảng vân trùng là AA’ chứ không phải là AB. Điều này là vô lý
Vậy, Trong mỗi khoảng vân trùng, chỉ có duy nhất một điểm trùng, điểm này nằm ở chính giữa khoảng
vân trùng.
Nếu m, n là hai số lẻ thì điểm trùng là một vân tối trùng nhau của hai bức xạ. Trong trường hợp này, ta
dễ dàng suy ra, khoảng cách giữa hai vân tối trùng liên tiếp đúng bằng độ dài của một khoảng vân trùng.
Nếu m, n là hai số một lẻ, một chẵn thì điểm trùng là một vân sáng đơn sắc của một trong hai bức xạ.
Vậy trong trường hợp này, trên toàn bộ trường giao thoa, sẽ không xuất hiện một vân tối trùng nào cả.
Bây giờ, chúng ta hãy suy nghĩ xem, khi điểm trùng xuất hiện, số lượng vân tối của trường giao thoa bị
ảnh hưởng thế nào?
+ Nếu hai vân tối trùng nhau tạo thành một vân tối trùng (H1) thì số vân tối giảm 1.
+ Nếu vân sáng của bức xạ này trùng với vân tối của bức xạ kia để tạo thành điểm trùng (H2) thì số vân
tối cũng giảm 1 ( vì bây giờ, ở vị trí đó là một vân sáng đơn sắc)
Vậy khi một điểm trùng xuất hiện, số vân tối của hệ vân giao thoa sẽ giảm đi 1.
Từ đó ta có thể suy ra cách tính tổng số vân tối trên đoạn MN của trường giao thoa như sau:
+ Tính số vân tối N1 của bức xạ 1.
+ Tính số vân tối N2 của bức xạ 2.
+ Tính số điểm trùng N trùng.
Số vân tối trên đoạn thẳng cần tìm là:
N = N1 + N2 – N trùng.
Giao thoa ánh sáng nhiều thành phần. Nguyễn văn Đạt, Lạng Giang 1, Bắc Giang
- 3 -
Một số ví dụ.
Bài 1.
Thực hiện giao thoa ánh sáng với khe Young. Khoảng cách giữa hai khe sáng F1, F2 là a = 1,2mm,
khoảng cách từ hai khe đến màn quan sát là 1,2m. Ánh sáng được dùng trong thí nghiệm gồm hai bức xạ có
bước sóng 1 = 0,45µm và 2 = 0,6µm. Hỏi trên đoạn OM = 3,5cm có bao nhiêu vị trí mà tại đó hai vân tối
ứng với hai bức xạ trên trùng nhau?
Giải:
Ta có 1 1
2 1 trùng
2 2
i λ 3
3i 4i i
i λ 4
Đây là trường hợp m chẵn, n lẻ.
Tại điểm trùng là vân sáng của bức xạ 1. Trên toàn bộ trường giao thoa không có vân tối trùng.
Bài 2.
Thực hiện giao thoa ánh sáng với khe Young. Khoảng cách giữa hai khe sáng F1, F2 là a = 1,2mm,
khoảng cách từ hai khe đến màn quan sát là 1,2m. Ánh sáng được dùng trong thí nghiệm gồm hai bức xạ có
bước sóng 1 = 0,45µm và 2 = 0,65µm. Hỏi trên đoạn OM = 28,1mm có bao nhiêu vị trí mà tại đó hai vân
tối ứng với hai bức xạ trên trùng nhau?
Giải.
Ta có:
i1 = 0,45mm
i2 = 0,65mm
1trùng
2
i 0, 45 9
i 9.0,65 5,85mm
i 0,65 13
( Có: 13i1 = 9i2. Đây là trường hợp m và n đều lẻ, nên điểm trùng là một vân tối trùng)
trùng
OM 28,1
n 4,8
i 5,85
Số vân tối trùng trên đoạn OM là 5.
Bài 3.
Trong thí nghiệm giao thoa ánh sáng với khe Young, ánh sáng dùng thí nghiệm chứa hai bức xạ 1 =
0,55µm , 2 = 0,65µm. M và N là hai điểm trên màn quan sát và ở hai phía của vân trung tâm. Tại M là vân
sáng bậc 28 của bức xạ 1, tại N là vân sáng bậc 28 của bức xạ 2. Hỏi trên đoạn MN có bao nhiêu vân tối?
Giải.
Ta có: 1 1
2 2
i λ
0,55 11
i
λ 0,65 13
Suy ra itrùng = 13i1 = 11i2
Đây là trường hợp m, n cùng lẻ. Điểm trùng là vị trí trùng nhau của hai vân tối (gọi là vân tối trùng)
Ta có: 1
trùng 1
28iOM
2,15
i 13i
. Trên đoạn OM có hai vân tối trùng.
2
trùng 2
28iON
2,54
i 11i
. Trên đoạn OM có 3 vân tối trùng.
Vậy trên đoạn MN có 5 vân tối trùng.
Giao thoa ánh sáng nhiều thành phần. Nguyễn văn Đạt, Lạng Giang 1, Bắc Giang
- 4 -
Bài 4.
Hãy tính tổng số vân tối trên đoạn MN trong bài tập số 3.
Giải:
Trên đoạn OM;
1
1 1
28iOM
i i
. Có 28 vân tối của bức xạ 1.
1 1
2 2 2
28i iOM 11
28 28. 23,69
i i i 13
. Có 24 vân tối của bức xạ 2.
1
trùng 1
28iOM
2,15
i 13i
. Có 2 vân tối trùng.
Trên đoạn ON
2 2
1 1 1
28i iON 13
28 28. 33,1
i i i 11
. Có 33 vân tối của bức xạ 1.
2
2 2
28iON
28
i i
Có 28 vân tối của bức xạ 2.
2
trùng 2
28iON
2,54
i 11i
. Có 3 vân tối trùng.
Trên cả đoạn MN:
Tổng số vân tối của bức xạ 1 là : 28 + 33 = 61
Tổng số vân tối của bức xạ 2 là : 24 + 28 = 52
Tổng số điểm trùng (vân tối trùng) là 2 + 3 = 5.
Vậy số vân tối trên đoạn MN là N = 61 +52 – 5 =108