
ÑOÀ HOÏA MAÙY TÍNH
Döông Anh Ñöùc, Leâ Ñình Duy Caùc pheùp bieán ñoåi trong ñoà hoïa 2 chieàu 1/16
C
Ca
aùùc
c
p
ph
he
eùùp
p
b
bi
ie
eáán
n
ñ
ño
oååi
i
t
tr
ro
on
ng
g
ñ
ño
oàà
h
ho
oïïa
a
h
ha
ai
i
c
ch
hi
ie
eààu
u
D
Da
aããn
n
n
nh
ha
aääp
p
• Baûn chaát cuûa pheùp bieán ñoåi hình hoïc laø thay ñoåi caùc
moâ taû veà toïa ñoä cuûa ñoái töôïng, töø ñoù laøm ñoái töôïng
thay ñoåi veà höôùng, kích thöôùc, hình daïng.
• Coù hai quan ñieåm veà pheùp bieán ñoåi hình hoïc, ñoù laø:
♦ Bieán ñoåi ñoái töôïng : thay ñoåi toïa ñoä cuûa caùc ñieåm moâ taû
ñoái töôïng theo moät qui taéc naøo ñoù.
♦ Bieán ñoåi heä toïa ñoä : taïo ra moät heä toïa ñoä môùi vaø taát caû
caùc ñieåm moâ taû ñoái töôïng seõ ñöôïc chuyeån veà heä toïa ñoä
môùi.
• Caùc pheùp bieán ñoåi hình hoïc cô sôû : tònh tieán, quay,
bieán ñoåi tæ leä.
C
Ca
aùùc
c
p
ph
he
eùùp
p
b
bi
ie
eáán
n
ñ
ño
oååi
i
h
hì
ìn
nh
h
h
ho
oïïc
c
c
cô
ô
s
sô
ôûû
• Moät pheùp bieán ñoåi ñieåm laø moät aùnh xaï T :
( ) ( )
',',
:22
yxQyxP
RRT
a
→
• Hay T laø haøm soá
(
)
y
x
T
,
theo hai bieán
(
)
y
x
,
:
(
)
( )
=
=
yxgy
y
x
f
x
,'
,
'
ÑOÀ HOÏA MAÙY TÍNH
Döông Anh Ñöùc, Leâ Ñình Duy Caùc pheùp bieán ñoåi trong ñoà hoïa 2 chieàu 2/16
• Pheùp bieán ñoåi affine laø pheùp bieán ñoåi vôùi
(
)
y
x
f
,
vaø
(
)
y
x
g
,
laø caùc haøm tuyeán tính. Pheùp bieán ñoåi naøy coù
daïng :
0,,,,,,,
'
'
≠−∈
++=
++= bcadRfedcba
fdybxy
e
cy
ax
x
• Ta chæ khaûo saùt caùc pheùp bieán ñoåi affine, neân seõ
duøng cuïm töø “pheùp bieán ñoåi” thay cho “pheùp bieán ñoåi
affine”
P
Ph
he
eùùp
p
t
tò
òn
nh
h
t
ti
ie
eáán
n
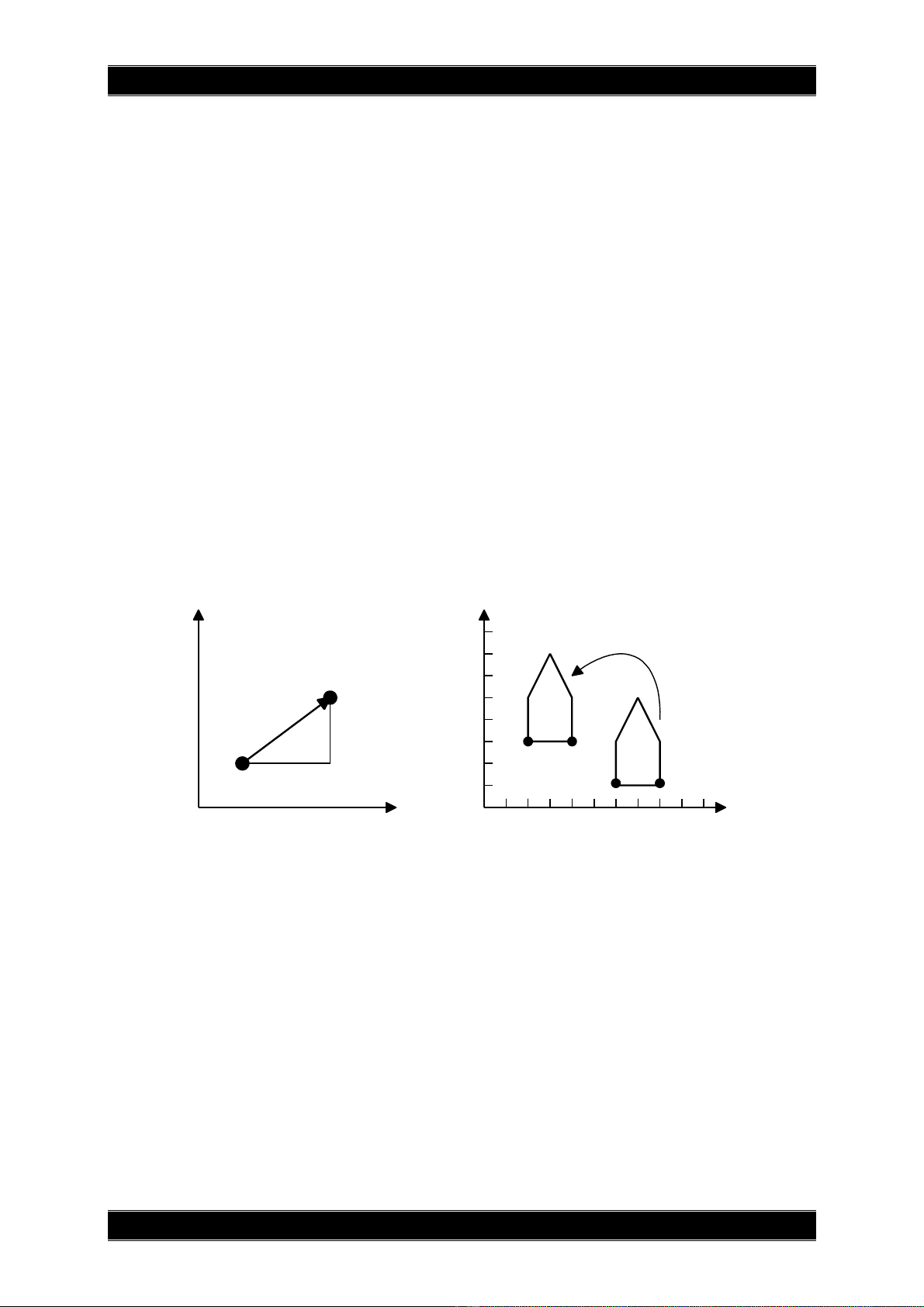
• Pheùp tònh tieán duøng ñeå dòch chuyeån ñoái töôïng töø vò
trí naøy sang vò trí khaùc.
• Neáu goïi x
tr
vaø y
tr
laàn löôït laø ñoä dôøi theo truïc hoaønh
vaø truïc tung thì toïa ñoä cuûa ñieåm môùi
(
)
'
,
'
y
x
Q
sau khi
tònh tieán ñieåm
(
)
y
x
P
,
seõ laø :
+=
+=
y
x
tryy
tr
x
x
'
'
,
(
)
yx
tr
tr
,
ñöôïc goïi laø vector tònh tieán hay vector ñoä dôøi.
P
x
y
Q
tr
x
tr
y
(a)
y
x
(2,3) (4,3)
(6,1) (8,1)
(b)

ÑOÀ HOÏA MAÙY TÍNH
Döông Anh Ñöùc, Leâ Ñình Duy Caùc pheùp bieán ñoåi trong ñoà hoïa 2 chieàu 3/16
P
Ph
he
eùùp
p
b
bi
ie
eáán
n
ñ
ño
oååi
i
t
tæ
æ
l
le
eää
• Pheùp bieán ñoåi tæ leä laøm thay ñoåi kích thöôùc ñoái
töôïng. Ñeå co hay giaõn toïa ñoä cuûa moät ñieåm
(
)
y
x
P
,
theo truïc hoaønh vaø truïc tung laàn löôït laø x
s
vaø y
s
, ta
nhaân x
s
vaø y
s
laàn löôït cho caùc toïa ñoä cuûa P.
=
=
ysy
x
s
x
y
x
.'
.
'
, x
s
vaø y
s
ñöôïc goïi laø caùc heä soá tæ leä.
• Khi caùc giaù trò x
s
, y
s
nhoû hôn 1, pheùp bieán ñoåi seõ
thu nhoû ñoái töôïng, ngöôïc laïi khi caùc giaù trò naøy lôùn
hôn 1, pheùp bieán ñoåi seõ phoùng lôùn ñoái töôïng.
• Khi x
s
, y
s
baèng nhau, ta goïi ñoù laø pheùp ñoàng daïng
(uniform scaling), pheùp ñoàng daïng laø pheùp bieán ñoåi
baûo toaøn tính caân xöùng cuûa ñoái töôïng.
• Taâm tæ leä laø ñieåm khoâng bò thay ñoåi qua pheùp bieán
ñoåi tæ leä.
• Nhaän xeùt raèng khi pheùp bieán ñoåi tæ leä thu nhoû ñoái
töôïng, ñoái töôïng seõ ñöôïc dôøi veà gaàn goác toïa ñoä hôn,
töông töï khi phoùng lôùn ñoái töôïng, ñoái töôïng seõ ñöôïc
dòch chuyeån xa goác toïa ñoä hôn.
y
x
(2,3) (4,3)
(10,1.5)(5,1.5)
ÑOÀ HOÏA MAÙY TÍNH
Döông Anh Ñöùc, Leâ Ñình Duy Caùc pheùp bieán ñoåi trong ñoà hoïa 2 chieàu 4/16
P
Ph
he
eùùp
p
q
qu
ua
ay
y
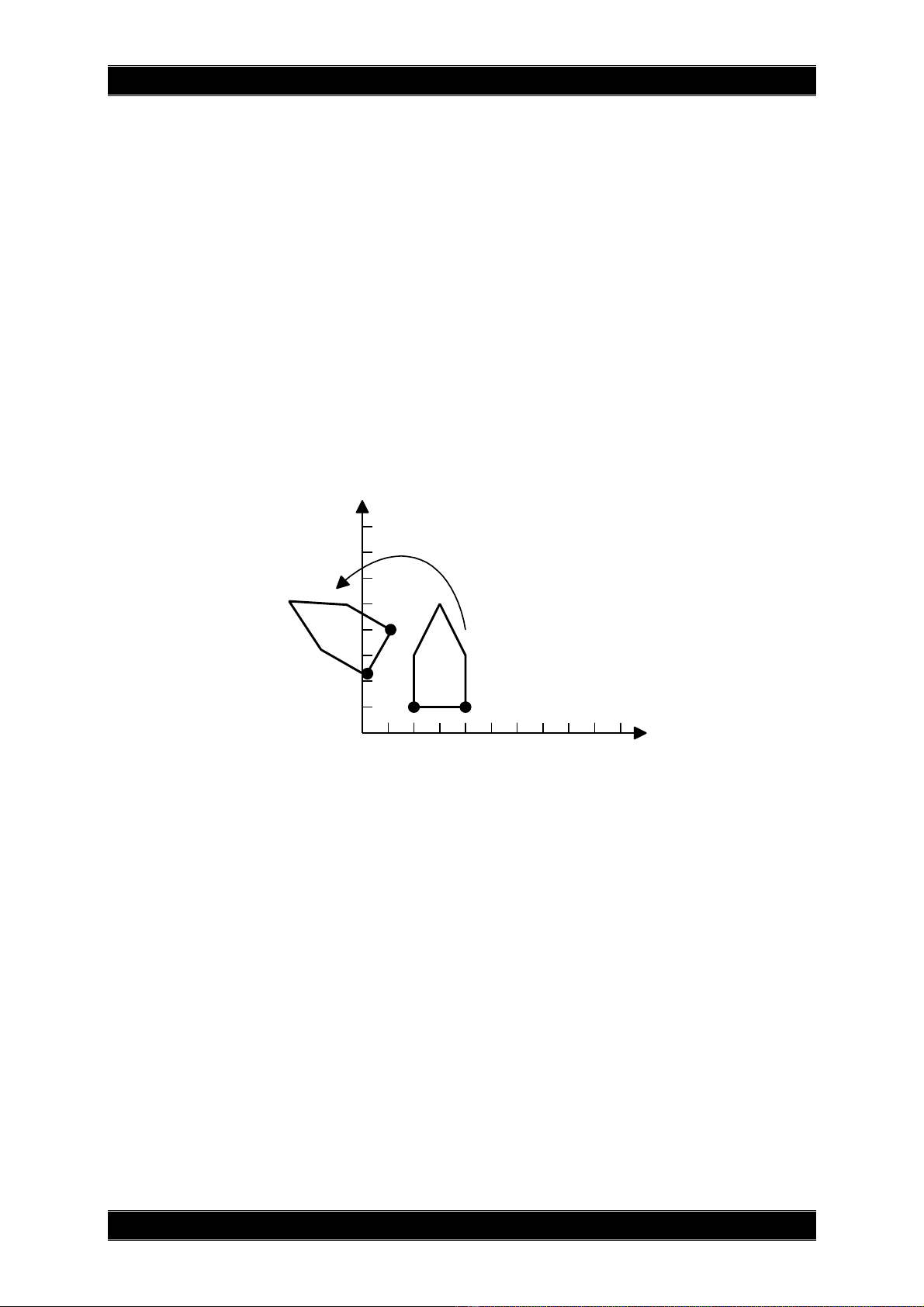
• Pheùp quay laøm thay ñoåi höôùng cuûa ñoái töôïng.
• Moät pheùp quay ñoøi hoûi phaûi coù taâm quay, goùc quay.
Goùc quay döông thöôøng ñöôïc quy öôùc laø chieàu ngöôïc
chieàu kim ñoàng hoà. Ta coù coâng thöùc bieán ñoåi cuûa
pheùp quay ñieåm
(
)
y
x
P
,
quanh goác toïa ñoä moät goùc
α
:
+=
−=
yxy
y
x
x
.cos.sin'
.
sin
.
cos
'
αα
αα
y
x

ÑOÀ HOÏA MAÙY TÍNH
Döông Anh Ñöùc, Leâ Ñình Duy Caùc pheùp bieán ñoåi trong ñoà hoïa 2 chieàu 5/16
H
He
eää
t
to
oïïa
a
ñ
ño
oää
t
th
hu
ua
aààn
n
n
nh
ha
aáát
t
• Toïa ñoä thuaàn nhaát cuûa moät ñieåm treân maët phaúng
ñöôïc bieåu dieãn baèng boä ba soá tæ leä
(
)
h
y
x
hh
,
,
khoâng
ñoàng thôøi baèng 0 vaø lieân heä vôùi caùc toïa ñoä
(
)
y
x
,
cuûa
ñieåm ñoù bôûi coâng thöùc :
h
y
y
h
x
xhh == ,
• Neáu moät ñieåm coù toïa ñoä thuaàn nhaát laø
(
)
z
y
x
,
,
thì noù
cuõng coù toïa ñoä thuaàn nhaát laø
(
)
z
h
y
h
x
h
.
,
.
,
.
trong ñoù h
laø soá thöïc khaùc 0 baát kì.
• Moãi ñieåm
(
)
y
x
P
,
seõ ñöôïc bieåu dieãn döôùi daïng toïa ñoä
thuaàn nhaát laø
(
)
1
,
,
y
x
.


























