90
PhÇn thø hai
TruyÒn nhiÖt
TruyÒn nhiÖt lµ mén khoa häc nghiªn cøu c¸c quy luËt ph©n bè nhiÖt ®é vµ
trao ®æi nhiÖt trong kh«ng gian vµ theo thêi gian gi÷a c¸c vËt cã nhiÖt ®é kh¸c
nhau. Nã lµ phÇn lÝ thuyÕt c¬ së ®Ó tÝnh to¸n c¸c qu¸ tr×nh vµ c¸c thiÕt bÞ trao
®æi nhiÖt trong tù nhiªn vµ kÜ thuËt.
TruyÒn nhiÖt nghiªn cøu c¸c kh¸i niÖm, ®Þnh luËt c¬ b¶n cña c¸c ph−¬ng
thøc trao ®æi nhiÖt vµ øng dông nã ®Ó kh¶o s¸t c¸c qu¸ tr×nh trao ®æi nhiÖt phøc
hîp trong c¸c nhiÖt bÞ n¨ng l−îng nhiÖt.
.
Ch−¬ng 8. c¸c kh¸i niÖm c¬ b¶n
8.1 m« t¶ qu¸ tr×nh trao ®æi nhiÖt
8.1.1 §èi t−îng vµ ph−¬ng ph¸p nghiªn cøu truyÒn nhiÖt
§Ó nghiªn cøu truyÒn nhiÖt, ng−êi ta th−êng dïng hai ph−¬ng ph¸p chñ
yÕu: ph−¬ng ph¸p giai tÝch vµ ph−¬ng ph¸p thùc nghiÖm. Ph−¬ng ph¸p gi¶i tÝch
dùa vµo c¸c ®Þnh luËt c¬ b¶n cña vËt lÝ häc, sö dông c¸c phÐp tÝnh gi¶i tÝch ®Ó dÉn
ra luËt ph©n bè nhiÖt ®é vµ c«ng thøc tÝnh nhiÖt. Ph−¬ng ph¸p thùc nghiÖm dùa
trªn lÝ thuyÕt ®ång d¹ng hoÆc ph©n tÝch thø nguyªn, lËp m« h×nh thÝ nghiÖm ®o
gi¸ trÞ c¸c th«ng sè, xö lÝ sè liÖu ®Ó ®−a ra c«ng thøc thùc nghiÖm.
8.1.2 TÝnh chÊt chung cña hiÖn t−îng trao ®æi nhiÖt
NhiÖt l−îng lµ l−îng n¨ng l−îng trao ®æi gi÷a c¸c phÇn tö thuéc hai vËt cã
nhiÖt ®é kh¸c nhau, tøc cã ®éng n¨ng trung b×nh ph©n tö kh¸c nhau. HiÖn t−îng
trao ®æi nhiÖt chØ xÈy ra gi÷a hai ®iÓm cã nhiÖt ®é kh¸c nhau, tøc cã ®é chªnh
nhiÖt ®é ∆t kh¸c kh«ng> Gi÷a hai vËt c©n b»ng nhiÖt, cã ∆t = 0, nhiÖt l−îng trao
®æi lu«n b»ng kh«ng.
Trong t− nhiªn, nhiÖt l−îng chØ truyÒn theo h−íng tõ ®iÓm cã nhiÖt ®é cao
®Õn ®iÓm cã nhiÖt ®é thÊp. Do ®ã, trao ®æi nhiÖt lµ mét qu¸ tr×nh kh«ng thuËn
nghÞch.
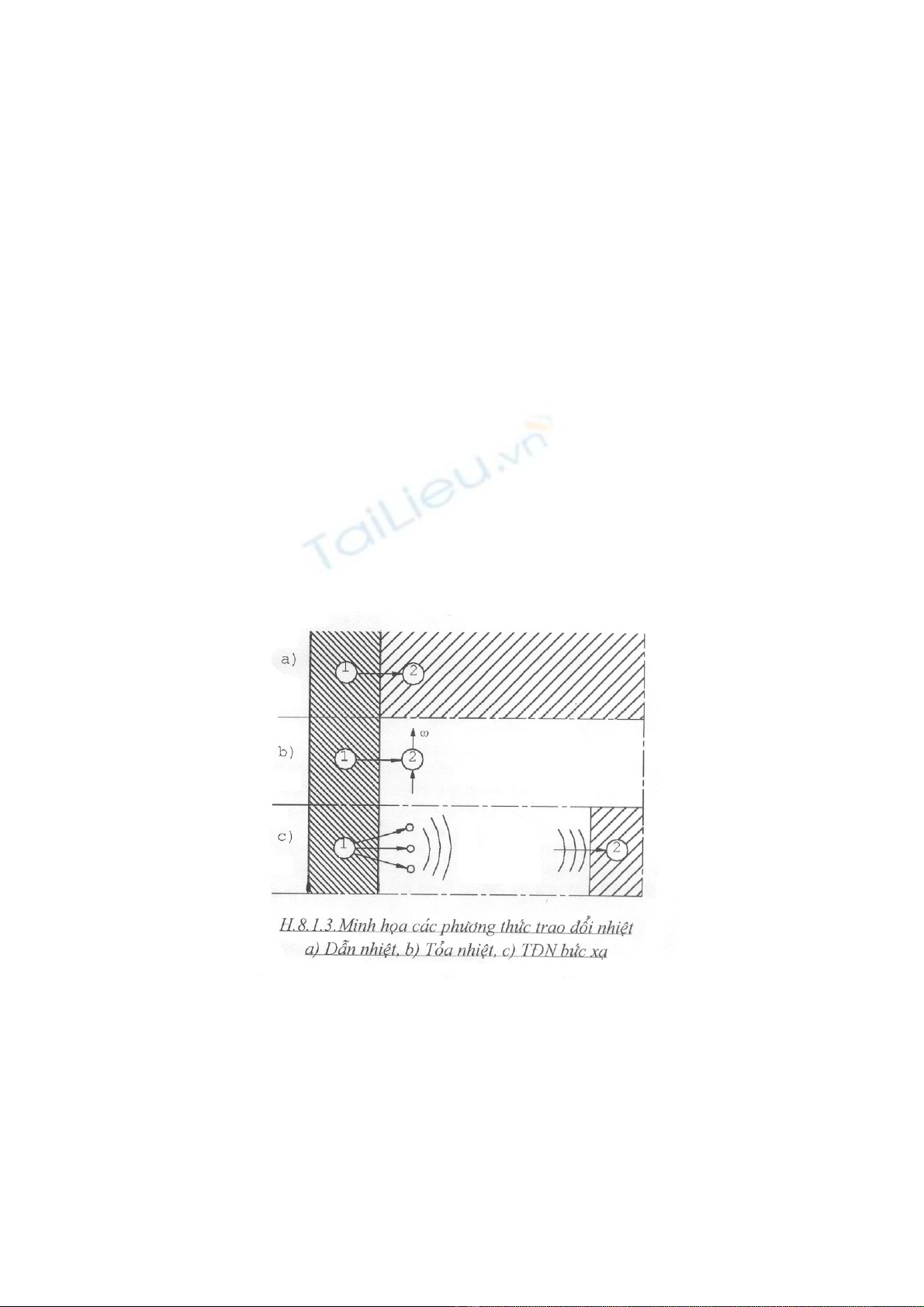
8.1.3. C¸c ph−¬ng thøc trao ®æi nhiÖt
Qu¸ tr×nh trao ®æi nhiÖt cã thÓ ®−îc thùc hiÖn b»ng ba ph−¬ng thøc c¬ b¶n
sau ®©y, ®−îc ph©n biÖt theo ph−¬ng thøc truyÒn ®éng n¨ng gi÷a c¸c ph©n tö
thuéc hai vËt .
8.1.3.1. DÉn nhiÖt
91
DÉn nhiÖt lµ hiÖn t−îng c¸c ph©n tö vËt 1 va ch¹m (trùc tiÕp hoÆc th«ng
qua c¸c ®iÖn tö do trong vËt) vµo c¸c ph©n tö vËt 2 ®Ó truyÒn mét phÇn ®éng
n¨ng. DÉn nhiÖt xÈy ra khi cã sù chªnh lÖch nhiÖt ®é gi÷a c¸c phÇn cña mét vËt
hoÆc gi÷a hai vËt tiÕp xóc nhau. DÉn nhiÖt thuÇn tóy xÈy ra trong hÖ gåm c¸c vËt
r¾n cã sù tiÕp xóc trùc tiÕp.
8.1.3.2. Táa nhiÖt (hay trao ®æi nhiÖt ®èi l−u)
Táa nhiÖt lµ hiÖn t−îng c¸c ph©n tö trªn bÒ mÆt vËt r¾n vµ ch¹m vµo c¸c
phÇn tö chuyÓn ®éng cã h−íng cña mét chÊt láng tiÕp xóc víi nã ®Ó trao ®æi ®éng
n¨ng. Táa nhiÖt xÈy ra t¹i vïng chÊt láng hoÆc khÝ tiÕp xóc víi mÆt vËt r¾n, lµ sù
kÕt hîp gi÷a dÉn nhiÖt vµ ®èi l−u trong líp chÊt láng gÇn bÒ mÆt tiÕp xóc. ChuyÓn
®éng cã h−íng (®èi l−u) cña chÊt láng cã thÓ ®−îc sinh ra mét c¸ch tù nhiªn, khi
nã chÞu t¸c ®éng cña träng lùc vµ ®é chªnh nhiÖt ®é, hoÆc do c¸c lùc c−ìng bøc
kh¸c, khi ta dïng b¬m, qu¹t...
C−êng ®é táa nhiÖt, nh− sÏ ®−îc kh¶o s¸t trong ch−¬ng 10, tû lÖ thuËn víi
hÖ sè táa nhiÖt α [w/m2K], vµ ®−îc tÝnh theo c«ng thøc Newton:
q= α (tw - tf)= α∆t
Trong ®ã ∆t lµ hiÖu sè nhiÖt ®é bÒ mÆt vµ chÊt láng.
8.1.3.3. Trao ®æi nhiÖt bøc x¹
Trao ®æi nhiÖt bøc x¹ lµ hiÖn t−îng c¸c ph©n tö vËt 1 bøc x¹ ra c¸c h¹t,
truyÒn ®i trong kh«ng gian d−íi d¹ng sãng ®iÖn tõ, mang n¨ng l−îng ®Õn truyÒn
cho c¸c ph©n tö vËt 2.
Kh¸c víi hai ph−¬ng thøc trªn, trao ®æi nhiÖt bøc x¹ cã thÓ xÈy ra gi÷a hai
vËt ë c¸ch nhau rÊt xa, kh«ng cÇn sù tiÕp xóc trùc tiÕp hoÆc th«ng qua m«i tr−êng
chÊt láng vµ khÝ, vµ lu«n x©y ra víi sù chuyÓn hãa gi÷a n¨ng l−îng nhiÖt vµ n¨ng
92
l−îng ®iÖn tõ. §©y lµ ph−¬ng thøc trao ®æi nhiÖt gi÷a c¸c thiªn thÓ trong vò trô,
ch¼ng h¹n gi÷a mÆt trêi vµ c¸c hµnh tinh. Trªn h×nh (8.1.3) minh ho¹ c¸c ph−¬ng
thøc trao ®æi nhiÖt.
Qu¸ tr×nh trao ®æi nhiÖt thùc tÕ cã thÓ bao gåm 2 hoÆc c¶ 3 ph−¬ng thøc
nãi trªn, ®−îc gäi lµ qu¸ tr×nh trao ®æi nhiÖt phøc hîp. VÝ dô, bÒ mÆt vËt r¾n cã
thÓ trao ®æi nhiÖt víi chÊt khÝ tiÕp xóc nã theo ph−¬ng thøc to¶ nhiÖt vµ trao ®æi
nhiÖt bøc x¹.
8.2. c¸c kh¸i niÖm c¬ b¶n cña truyÒn nhiÖt
8.2.1. Tr−êng nhiÖt ®é
§Ó m« ta ph©n bè nhiÖt ®é trong kh«ng gian theo thêi gian, ta dïng kh¸i
niÖm tr−êng nhiÖt ®é.
Tr−êng nhiÖt ®é lµ tËp hîp tÊt c¶ c¸c gi¸ trÞ nhiÖt ®é tøc thêi trong kho¶ng
thêi gian ®ang xÐt cña mäi ®iÓm trong hÖ vËt kh¶o s¸t.
Gi¸ trÞ nhiÖt ®é tøc thêi t¹i mçi ®iÓm trong kh«ng gian ®−îc x¸c ®Þnh duy
nhÊt nh− mét ®¹i l−îng v« h−íng, do ®ã, tr−êng nhiÖt ®é lµ mét tr−êng v« h−íng.
BiÓu thøc cña tr−êng nhiÖt ®é m« ta luËt ph©n bæ nhiÖt ®é, cho phÐp x¸c
®Þnh gi¸ trÞ nhiÖt ®é tøc thêi t¹i thêi ®iÓm τ theo täa ®é (x,y,z) cña mét ®iÓm bÊt
kú trong hÖ:
t = t(x,y,z,τ).
Theo thêi gian, tr−êng nhiÖt ®é ®−îc ph©n ra hai lo¹i: Kh«ng æn ®Þnh vµ
æn ®Þnh. NÕu gi¸ trÞ nhiÖt ®é tøc thêi t¹i mäi ®iÓm trong hÖ kh«ng thay ®æi theo
thêi gian, tøc 0
t=
τ∂
∂víi mäi (x,y,z) vµ mäi τ, th× tr−êng nhiÖt ®é ®−îc gäi lµ æn
®Þnh: t = t(x,y,z)
NÕu cã mét ®iÓm (x,y,z) t¹i thêi ®iÓm τ khiÕn cho 0
t≠
τ∂
∂
, th× tr−êng nhiÖt
®é ®−îc gäi lµ kh«ng æn ®Þnh.
Tïy theo tÝnh ®èi xøng cña tr−êng sè täa ®é kh«ng gian mµ tr−êng phô
thuéc (th−êng ®−îc gäi lµ sè chiÒu cña tr−êng) cã thÓ lµ 0,1,2,3. VÝ dô, biÓu thøc
cña tr−êng nhiÖt ®é 0, 1, 2, 3 chiÒu cã thÓ lµ:
t = t (τ); t = t (x,τ); t = t(y, z, τ); t = t (x, y, z, τ).
8.2.2. MÆt ®¼ng nhiÖt
T¹i mét thêi ®iÓm cho tr−íc tËp hîp c¸c ®iÓm cã cïng mét gi¸ trÞ nhiÖt ®é
t¶o ra trong kh«ng gian cña tr−êng mét mÆt, ®−îc gäi lµ mÆt ®¼ng nhiÖt.
Ph−¬ng tr×nh cña mÆt ®¼ng nhiÖt lµ: t = f(x,y,z) = const
hay: f(x, y, z) = const
V× nhiÖt ®é tøc thêi t¹i mét ®iÓm lµ duy nhÊt, nªn c¸c mÆt ®¼ng nhiÖt
kh«ng giao nhau.
Trªn mçi mÆt ®¼ng nhiÖt th× t = const, do ®ã nhiÖt ®é chØ thay ®æi theo
h−íng c¾t mÆt ®¼ng nhiÖt.
93
MÆt ®¼ng nhiÖt cã thÓ lµ mÆt cong kÝn hoÆc hë.
8.2.3. Gradient nhiÖt ®é:
XÐt hai mÆt ®¼ng nhiÖt t = const vµ t + dt = const víi dt > 0 nh− h×nh
(8.2.3)
Gäi vËn tèc thay ®æi nhiÖt ®é cña ®iÓm M theo h−íng 1 cho tr−íc lµ
vect¬ τd
dt
l0, trong ®ã 0
1 lµ vect¬ ®¬n vÞ theo h−íng 1, τ∂
∂
t lµ ®¹o hµm tr−êng t
theo h−íng .1
Gäi gradient nhiÖt ®é cña ®iÓm M lµ vËn tèc thay ®æi nhiÖt ®é cña m theo
h−íng ph¸p tuyÕn n cña mÆt ®¼ng nhiÖt t = const, chiÒu tõ nhiÖt ®é thÊp ®Õn
nhiÖt ®é cao.
BiÓu thøc cña vect¬ gradient nhiÖt ®é t¹i ®iÓm M (x,y,z) lµ:
gr adt = .t
z
t
k
y
t
j
x
t
i
n
t
n0∆=
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
§é lín cña vect¬ gradient lµ gradt = ]/[, mK
n
t
∂
∂
.
Vect¬ gr dta m« ta vËn tèc thay ®æi nhiÖt ®é cùc ®¹i ®iÓm M, trªn ph−¬ng
vu«ng gãc mÆt ®¼ng nhiÖt theo chiÒu t¨ng nhiÖt ®é, gi¸ trÞn b»ng n
t
∂
∂.
8.2.4. Vect¬ dßng nhiÖt
§Ó ®Æt tr−ng cho ®é lín vµ ph−¬ng chiÕu dßng nhiÖt truyÒn qua mÆt ®¼ng
nhiÖt ta ®Þnh nghÜa dßng nhiÖt q lµ vect¬ cã ®é lín b»ng l−îng nhiÖt q [w/m2]
truyÒn qua 1m2 mÆt ®¼ng nhiÖt trong mét gi©y, trªn l−íng ph¸p tuyÕn mÆt ®¼ng
nhiÖt theo chiÒu gi¶m nhiÖt ®é:
zyx
0qkqjqiqnq ++=−=
DÊu (-) do vect¬ q ng−îc chiÒu vect¬ gr .dta
Theo lý thuyÕt tr−êng vect¬, l−îng nhiÖt sinh ra trong 1 ®¬n vÞ thÓ tÝch cña
hÖ, tøc hiÖu sè c¸c l−îng nhiÖt ra – vµo 1m2 cña hÖ, lµ:
]./[, 3
zzx mW
z
q
y
q
x
q
qdiv ∂
∂
+
∂
∂
+
∂
∂
=
Do ®ã nÕu div 0q >th× vËt sinh nhiÖt, khi div 0q <th× vËt thu nhiÖt, lóc
div 0q =vËt ®−îc gäi lµ æn ®Þnh nhiÖt.
8.2.5. C«ng suÊt nguån nhiÖt
94
§Ó ®Æt tr−ng c−êng ®é ph¸t nhiÖt t¹i ®iÓm M cña vËt V, ta ®Þnh nghÜa n¨ng
suÊt ph¸t nhiÖt cña ®iÓm M (x,y,z) lµ tû sè ]/[, 3
vmW
dV
Q
q
∂
=trong ®ã ][WQ∂ lµ
c«ng suÊt nhiÖt ph¸t ra tõ ph©n tè thÓ tÝch dV[m3] bao quanh ®iÓm.
NÕu biÕt qv = qv (xy,z) th× tÝnh ®−îc c«ng suÊt ph¸t nhiÖt cña nguån V
theo:
,VdqQ
v
v
∫
=
Khi nguån nhiÖt ph©n bè ®Òu, qv = const, th× Q = qvV.