68
ø
CHÖÔNG 7
CAÙC MAÙY PHAÙT ÑIEÄN MOÄT CHIEÀU
§ 7.1. Ñaïi cöông
Treân thöïc teá caùc traïm phaùt ñieän hieän ñaïi chæ phaùt ra ñieän naêng xoay chieàu 3
pha, phaàn lôùn naêng löôïng ñoù ñöôïc duøng döôùi daïng ñieän xoay chieàu trong coâng
nghieäp, ñeå thaép saùng vaø duøng cho caùc nhu caàu trong ñôøi soáng. Trong nhöõng tröôøng
hôïp do ñieàu kieän saûn xuaát baét buoäc phaûi duøng ñieän 1 chieàu (xí nghieäp hoùa hoïc,
coâng nghieäp luyeän kim, giao thoâng vaän taûi v.v…) thì ngöôøi ta thöôøng bieán ñieän xoay
chieàu thaønh moät chieàu nhôø caùc boä chænh löu hoaëc chænh löu kieåu maùy ñieän, caùch
thöù hai laø duøng maùy phaùt ñieän moät chieàu ñeå laø nguoàn ñieän moät chieàu.
Phaân loaïi caùc maùy phaùt ñieän moät chieàu theo phöông phaùp kích thích. Chuùng
ñöôïc chia thaønh:
a.Maùy phaùt ñieän moät chieàu kích thích ñoäc laäp.
b.Maùy phaùt ñieän moät chieàu töï kích
Trong ñoù:
-Maùy phaùt ñieän moät chieàu kích thích ñoäc laäp goàm
+ Maùy phaùt ñieän moät chieàu kích thích baèng ñieän töø: duøng nguoàn DC, aéc
qui... v.v.
+ Maùy phaùt ñieän moät chieàu kích thích baèng nam chaâm vónh cöûu.
- Theo caùch noái daây quaán kích thích, caùc maùy phaùt ñieän moät chieàu töï kích
ñöôïc chia thaønh:
+ Maùy phaùt ñieän moät chieàu kích thích song song
+ Maùy phaùt ñieän moät chieàu kích thích noái tieáp
+ Maùy phaùt ñieän moät chieàu kích thích hoãn hôïp
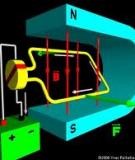
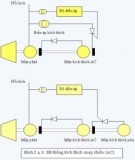
Hình 7.1 Sô ñoà nguyeân lyù cuûa maùy phaùt ñieän moät chieàu
It
Iö
Iö
Iö
Iö
UtItIt
69
ø
§ 7.2. Caùc ñaëc tính cô baûn cuûa caùc MFÑDC
Baûn chaát cuûa maùy phaùt ñieän ñöôïc phaân tích nhôø nhöõng ñaëc tính quan heä giöõa
4 ñaïi löôïng cô baûn cuûa maùy :
- Ñieän aùp ñaàu cöïc maùy phaùt ñieän: U
- Doøng ñieän kích töø : I
t
- Doøng ñieän phaàn öùng I
ö
- Toác ñoä quay : n
Trong ñoù n = C
te
coøn 3 ñaïi löôïng taïo ra moái quan heä chính vaø caùc ñaëc tính chính laø:
c
Ñaëc tính phuï taûi (ñaëc tính taûi): U = f(I
t
) khi I = I
ñm
= C
te
, n = n
ñm
= C
te
. Khi
I = 0 ñaëc tính phuï taûi chuyeån thaønh ñaëc tính khoâng taûi U
o
= E
o
= f(I
t
). Ñaëc tính naøy
coù yù nghóa quan troïng trong vieäc ñaùnh giaù maùy phaùt vaø ñeå veõ caùc ñaëc tính khaùc
cuûa maùy phaùt ñieän.
d
Ñaëc tính ngoaøi: U = f(I) khi R
ñc
= C
te
(I
t
= C
te
)
e
Ñaëc tính ñieàu chænh : I
t
= f(I) khi U = C
te
. Trong tröôøng hôïp rieâng khi U =
0, ñaëc tính ñieàu chænh chuyeån thaønh ñaëc tính ngaén maïch I
t
= f(I
n
).
Chuùng ta haõy xeùt caùc ñaëc tính cuûa maùy phaùt ñieän theo phöông phaùp kích töø vaø coi
ñoù laø nhaân toá chuû yeáu ñeå xaùc ñònh caùc baûn chaát cuûa caùc maùy phaùt ñieän.
§ 7.2.1 Caùc ñaëc tính cuûa maùy phaùt ñieän kích thích ñoäc laäp
1. Ñaëc tính khoâng taûi
U
o
= f(I
t
) khi I = 0 vaø n = C
te
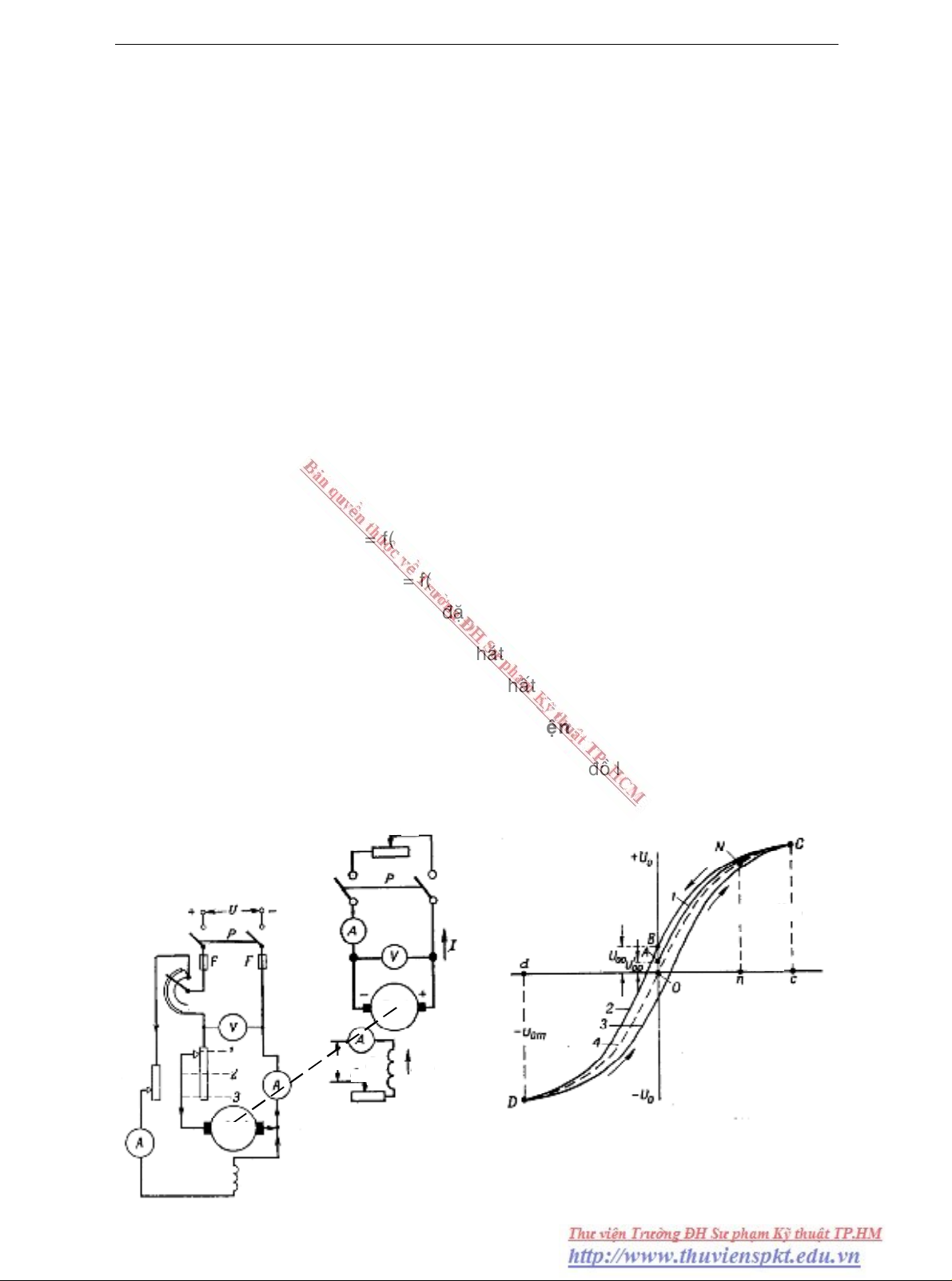
. sô ñoà laáy ñaëc tính ñoù trình baøy
treân hình 7-2a, ñaëc tính ñöôïc bieåu thò treân h7-2b.
Hình 7.2 Sô ñoà laáy caùc ñaëc tính vaø ñaëc tính khoâng taûi cuûa MFÑMCKTÑL
Rt
ItRñc
Ut
Uñm + U0max
- It+ It
ab
Rñc
Rmm
Rñc
It
IöÑ
KT
Iö
→
→
70
ø
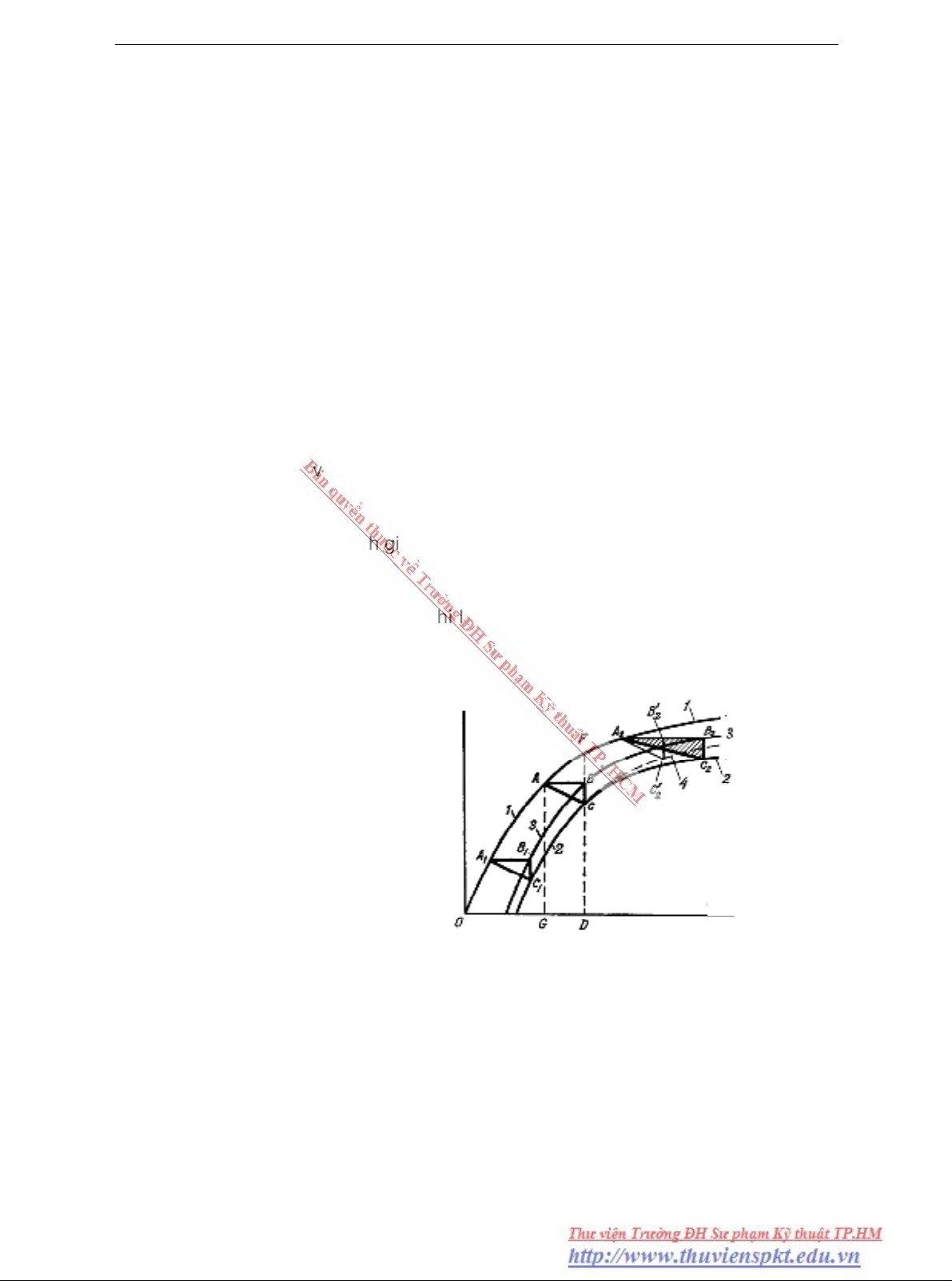
Vì trong maùy thöôøng coù töø thoâng dö neân khi I
t
= 0 treân cöïc cuûa maùy phaùt coù ñieän
aùp U
/oo
= OA (h7-2b), thöôøng U
/oo
= (2 ÷ 3)% U
ñm
. Khi bieán ñoåi I
t
töø I
t
= 0 ÷ +I
tmax
=
OC ñieän aùp U seõ taêng theo ñöôøng cong 1 ñeán + U
omax
= Cc. Thöôøng U
omax
= (1,1 ÷
1,25) U
ñm
. Luùc khoâng taûi phaàn öùng cuûa MFÑKTÑL chæ noái vôùi voltmet neân :
U
o
= E
o
= C
e
.n.Φ = C’
e
.Φ
Neân quan heä U
o
= f(I
t
) laëp laïi quan heä Φ = f(I
t
) theo 1 thöôùc tæ leä nhaát ñònh.
Baây giôø chuùng ta haõy bieán ñoåi I
t
töø + I
tmax
= OC ÷ I
t
= 0 sau ñoù ñoåi noái ngöôïc
chieàu doøng ñieän trong maïch kích thích roài tieáp tuïc bieán ñoåi I
t
töø I
t
= 0 ÷ - I
tmax
= Od
→ veõ ñöôïc ñöôøng cong 2.
Laëp laïi söï bieán ñoåi cuûa doøng ñieän theo thöù töï ngöôïc laïi töø – I
tmax
= Od ÷
+I
tmax
= OC thì ta veõ ñöôïc ñöôøng 3.
Ñöôøng cong 3 vaø 2 taïo thaønh chu trình töø treã xaùc ñònh tính chaát theùp cuûa
cöïc töø vaø goâng töø.
Veõ ñöôøng 4 trung bình giöõa caùc ñöôøng treân chuùng ta ñöôïc ñaëc tính khoâng
taûi ñeå tính toaùn.
2. Caùc ñaëc tính phuï taûi
U = f(I
t
) khi I = C
te
, n = C
te
.
Khi MF coù doøng ñieän taûi I thì ñieän
aùp treân ñaàu cöïc bò haï thaáp do :
- Ñieän aùp rôi treân phaàn öùng I
ö
R
ö
.
- Phaûn öùng phaàn öùng ε.
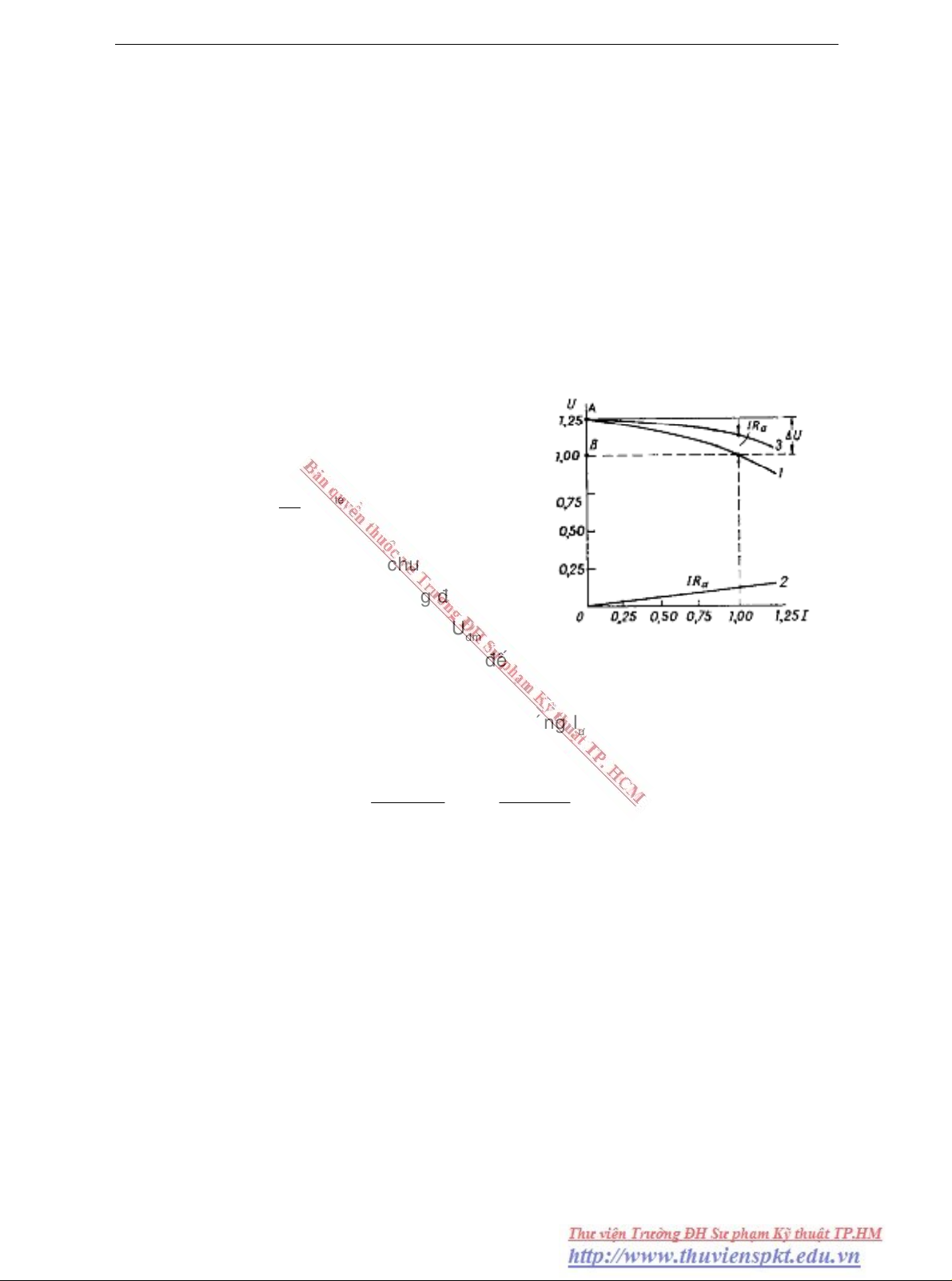
Caùc ñöôøng 1, 2 treân h7-3
bieåu thò caùc ñaëc tính khoâng taûi vaø
phuï taûi. Neáu coäng theâm ñieän aùp
rôi I
ö
R
ö
vaøo ñöôøng cong phuï taûi thì
ta coù ñaëc tính phuï taûi trong
U + I
ö
R
ö
= E
ö
= f(I
t
)
Hình 7.3 Ñaëc tính phuï taûi cuûa MFÑDCKTÑL
Khi I = C
te
, n = C
te
laø ñöôøng cong 3.
Ñaëc tính phuï taûi cuøng vôùi ñaëc tính khoâng taûi cho pheùp thaønh laäp ∆ ñaëc tính
cuûa maùy phaùt ñieän moät chieàu. Tam giaùc naøy moät maët cho pheùp ñaùnh giaù aûnh
höôûng cuûa ñieän aùp rôi vaø phaûn öùng phaàn öùng ñoái vôùi ñieän aùp cuûa maùy phaùt ñieän
moät chieàu maët khaùc coù theå duøng ñeå veõ ñaëc tính ngoaøi vaø ñaëc tính ñieàu chænh cuûa
maùy phaùt ñieän moät chieàu.
Iö = Cte
Iö = 0
→I
t
→
U
71
ø
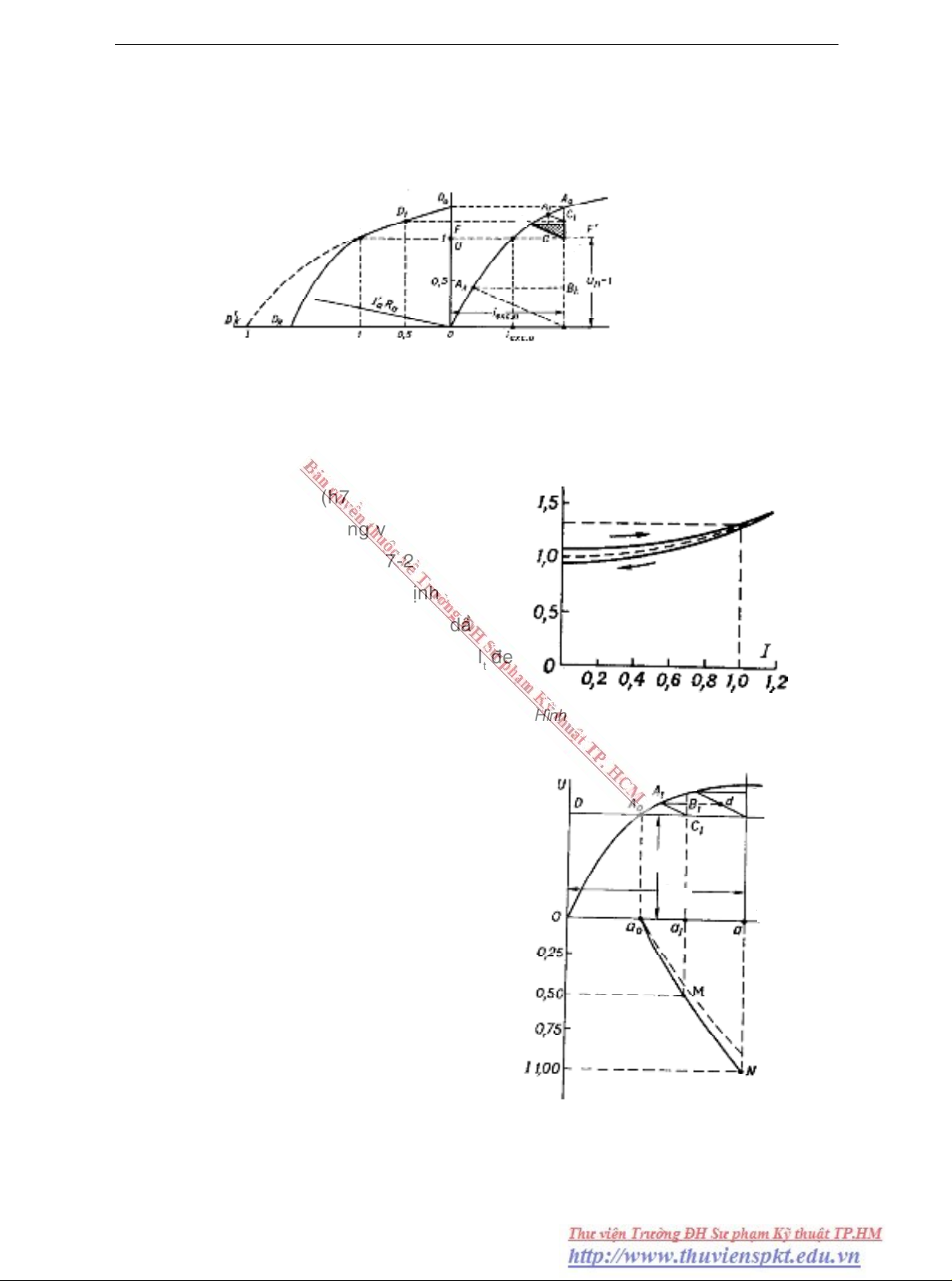
Caùch veõ ∆ ñaëc tính nhö sau : Qua ñieåm D laáy tuøy yù treân truïc hoaønh, veõ 1 ñöôøng
thaúng // vôùi truïc tung caét caùc ñöôøng cong 2, 3 vaø 1 ôû caùc ñieåm C, B vaø F. Theo
caùch veõ ñoù ñoaïn BC = I
ö
R
ö
. Luùc khoâng taûi vôùi I
t
= OD ta coù U
o
= FD cho neân toaøn
boä ñieän aùp rôi CF khi coù doøng ñieän taûi I seõ lôùn hôn ñieän aùp rôi BC = I
ö
R
ö
1 trò soá BF
do phaûn öùng phaàn öùng sinh ra. Luùc khoâng taûi E
ö
= BD = AG laø do doøng ñieän I
to
=
OG sinh ra coù trò soá nhoû hôn OD 1 ñoaïn DG = OD – OG. Töø ñoù ta thaáy trò soá S.t.ñ
phaûn öùng phaàn öùng bieåu thò theo thöôùc ño doøng ñieän kích thích baèng GD. Ñeå veõ
ñöôïc ∆ ñaëc tính chæ caàn keû qua B 1 ñoaïn BA = GD // vôùi truïc hoaønh.
3. Ñaëc tính ngoaøi
U = f(I) khi I
t
= C
te
(R
ñc
= C
te
) , n = C
te
.
Ñaëc tính ngoaøi ñöôïc laáy theo sô ñoà 7-2a luùc
caàu dao P ñöôïc ñoùng maïch. Ñieän aùp U
t
treân
ñaàu cöïc kích thích ñöôïc giaû thieát laø khoâng lôùn,
do ñoù :
Ñeå laáy ñaëc tính ngoaøi chuùng ta quay
MFÑ ñeán n = n
ñm
vaø thieát laäp doøng ñieän kích
thích I
tñm
sao cho I = I
ñm
= 1 vaø U = U
ñm
= 1
(h7-4). Sau ñoù giaûm daàn phuï taûi cuûa MFÑ ñeán
khoâng taûi. Ñieän aùp cuûa MFÑ taêng theo ñöôøng
Hình 7.4 Ñaëc tính ngoaøi cuûa MFÑDCKTÑL
cong 1 vì phuï taûi giaûm ñieän aùp rôi treân phaàn öùng I
ö
R
ö
vaø phaûn öùng phaàn öùng
giaûm luùc khoâng taûi U
o
= OA, do ñoù :
Vì R
ö
= C
te
neân I
ö
R
ö
= f(I
ö
) bieåu dieãn baèng ñöôøng thaúng 2.
Ñöôøng cong 3 laø quan heä cuûa U + I
ö
R
ö
= E
ö
= f(I
ö
) goïi laø ñaëc tính trong cuûa
maùy phaùt ñieän.
Töø ñaëc tính khoâng taûi U
o
= f(I
t
) vaø ∆ ñaëc tính veõ ñaëc tính ngoaøi vôùi giaû thieát
caùc caïnh cuûa ∆ bieán ñoåi tæ leä vôùi doøng ñieän I.
Tröôùc heát ta laáy U
ñm
= 1 veõ treân ñoà thò ∆ A
ñm
B
ñm
C
ñm
töông öùng vôùi I
ñm
= 1
sao cho ñænh A
ñm
naèm treân ñöôøng ñaëc tính khoâng taûi, coøn caïnh A
ñm
B
ñm
vaø B
ñm
C
ñm
song song vôùi truïc hoaønh vaø truïc tung, vò trí cuûa ñieåm C
ñm
xaùc ñònh baèng caùch ño
töông öùng vôùi ñieän aùp U
ñm
= 1. Keùo daøi caïnh B
ñm
C
ñm
ta ñöôïc I
tñm
= OCn = 1 vaø
ñieåm A
o
töông öùng ñieän aùp khoâng taûi U
o
. Ta ñem ñieåm C
ñm
sang beân traùi truïc tung
ñöôïc ñieåm D
ñm
töông öùng vôùi doøng ñieän I
ñm
= 1 coøn
te
t
t
tC
R
U
I==
100
U
UU
100
OB
OBOA
U
ñm
ñm0 −
=
−
=∆ %
72
ø
ñieåm AI thì ñeán ñieåm D
o
treân truïc ñöùng.
Ñeå coù ñaëc tính ngoaøi töông öùng vôùi I = ½I
ñm
thì ∆ ñaëc tính coù caùc caïnh = ½ caùc
caïnh ∆ A
ñm
B
ñm
C
ñm
.
Bñm
Cñm
Añm
Dñm
Cn It
Hình 7.5 Döïng ñaëc tính ngoaøi cuûa MFÑKTÑL
töø ñaëc tính khoâng taûi vaø tam giaùc ñaëc tính
4. Ñaëc tính ñieàu chænh
I
t
= f(I) khi U = C
te
, n = C
te
I
t
Itñm
It
Añm Bñm
Cñm
Uñm=1
Hình 7.6 Ñaëc tính ñieàu chænh cuûa MFÑKTÑL
Hình 7.7 Döïng ñaëc tính ñieàu chænh cuûa
MFÑKTÑL töø ñaëc tính khoâng taûi vaø tam giaùc
ñaëc tính
Vì khi I
t
= C
te
thì U treân cöïc maùy phaùt haï thaáp
khi I taêng vaø ngöôïc laïi (h7-4). Neáu muoán U =
C
te
thì phaûi taêng I
t
khi I taêng vaø
giaûm I
t
khi I
giaûm. Sô ñoà thí nghieäm nhö h7-2a, cho maùy
phaùt laøm vieäc vaø mang taûi ñeán ñònh möùc I =
I
ñm
, U = U
ñm
, I
t
= I
tñm
sau ñoù giaûm daàn taûi
nhöng phaûi giöõ cho n = C
te
vaø ñieàu chænh I
t
ñeå
cho U = U
ñm
laàn löôït ghi caùc trò soá cuûa I vaø I
t
ta
coù daïng ñaëc tính ñieàu chænh nhö h7-6.
Xaây döïng ñaëc tính ñieàu chænh baèng ñaëc tính
khoâng taûi vaø ∆ ñaëc tính : vôùi vò trí xaùc ñònh U
o
= U
ñm
= 1 = Aoao khi I = 0 ta ñöôïc ñieåm ao
töông öùng vôùi I
to
= oao. Neáu ñaët 1 = ∆
A
ñm
B
ñm
C
ñm
töông öùng vôùi taûi I = I
ñm
sao cho
ñieåm A
ñm
naèm treân ñöôøng ñaëc tính khoâng taûi
vaø ñænh C
ñm
naèm treân ñöôøng thaúng DC öùng
vôùi U = U
ñm
= C
te
. Haï ñöôøng thaúng ñöùng B
ñm
C
ñm
ta ñöôïc I
tñm
= oa töông öùng vôùi Iñm ta ñöôïc
ñieåm N.Muoán coù ñieåm M töông öùng vôùi I = ½
I
ñm
thì caùc caïnh cuûa ∆A
1
B
1
C
1
= ½ caùc caïnh
cuûa ∆ A
ñm
B
ñm
C
ñm
vôùi ñieåm A
1
tröôït treân ñöôøng
ñaëc tính khoâng taûi, C
1
tröôït treân ñöôøng DC.
Noái 3 ñieåm aoMN ta ñöôïc ñaëc tính ñieàu chænh.





![Sổ giáo án thực hành Máy DVD Trần Duy Khánh [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2017/20170313/kakavt20/135x160/8341489413963.jpg)