106
1
pϖ
11
H1v1
pϖn
Hn
n
vn
n
pϖ2
H
2
2
v
2
2
Tråí khaïng thuíy læûc täøng cuía âæåìng äúng laì Σ∆p
Theo âënh luáût Becnuli ta coï :
H1 + ρω21 /2 = Hn + ρω2n /2 + Σ∆p (6-4)
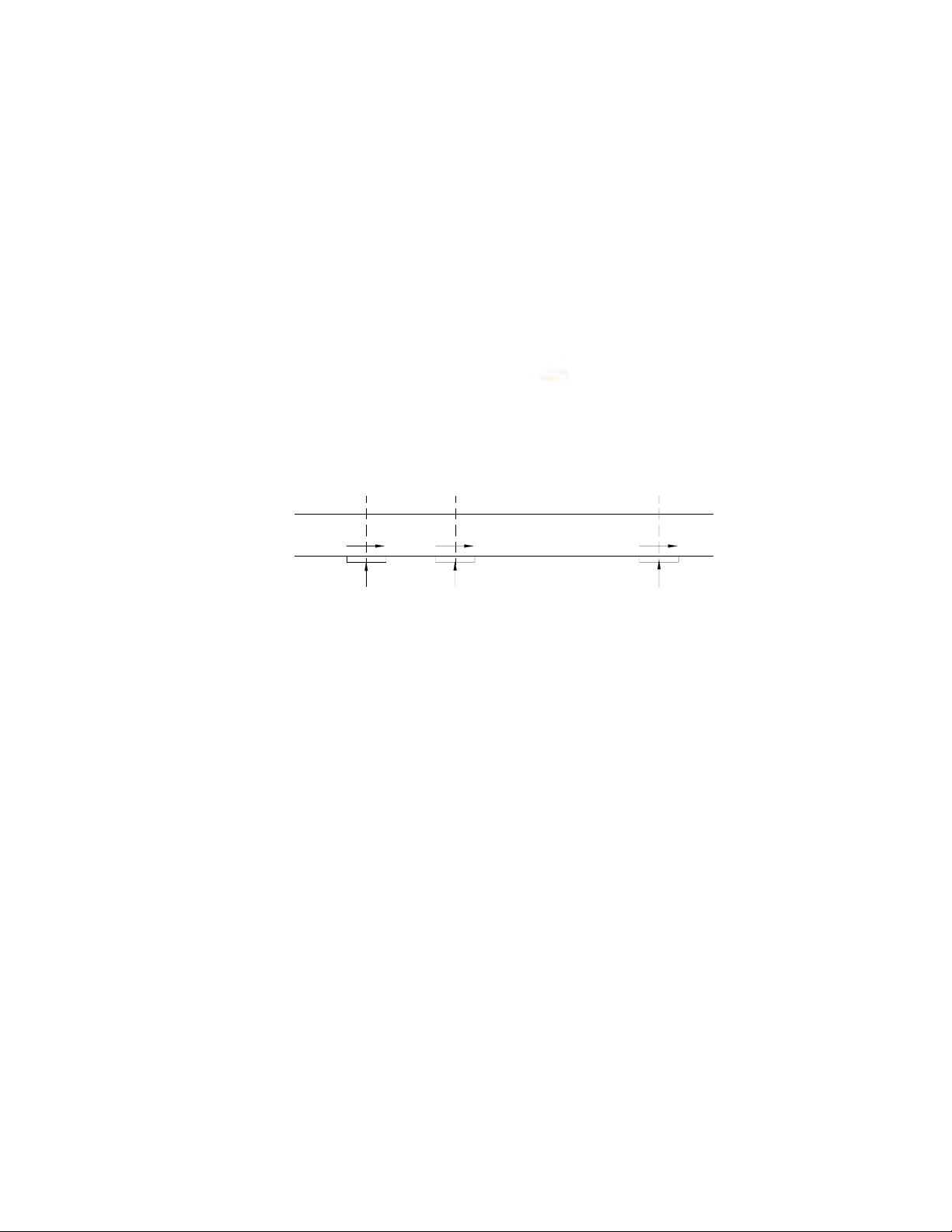
Hçnh 6.2 : Phán bäú cäüt aïp ténh doüc theo kãnh gioï
Hay:
Hn = H1 + ρ(ω21 - ω2n)/2 - Σ∆p
Tæì âoï suy ra :
∆H = Hn - H1 = ρ(ω21 - ω2n)/2 - Σ∆p (6-5)
Thaình pháön ρ(ω21 - ω2n)/2 goüi laì âäü giaím cäüt aïp âäüng.
Nhæ váûy âãø duy trç cäüt aïp ténh trãn tuyãún äúng khäng âäøi ∆H =0 ta phaíi thiãút kãú hãû thäúng
kãnh gioï sao cho ρ(ω21 - ω2n)/2 - Σ∆p = 0
Ta coï caïc træåìng håüp coï thãø xaîy ra nhæ sau:
a) Træåìng håüp
ρ
(
ω
21 -
ω
2n)/2 =
Σ∆
p : Giaím cäüt aïp âäüng bàòng täøng täøn tháút trãn tuyãún
äúng.
Nhæ váûy cäüt aïp âäüng âaî biãún mäüt pháön âãø buì vaìo täøn tháút trãn tuyãún äúng.
Khi âoï : H1 = Hn nghéa laì cäüt aïp ténh khäng thay âäøi doüc theo âæåìng äúng. Âáy laì træåìng
håüp lyï tæåíng, täúc âäü vaì læu læåüng åí caïc miãûng thäøi seî âãöu nhau.
b) Træåìng håüp
ρ
(
ω
21 -
ω
2n)/2 >
Σ∆
p hay H1 < Hn
Giaím cäüt aïp âäüng låïn hån täøng täøn tháút aïp læûc trãn tuyãún äúng.
Trong træåìng håüp naìy ta coï Hn > H1 , pháön cäüt aïp âäüng dæ thæìa goïp pháön laìm tàng cäüt aïp
ténh cuäúi âæåìng äúng, læåüng læåüng gioï caïc miãûng thäøi cuäúi låïn hån, hay gioï däön vaìo cuäúi
tuyãún äúng.
Træåìng håüp naìy coï thãø xaîy ra khi :
- Täúc âäü âoaûn âáöu quaï låïn, nãn aïp suáút ténh trãn trong äúng ráút nhoí trong khi täúc âäü âoaûn
cuäúi nhoí. Trong mäüt säú træåìng håüp nãúu täúc âäü âi ngang qua tiãút diãûn nåi làõp caïc miãûng thäøi åí
âoaûn âáöu quaï låïn thç caïc miãûng thäøi âáöu coï thãø tråí thaình miãûng huït luïc âoï taûo nãn hiãûn tæåüng
huït kiãøu EJectå. Âãø khàõc phuûc, cáön giaím täúc âäü âoaûn âáöu, tàng täúc âäü âoaûn cuäúi. Vç thãú khi
læu læåüng doüc theo kãnh gioï giaím thç phaíi giaím tiãút diãûn tæång æïng âãø duy trç täúc âäü gioï,
traïnh khäng nãn âãø täúc âäü giaím âäüt ngäüt .
- Âæåìng äúng ngàõn, êt tråí læûc cuûc bäü nhæng coï nhiãöu miãûng thäøi hoàûc âoaûn reí nhaïnh.
Træåìng håüp naìy tråí læûc Σ∆p ráút nhoí, nhæng täúc âäü giaím nhanh theo læu læåüng. Âãø khàõc phuûc
cáön giaím nhanh tiãút diãûn âoaûn cuäúi nhàòm khäúng chãú täúc âäü phuì håüp.
c) Træåìng håüp
ρ
(
ω
21 -
ω
2n)/2 <
Σ∆
p hay H1 > Hn
Giaím cäüt aïp âäüng nhoí hån täøng täøn tháút aïp læûc trãn tuyãún äúng.
Trong træåìng håüp naìy gioï táûp trung vaìo âáöu tuyãún äúng.
107
ϖ
p
ϖ
p1
H1
1
v1v
H2
22
2
12
ϖ
p
Hn
nn
vn
n
Nguyãn nhán gáy ra coï thãø laì:
- Täúc âäü âoaûn âáöu nhoí, aïp suáút ténh låïn nãn læu læåüng gioï cuía caïc miãûng thäøi âáöu låïn vaì
cuäúi tuyãún äúng læu læåüng khäng âaïng kãø.
- Täøn tháút âæåìng äúng quaï låïn : Âæåìng äúng quaï daìi, coï nhiãöu chäø khuïc khuyíu.
- Tiãút diãûn âæåìng äúng âæåüc giaím quaï nhanh khäng tæång æïng våïi mæïc âäü giaím læu læåüng
nãn täúc âäü doüc theo tuyãún äúng giaím êt, khäng giaím tháûm chê coìn tàng. Vç thãú cäüt aïp ténh âáöu
tuyãún äúng låïn hån cuäúi tuyãún äúng.
Vç váûy khi thiãút kãú âæåìng äúng cáön phaíi chuï yï :
- Thiãút kãú giaím dáön tiãút diãûn âæåìng äúng doüc theo chiãöu thäøi mäüt caïch håüp lyï , tuyì thuäüc
vaìo tråí læûc cuía âæåìng äúng.
4) Sæû phán bäú cäüt aïp ténh trãn âæåìng äúng huït.
Xeït mäüt kãnh huït, täúc âäü trung bçnh vaì cäüt aïp ténh cuía doìng khäng khê taûi tiãút diãûn coï
miãûng huït âáöu laì ω1 vaì H1 , cuía miãûng huït thæï 2 laì ω2 vaì H2 ... vaì cuía miãûng huït thæï n laì ωn
vaì Hn .
Tråí khaïng thuíy læûc täøng cuía âæåìng äúng laì Σ∆p
Hçnh 6.3 : Phán bäú cäüt aïp ténh doüc theo kãnh huït
Theo âënh luáût Becnuli ta coï :
H1 + ρω21 /2 = Hn + ρω2n /2 + Σ∆p
Hay:
Hn = H1 + ρ(ω21 - ω2n)/2 - Σ∆p
Hay :
∆H = Hn - H1 = ρ(ω21 - ω2n)/2 - Σ∆p (6-6)
Âãø ∆H = 0 ta phaíi âaím baío : ρ(ω21 - ω2n)/2 - Σ∆p = 0
Hay noïi caïch khaïc täúc âäü gioï doüc theo chiãöu chuyãøn âäüng cuía doìng khäng khê phaíi giaím
dáön vaì mæïc âäü giaím phaíi tæång æïng våïi mæïc tàng täøn tháút Σ∆p.
Do læu læåüng doüc theo chiãöu chuyãøn âäüng cuía gioï trong kãnh huït tàng dáön vaì täúc âäü gioï
cuîng phaíi giaím dáön , vç thãú tiãút diãûn kãnh huït phaíi låïn dáön.
6.1.2.2 Mäüt säú váún âãö liãn quan tåïi thiãút kãú âæåìng äúng gioï
1) Læûa choün täúc âäü khäng khê trãn âæåìng äúng
Læûa choün täúc âäü gioï coï liãn quan tåïi nhiãöu yãúu täú.
- Khi choün täúc âäü cao âæåìng äúng nhoí, chi phê âáöu tæ vaì váûn haình tháúp, nhæng tråí læûc hãû
thäúng låïn vaì âäü äön do khê âäüng cuía doìng khäng khê chuyãøn âäüng cao.
- Ngæåüc laûi khi täúc âäü beï, âæåìng äúng låïn chi phê âáöu tæ vaì váûn haình låïn, khoï khàn làõp âàût,
nhæng tråí læûc beï.
108
Täúc âäü håüp lyï laì mäüt baìi toaïn kinh tãú, kyî thuáût phæïc taûp. Baíng 6.3 dæåïi âáy trçnh baìy
täúc âäü gioï thêch håüp duìng âãø tham khaío læûa choün khi thiãút kãú.
Baíng 6.3 : Täúc âäü gioï trãn kãnh gioï, m/s
Bçnh thæåìng
ÄÚng cáúp ÄÚng nhaïnh
Khu væûc Âäü äön nhoí
ÄÚng âi ÄÚng vãö ÄÚng âi ÄÚng vãö
- Nhaì åí 3 5 4 3 3
- Phoìng nguí
- Phoìng nguí k.s vaì bãûnh viãûn
5 7,6 6,6 6 5
- Phoìng laìm viãûc
- Phoìng giaïm âäúc
- Thæ viãûn
6 10,2 7,6 8,1 6
- Nhaì haït
- Giaíng âæåìng
4 6,6 5,6 5 4
- Vàn phoìng chung
- Nhaì haìng, cæía haìng cao cáúp
- Ngán haìng
7,6 10,2 7,6 8,1 6
- Cæía haìng bçnh thæåìng
- Cafeteria
9,1 10,2 7,6 8,1 6
- Nhaì maïy, xê nghiãûp, phán x 12,7 15,2 9,1 11,2 7,6
2) Xaïc âënh âæåìng kênh tæång âæång cuía âæåìng äúng
Âãø váûn chuyãøn khäng khê ngæåìi ta sæí duûng nhiãöu loaûi äúng gioï: Chæî nháût, vuäng, ä van,
troìn. Tuy nhiãn âãø tênh toaïn thiãút kãú âæåìng äúng gioï thäng thæåìng ngæåìi ta xáy dæûng caïc giaîn
âäö cho caïc äúng dáùn troìn. Vç váûy cáön qui âäøi tiãút diãûn caïc loaûi ra tiãút diãûn troìn tæång âæång,
sao cho täøn tháút aïp suáút cho mäüt âån vë chiãöu daìi âæåìng äúng laì tæång âæång nhau, trong âiãöu
kiãûn læu læåüng gioï khäng thay âäøi.
Âæåìng kênh tæång âæång coï thãø xaïc âënh theo cäng thæïc hoàûc tra baíng. Âãø thuáûn låüi cho
viãûc tra cæïu vaì læûa choün , ngæåìi ta âaî láûp baíng xaïc âënh âæåìng kênh tæång âæång cuía caïc
âæåìng äúng daûng chæî nháût nãu åí baíng 6-4.
- Âæåìng kênh tæång âæång cuía tiãút diãûn chæî nháût âæåüc xaïc âënh theo cäng thæïc sau :
a, b laì caûnh chæî nháût, mm
Tuy täøn tháút giäúng nhau nhæng tiãút diãûn trãn 2 äúng khäng giäúng nhau
S' = a x b > S = π x dtâ2 / 4
- Âæåìng kênh tæång âæång cuía äúng ä van:
mm
ba
ba
dtd ,
)(
).(
.3,1 25,0
625,0
+
=(6-7)
(6-8)
109
A - Tiãút diãûn äúng ä van :
A = π x b2 / 4 + b(a-b)
a, b laì caûnh daìi vaì caûnh ngàõn cuía ä van, mm
p Laì chu vi màût càõt : p = π.b + 2(a-b), mm
25,0
625,0
.55,1 p
A
dtd =