HỒI QUI VỚI BIẾN GIẢ VÀ BIẾN BỊ CHẶN
Bản chất của biến giả -Biến giả cho sự thay đổi
trong hệ số chặn
Biến giả cho sự thay đổi trong hệ số góc
Biến giả và Kiểm định tính ổn định cấu trúc của mô
hình
Hồi qui tuyến tính từng khúc
Biến phụ thuộc là biến giả
Mô hình xác suất tính tuyến tính (LPM)
Mô hình Probit và Logit
Biến bị chặn: mô hình Tobit
Bản chất của biến giả -Biến giả cho sự thay
đổi trong hệ số chặn
Trong phân tích hồi qui, có 2 loại biến chính: biến định
lượng và biến định tính.
Các biến định lượng: giá trị của những quan sát đó
là những con số.
Biến định tính thường biểu thị có hay không có một
tính chất hoặc biểu thị các mức độ khác nhau của
một tiêu thức thuộc tính nào đó, chẳng hạn như
giới tính, tôn giáo, chủng tộc, nơi cư trú, …
Những biến định tính này cũng có sự ảnh hưởng
đối với biến phụthuộc và phải được đưa vào mô
hình hồi quy.
Bản chất của biến giả -Biến giả cho sự thay
đổi trong hệ số chặn
Biến giả (D) thường có 2 giá trị:
D = 1: nếu quan sát có một thuộc tính nào đó, và
D = 0: nếu không có thuộc tính đó.
Biến giảcũng được đưa vào mô hình hồi
quy giống nhưmột biến định lượng,
Chúng được dùng đểchỉsựkhác biệt giữa 2
nhóm quan sát: có và không có một thuộc
tính nào đó.
Bản chất của biến giả -Biến giả cho sự thay
đổi trong hệ số chặn
Ví dụ: giảsửta muốn xem có sựkhác biệt nào
không vềtiền công giữa nam và nữvới những điều
kiện vềcông việc nhưnhau.
Hàm hồi quy ngẫu nhiên cho một quan sát:
wagei= 0+ 1Di+ ’X+ ui,
Trong đó D là biến giảvềgiới tính: D = 1 nếu là nam
và 0 nếu là nữ; Xlà vector chỉnhững đặc điểm cá
nhân và công việc.
Nếu D=1: wagei= 0+ 1+ ’X+ ui,
Nếu D=0: wagei= 0+ ’X+ ui,
Vậy hệsố1đo lường sựkhác biệt của hệsố0
giữa nhóm nam và nữ.
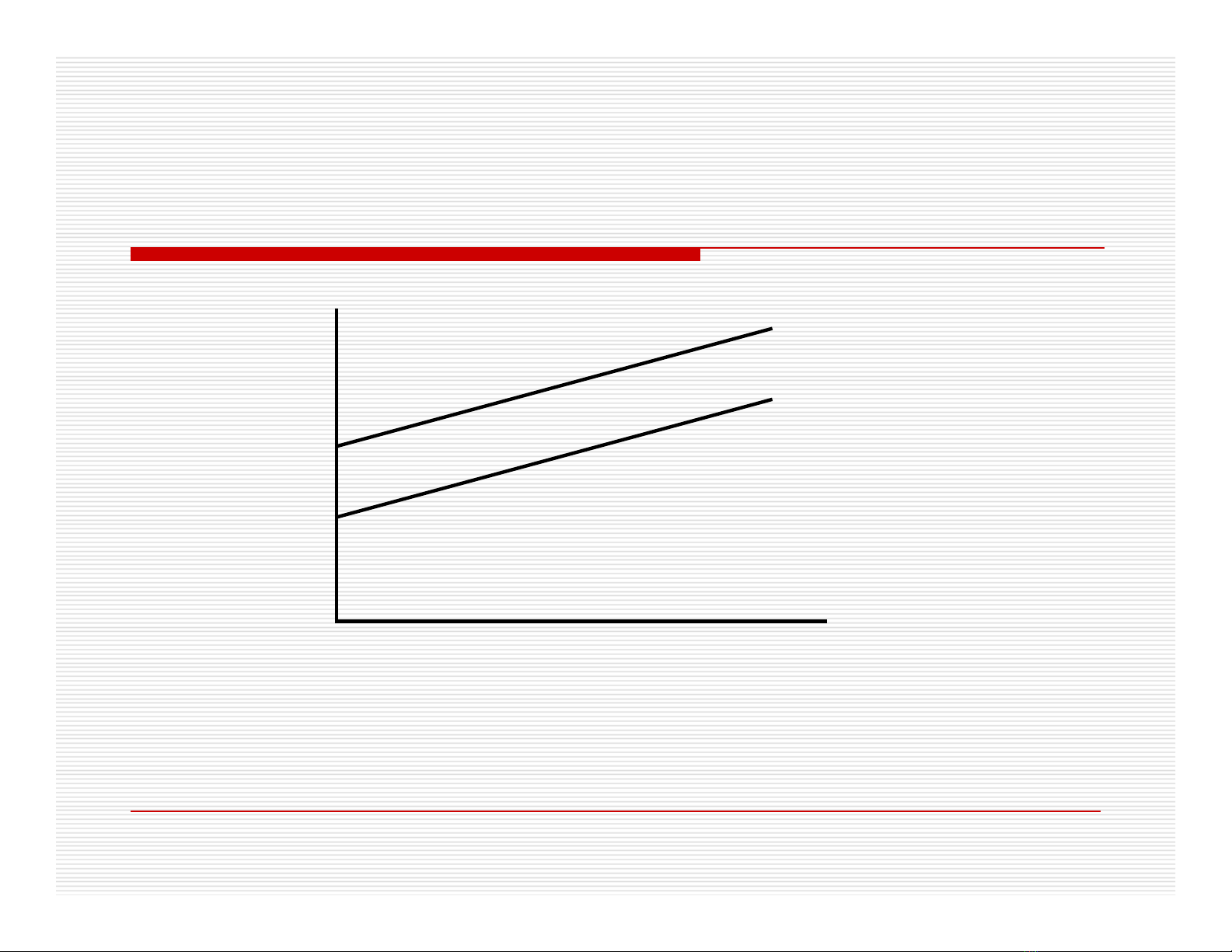
Biến giả cho sự thay đổi trong hệ số chặn
(hệ số tự do)
y
x
Hình 7.1 Đường hồi qui với hệ số góc giống nhau
và hệ số chặn khác nhau
Wagei= 0+ 1+ ’X+ ui
Wagei= 0+ ’X+ ui