S GIÁO D C & ĐÀO T OỞ Ụ Ạ
QU NG NAMẢ
K THI CH N H C SINH GI I L P 12 THPTỲ Ọ Ọ Ỏ Ớ
NĂM H C 2012 – 2013Ọ
H NG D N CH M MÔN TOÁN 12 THPTƯỚ Ẫ Ấ
Câu N i dung l i gi iộ ờ ả Điể
m
1 3.0
( )( )
2 2
1
ln ln 1 (1)
2
1 (2)
x y xy y x
x y
− = + −
+ =
3.0
+ĐK: x,y >0
(1) lnx – lny = ( y – x)(xy + 1)
= ( y – x)(xy + x2 + y2 ) (do (2))
= y3 – x3
lnx + x3= lny + y3 (3)
Xét hàm s f(t) = lnt + tố3, Df = (0; +∞)
Ta có : f’(t) =
2
13 0,
f
t t D
t+ > ∀
=> f là hàm s tăng trên Dốf
Do đó : (3) x = y (do f đn đi u)ơ ệ
Suy ra: (2)
2
1
2
x=
x =
2
2
(Vì x >0)
=> x = y =
2
2
là nghi m c a h ph ng trình.ệ ủ ệ ươ
V y h ph ng trình đã cho có 1 nghi m (x; y)ậ ệ ươ ệ :
2 2
;
2 2
� �
� �
� �
� �
0.5
0.25
0.5
0.5
0.5
0.25
0.5
2 2.5
T gi thi t ta có: xừ ả ế n+1 – xn = - xn2 ≤ 0
=> ...≤xn ≤ xn -1 ≤....≤ x2 ≤ x1= a
Căn c vào đ th hàm s y = f(x) = x(1 – x) và t p nh c a các mi n t ng ngứ ồ ị ố ậ ả ủ ề ươ ứ
qua ánh x x ạ
a
x(1-x), ta có các tr ng h p sauườ ợ :
+TH1 : 0 ≤ a ≤ 1
Ta có : x2 = a(1-a) ≥ 0 => 0 ≤ x2 ≤ x1≤ 1
Suy ra 0 ≤ xn ≤ 1, nN*
Do đó : dãy (xn) không tăng, b ch n d i b i s 0ị ặ ướ ở ố
nên t n t i limxồ ạ n = b, v i b ớ [0; 1]
Chuy n qua gi i h n ta đc b = b (1 – b) ể ớ ạ ượ b = 0
V y limxận = 0 khi 0 ≤ a ≤ 1
+TH2 : a < 0 ho c a > 1ặ
Ta có: x2 < 0 => x3 < 0. T ng t ta có xươ ự n < 0, nN*, n ≥ 2
N u (xến) b ch n d i thì limxị ặ ướ n = b, v i b < 0.ớ
Chuy n qua gi i h n ta đc b = b( 1 – b) ể ớ ạ ượ b = 0 (Vô lý vì b < 0 )
V y a < 0 ho c a > 1 thì limxậ ặ n = - ∞.
Tóm l i: 0 ≤ a ≤ 1 là giá tr c n tìm.ạ ị ầ
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
3 4.0
a2.0
- D th y s (2112012)ễ ấ ố 2011 là b i s c a 9 ộ ố ủ 0.25
- S (2011)ố2012 =(9.223+4)2012 4≡2012 (mod 9)
Vì 43k+r 4≡r (mod 9) nên 42012 4≡2 7 (mod 9)≡
Suy ra : (2011)2012 7 (mod 9)≡
- S 2012 5 (mod 9)≡ố
Do đó: s A 3 (mod 9)≡ố
Suy ra: A = 9k + 3, kN => A = 3(3k + 1), kN
- Gi s A là s chính ph ng => T n t i s t nhiên x sao cho xả ử ố ươ ồ ạ ố ự 2 = A
=> x2 = 3(3k + 1) => x2
M
3 => x
M
3
=> x = 3m, v i m là s t nhiên => xớ ố ự 2 = 9m2
=> x2
M
9
=> A
M
9 (vô lí vì A = 9k + 3)
0.25
0.25
0.25
0.25
0.25
0.25
0.25
b2.0
S p x p 30 s c a t p h p A thành m t hàng theo th t tăng d n b t đu t 1.ắ ế ố ủ ậ ợ ộ ứ ự ầ ắ ầ ừ
G i 6 s đc ch n là aọ ố ượ ọ 1, a2, a3, a4, a5, a6 v i aớ1< a2< a3< a4< a5< a6
G i xọ1 là s các s đng tr c aố ố ứ ướ 1 (các s này không đc ch n)ố ượ ọ
G i xọ2 là s các s không đc ch n gi a 2 s aố ố ượ ọ ữ ố 1 và a2
G i xọ3 là s các s không đc ch n gi a 2 s aố ố ượ ọ ữ ố 2 và a3
G i xọ4 là s các s không đc ch n gi a 2 s aố ố ượ ọ ữ ố 3 và a4
G i xọ5 là s các s không đc ch n gi a 2 s aố ố ượ ọ ữ ố 4 và a5
G i xọ6 là s các s không đc ch n gi a 2 s aố ố ượ ọ ữ ố 5 và a6
G i xọ7 là s các s không đc ch n đng sau aố ố ượ ọ ứ 6
Ta có h : ệ
1 2 3 7
1 2 3 6 7
... 30 6
0, 2, 2,..., 2, 0
x x x x
x x x x x
+ + + + = −
Đt yặ2=x2 –2, y3= x3 –2, …, y6 = x6 – 2, y1 = x1, y7 = x7
Lúc này ta có hệ :
1 2 2 7
... 24 10
0, 1,2,...,7
i
y y y y
y i
+ + + + = −
=
(*)
S cách ch n 6 s th a mãn ycbt là s nghi m nguyên c a h (*)ố ọ ố ỏ ố ệ ủ ệ
M t l i gi i cho h (*) b ng vi c cài đt trên tr c s nh sauộ ờ ả ệ ằ ệ ặ ụ ố ư :
Đt tặi = yi + 1 v i i = 1, 2, 3, ...,7. Lúc đó h (*) tr thành:ớ ệ ở
(**)
Xét 1 đo n th ng AB có đ dài 21 đn v (nh hình v trên)ạ ẳ ộ ơ ị ư ẽ
V i s nguyên d ng tớ ố ươ 1, ta ch n đi m Mọ ể 1 trên đo n th ng AB sao cho AMạ ẳ 1=t1
đn vơ ị
Vì t1 ≥ 1 nên M1 ≠ A
T ng t v i s nguyên d ng tươ ự ớ ố ươ 2 , ta ch n đi m Mọ ể 2 trên đo n th ng Mạ ẳ 1B v iớ
M2≠M1 sao cho M1M2 = t2 đn v .ơ ị
Trên đo n th ng Mạ ẳ 2B ta ch n Mọ3 sao cho M2M3 = t3 đn v .ơ ị
…
Trên đo n th ng Mạ ẳ 5B ta ch n Mọ6 sao cho M6 ≠ M5 và M6 ≠ B. Suy ra: M6B = t7.
V y đ có các s tậ ể ố i ≥ 1, i=1,2,…,7 th a mãn (**) ta c n ch n ra 6 đi m Mỏ ầ ọ ể 1, M2,
…, M6 t 20 đi m trên đo n th ng AB (Hai đi m li n k có kho ng cách 1 đnừ ể ạ ẳ ể ề ề ả ơ
v )ị
0.25
0.5
0.25
0.25
0.25
2
M6
M5
M3
M2
M1
21
0
A
B
1
3
20
19
4
5
8
6
4
2
-2
-4
-6
-8
-15 -10 -5
5
10 15
N
E
M
D
A
B
C
F
S cách ch n 6 đi m t 20 đi m trên là ố ọ ể ừ ể
6
20
C
.
M i cách ch n nh v y t ng ng 1 – 1 v i 1 nghi m (tỗ ọ ư ậ ươ ứ ớ ệ 1, t2, …, t7) c a h (**).ủ ệ
V y s cách ch n 6 s th a mãn YCBT là ậ ố ọ ố ỏ
6
20
C
0.5
4 5.0
a3.0
+Ta có: AB=5, AC = 2
13
, BC = 9.
+C/m góc B, C nh n => Dọ[BC]
+ Đt x = BD, y = DC, ta có h :ặ ệ
2 2
9
27
x y
y x
+ =
− =
x= 3 và y = 6
Suy ra : BD= 3, DC = 6, DA = 4
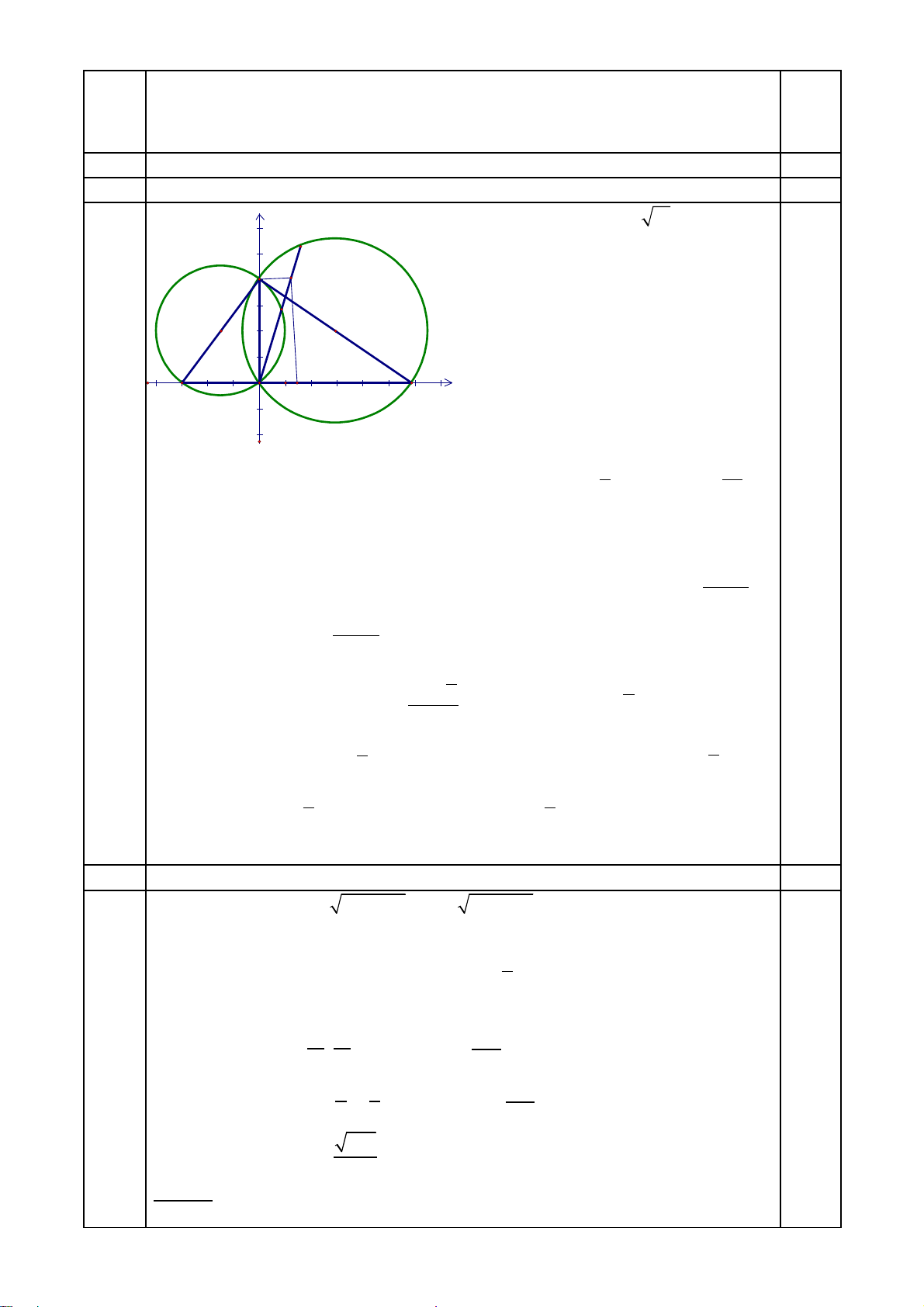
+ Ch n h t a đ trong m t ph ng saoọ ệ ọ ộ ặ ẳ
cho D(0; 0), B( - 3; 0), A( 0; 4).
Suy ra: C( 6; 0).
+ Ta có ph ng trình các đng trònươ ườ
đng kính AB và đng kính AC l n l t là : ườ ườ ầ ượ
( )
22
3 25
2
2 4
x y
� �
+ + − =
� �
� �
và
( ) ( )
2 2
3 2 13x y− + − =
+ Đng th ng (∆) đi qua D không trùng v i DA có ph ng trình y = kx.ườ ẳ ớ ươ
E là giao đi m c a (∆) và đng tròn đng kính AB, E≠ A nên ể ủ ườ ườ
2
4 3
1
E
k
xk
−
=+
T ng t , ta có ươ ự
2
4 6
1
F
k
xk
+
=+
Suy ra hoành đ đi m N là a = ộ ể
2
3
42
1
k
k
+
+
hay
( )
2
3
1 4 2
k a k+ = +
+ T N(a; ka), A(0; 4), M(ừ
3
2
;0). Suy ra:
( )
; 4AN a ka= −
uuuur
và
3;
2
MN a ka
� �
= −
� �
� �
uuuur
=>
( )
2 2 2 2
3 3
. 4 1 4
2 2
AN MN a a k a ka a k a k
� �
= − + − = + − −
� �
� �
uuuur uuuur
=0
V y AN vuông góc v i MN (đpcm)ậ ớ
0.25
0.25
0.25
0.5
0.25
0.25
0.25
0.25
0.25
0.25
0.25
b2.0
Ta có : AN2 + NM2 ≥
2 .AN NM
hay
2 .AN NM
≤ AM2 (S không đi)ố ổ
Suy ra: Di n tích tam giác AMN đt GTLN khi AN = NMệ ạ
Lúc đó: AN2 = NM2
( ) ( )
2
2 2
2
3
42
a ka a ka
� �
+ − = − +
� �
� �
k2 = 1
V i k = 1, ta có: Nớ
11 11
;
4 4
� �
� �
� �
, suy ra CN2 =
290
16
V i k = -1, ta cóớ : N
5 5
;
4 4
� �
− −
� �
� �
, suy ra CN2 =
576
16
V y GTNN c a CN là ậ ủ
290
4
L u ýư : Không tính đi m cho Hình v câu này; Hình v là c s đ thuy t minhể ẽ ẽ ơ ở ể ế
l i gi i mà thôi. ờ ả
0.5
0.25
0.25
0.25
0.25
0.25
0.25
3
5
( ) ( )
( )
( )
2
f xf x +f y = f x +y, x,y R
∀
� �
� �
(*) 3.0
+Ch ng minh f là song ánh.ứ
- C/m f đn ánhơ :
y1, y2R, ta có : f(y1) = f(y2) => f[xf(x) +f(y1)] = f[xf(x) +f(y2)]
=> [f(x)]2 + y1 = [f(x)]2 + y2 => y1 = y2 => f là đn ánh (đpcm) ơ(1)
- C/m f toàn ánh :
VP(*) là hàm s b c nh t theo y, khi c đnh x => VT(*) có mi n giá tr R.ố ậ ấ ố ị ề ị
Suy ra f toàn ánh (đpcm) (2)
(1) & (2), suy ra f song ánh (đpcm)
Do đó t n t i duy nh t s th c a sao cho f(a) = 0.ồ ạ ấ ố ự
+ Xét x = 0 và x =a, thay vào (*), ta đc :ượ
( )
( )
( )
( )
( )
2
0f f y f y
f f y y
= +� �
� �
=
=> f(0) = 0
Lúc này, ta có: f(0) = 0 và f(f(y)) = y, yR
+Xét y = 0, thay vào (*) : f(xf(x) + f(0)) = [f(x)]2 , v i ớxR
=> f(xf(x)) = [f(x)]2 , xR (3)
=> f [f(x).f(f(x))] = [f(f(x))]2 , xR
=> f(f(x).x) = x2 , xR (4)
T (3) và (4), suy ra: [f(x)]ừ2 = x2 ,xR
=> f(x) = x ho c f(x) = - x , v i ặ ớ xR
+ Ta ch ng minh không t n t i 2 s a, b≠ 0 sao cho không đng th i x y ra ứ ồ ạ ố ồ ờ ả
f(a) = a và f(b) = -b.
Th t v y, thay vào (*), ta đc: f(bậ ậ ượ 2 – b) = a2 + b
=> (a2 – b)2 = (a2 + b)2 => 4a2b = 0 => a = 0 ho c b = 0 (mâu thu n a, b ≠ 0)ặ ẩ
Do đó: f(x) = x, xR ho c f(x) = - x , ặxR
+ Th l i:ử ạ
. f(x) = x, xR, thay vào (*): f(x2 + x) = x2 + x x2 + x = x2 + x (đúng)
. f(x) = - x, xR, thay vào (*): f(- x2 - x) = (- x)2 + x
-(-x2 – x) = x2 + x (đúng)
Tóm l i: hàm s f c n tìm là f(x) = x , ạ ố ầ xR ho c f(x) = - x , ặxR
0.25
0.25
0.25
0.25
0.5
0.25
0.25
0.25
0.25
0.25
0.25
6 2.5
Không m t tính t ng quát, đt z =min{x, y, z}ấ ổ ặ
Ta có : x ≥ x – z > 0, y ≥ y – z > 0
Suy ra : A ≥
( )
( )
2 2
22 2
1 1 1
x y x y
x y
� �
+ + +
� �
−
� �
� �
Đt M ặ=
( )
( )
2 2
22 2
1 1 1
x y x y
x y
� �
+ + +
� �
−
� �
� �
=
( ) ( )
2 2
2
22 2
1
2x y
x y xy x y
x y
� �
+
� �
− + +
� �
� � −
� �
� �
=
( ) ( ) ( )
2
2
22 2
2
1
2x y xy
x y xy x y
x y
� �
− +
� �
− + +
� �
� � −
� �
� �
=
( ) ( )
2
2
2
2
2
1x y xy
xy
xy
x y
� �
− +
+ +� �
−� �
� �
0.25
0.5
4
=
( ) ( )
2
2
2
2
1 2
x y
xy
xy
x y
� �
−
+ + +
� �
−� �
� �
Đt t = ặ
( )
2
0
x y
xy
−>
. Ta có : M = f(t) = 1 +
( )
2
2+ t+2
t
Hay ta có: f(t) =
2
2
t +4t+ +5
t
, Df = (0; +∞ )
f ’(t) =
( )
( )
2
3 2
2 2 2
2 t+1 t +t-1
2 2t +4t -2
2t+4- = =
t t t
f ’(t) = 0 , t Df t =
5 1
2
−
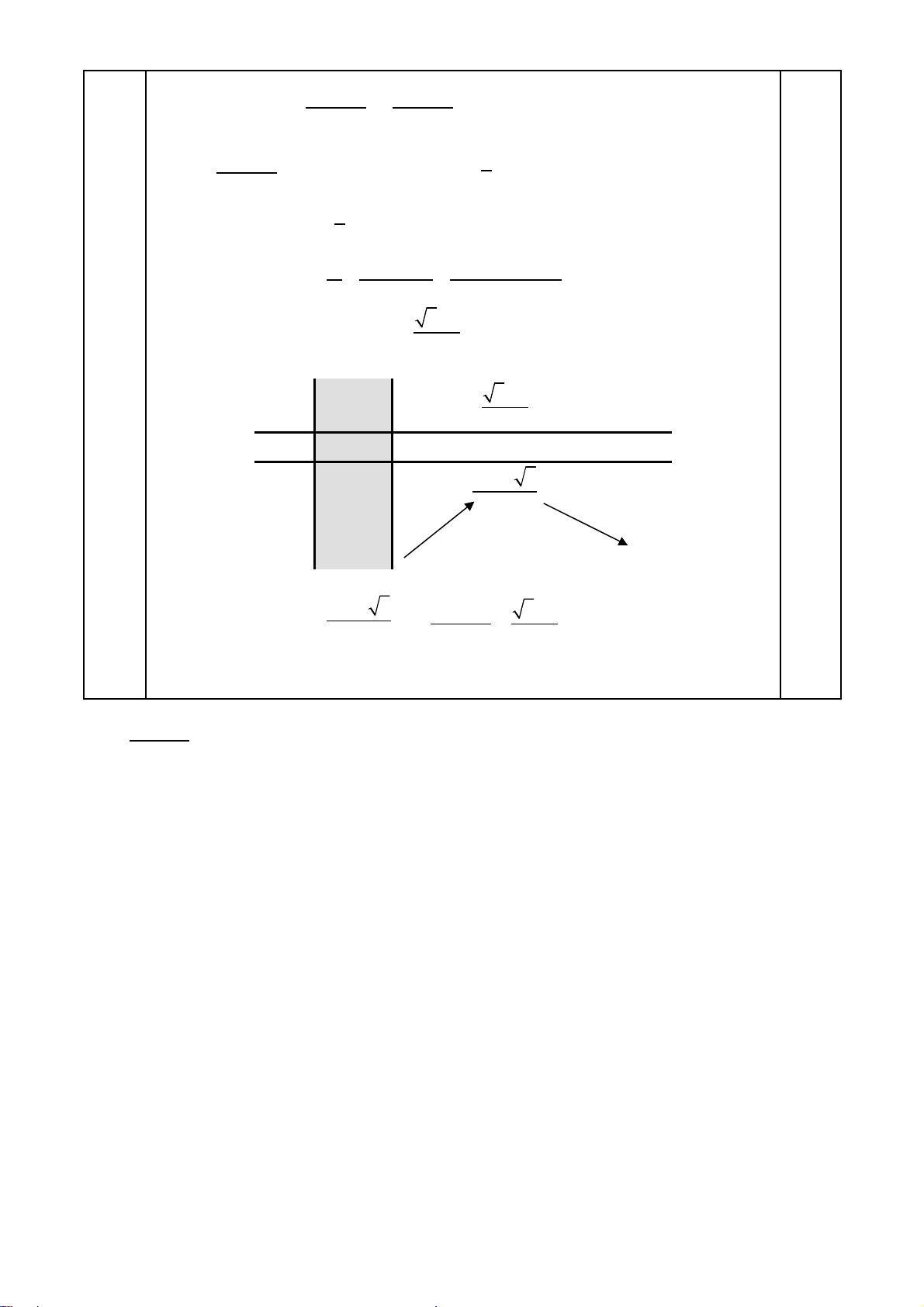
B ng bi n thiênả ế :
t
5 1
2
−
+∞
f’(t) - 0 +
f(t)
11 5 5
2
+
Suy ra :
( )
11 5 5
2
Min
f
D
f t +
=
khi
( )
2
5 1
2
x y
xy
−−
=
và z = 0
0.5
0.25
0.25
0.25
0.25
0.25
Ghi chú: N u thí sinh có cách gi i khác nh ng v n đúng thì ban giám kh o c n th o lu nế ả ư ẫ ả ầ ả ậ
th ng nh t bi u đi m và cho đi m phù h p v i thang đi m.ố ấ ể ể ể ợ ớ ể
=============
5
0