SỞGD&ĐTVĨNHPHÚCKỲKSCLTHIĐẠIHỌCNĂMHỌC20122013 LẦN1
ĐỀTHIMÔN:TOÁN KHỐIA,A1
Thờigianlàmbài:180phút,khôngkểthờigiangiaođề
I.PHẦNCHUNGCHOTẤTCẢTHÍSINH (7,0 điểm)
Câu 1(2,0điểm)Chohàmsố 3 2
2
x
y x
-
= -,cóđồthịlà ( )C .
a)Khảosátsựbiếnthiênvàvẽđồthị (C)củahàmsố đãcho.
b)Viếtphươngtrìnhtiếptuyếndcủađồthị(C),biếttiếptuyến dtạovớitrụcOxmộtgóc
a
sao
cho 1
cos 17
a
=.
Câu 2(1,0điểm)Giảiphươngtrình: sin 2 cos 2 5sin cos 3 0
2cos 3
x x x x
x
+ + - - =
-.
Câu 3(1,0điểm)Giảihệphươngtrình: 2 2
( )( 5) 8
( 1) 3
x y xy y
x y x y
+ + + = -
ì
í + + + =
î
Câu4(1,0điểm)Tìmtấtcảcácgiátrịcủamđểphươngtrình: 3 1mx x m - - = + cóhainghiệm
thựcphânbiệt.
Câu5(1,0điểm)ChohìnhchópS.ABCDcóđáy ABCDlàhìnhvuôngcạnha.Hìnhchiếuvuông
góc của S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABD. Cạnh SD tạo với đáy
(ABCD)mộtgócbằng 60
o.TínhthểtíchkhốichópS.ABCDvàkhoảngcáchtừAtớimặtphẳng
(SBC)theo a.
Câu 6(1,0điểm)Tìmtấtcảcácgiátrịthựccủa mđểvớimọi xthuộc 0;2
p
æ ö
ç ÷
è øtađềucó
8 8 2
tan cot 64cos 2x x m x + ³ +.
II.PHẦNRIÊNG(3,0 điểm)Thísinhchỉđượclàmmộttronghaiphần(phầnAhoặc phầnB)
A.TheochươngtrìnhChuẩn
Câu 7.a (1,0 điểm) Chođường tròn 2 2
( ) : 4 6 12 0C x y x y + - + - =và điểm (2; 4 3)M. Viết
phươngtrình đườngthẳng dcắtđườngtròn (C)tạihaiđiểm A,BsaochotamgiácMABđều.
Câu 8.a (1,0 điểm)Tìmhệsốcủa 4
x trongkhaitriểnthànhđathứccủabiểuthức: 2 10
(1 4 )x x + + .
Câu 9.a (1,0 điểm)Giảiphươngtrình:
( ) ( )
2
2 2 2
2 2 4
2
3 7 3 7 2
x x
x x x x +
+ + +
+ + - =.
B.TheochươngtrìnhNângcao
Câu7.b(1,0điểm)Choelíp
2 2
( ) : 1
9 4
x y
E + = vàđiểm (1; 1)I .Viếtphươngtrìnhđườngthẳngd
qua Icắt(E)tạihaiđiểmM,NsaochoIlàtrungđiểmcủa MN.
Câu 8.b(1,0điểm)Tínhgiớihạn:
3
1
2 1 3 2
lim 1
x
x x
x
®
- - -
-.
Câu9.b (1,0 điểm)Cótấtcả baonhiêusốtựnhiêncó5chữsốkhácnhaumàtrongmỗisốđó
luôncómặthai chữsốlẻvàbachữsốchẵn.
Hết
Cảm ơnthầyNguyễnDuyLiên(lientoancvp@vinhphuc.edu.vn)đãgửitới
www.laisac.page.tl
SỞGD&ĐTVĨNHPHÚCKỲKSCLTHIĐẠIHỌCNĂMHỌC20122013
HƯỚNGDẪNCHẤMMÔN:TOÁN KHỐIA,A1
———————————
I.LƯUÝCHUNG:
Hướngdẫnchấmchỉtrìnhbàymộtcáchgiảivớinhữngýcơbảnphảicó.Khichấmbàihọcsinh
làmtheocáchkhácnếuđúngvàđủýthìvẫnchođiểmtốiđa.
Điểmtoànbàitínhđến0,25vàkhônglàmtròn.
Vớibàihìnhhọcnếuthísinhkhôngvẽhìnhphầnnàothìkhôngchođiểmtương ứngvới phầnđó.
II.ĐÁPÁN:
Câu Ý Nộidungtrìnhbày Điểm
1 a 1,0điểm
TXĐ: \{2}.D =¡
Giớihạn,tiệmcận:
4
lim lim 3 3
2
x x
y x
®+¥ ®+¥
æ ö
= + =
ç ÷
-
è ø; 4
lim lim 3 3
2
x x
y x
®-¥ ®-¥
æ ö
= + =
ç ÷
-
è ø
2 2
4
lim lim 3 2
x x
y x
+ +
® ®
æ ö
= + = +¥
ç ÷
-
è ø; 2 2
4
lim lim 3 2
x x
y x
- -
® ®
æ ö
= + = -¥
ç ÷
-
è ø
ĐồthịcóTCĐ: 2x =;TCN: 3y = .
0.25
Sựbiếnthiên: 2
4
' 0 2
( 2)
y x
x
= - < " ¹
-,suyrahàmsốnghịchbiếntrêncáckhoảng
( ;2) & (2; ) -¥ +¥
0.25
BBT
x -¥2 +¥
y’ - -
y
3 +¥
-¥3
0.25
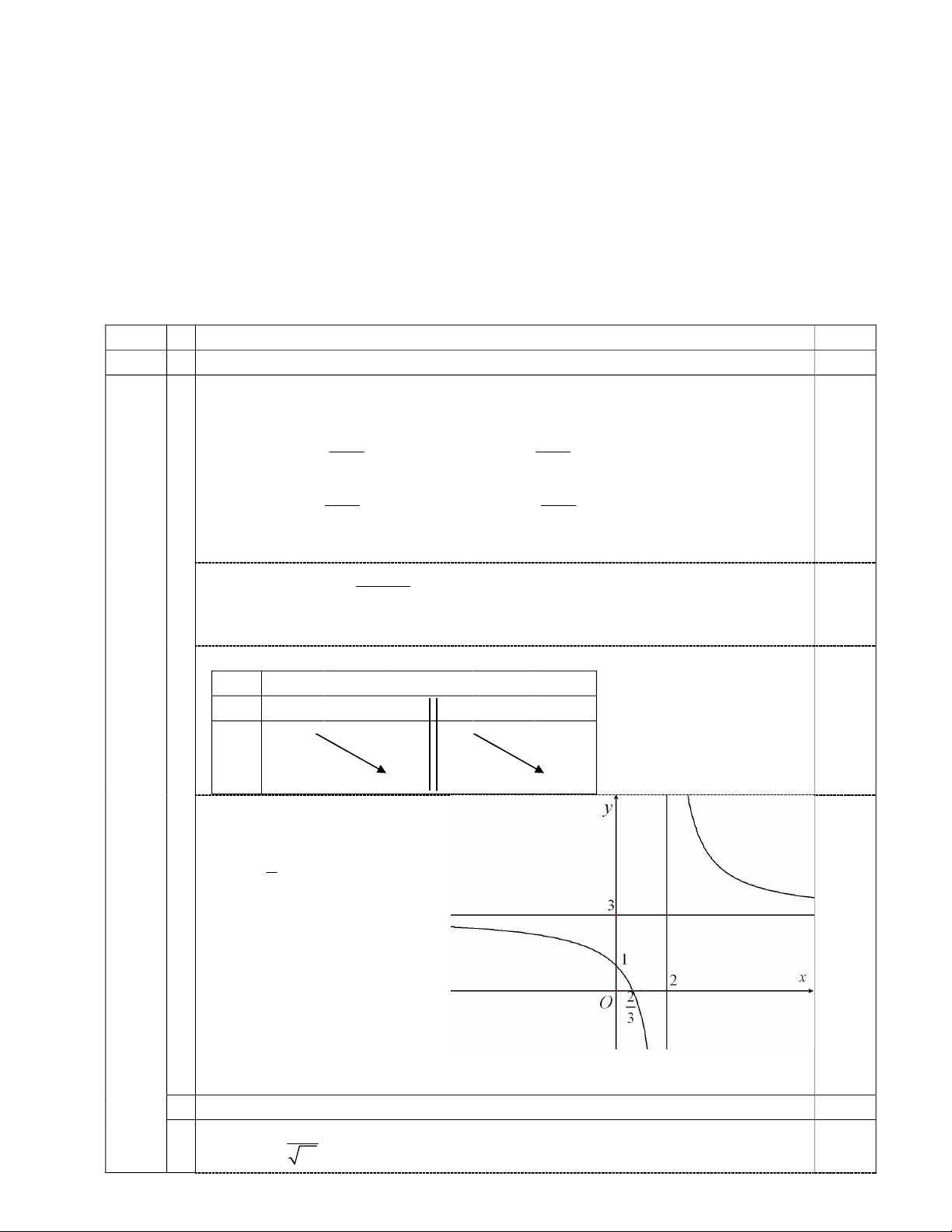
Đồthị:
GiaovớiOytại: (0; 1) ,giaovới
Oxtại: 2; 0
3
æ ö
ç ÷
è ø
Đồ thị nhận giao điểm của hai
tiệmcậnlàmtâmđốixứng. 0.25
b 1,0điểm
Do 1
cos tan 4
17
= Þ = ±
a a
. 0.5
Vì '( ) 0, 2y x x < " ¹suyrahệsốgóccủa dbằng 4 - .
Giả sử d tiếp xúc với (C) tại điểm 0 0 0
( ; ), 2.M x y x ¹
0
0 2
00
1
4
'( ) 4 3.
( 2)
x
y x x
x
=
é
= - = - Û ê =
- ëVới 0 0
1 1x y = Þ = - ;với 0 0
3 7x y = Þ =0.25
Vậycóhaiphươngtrìnhtiếptuyến dthỏamãnlà: 4 3y x = - + và 4 19y x = - + . 0.25
2 1,0điểm
sin 2 cos 2 5sin cos 3 0 (1)
2cos 3
x x x x
x
+ + - - =
-Đk: 3
cos 2 , .
2 6
x x k k ¹ Û ¹ ± + ΢
p p
0.25
(1) sin 2 cos2 5sin cos 3 0x x x x Û + + - - =
2
cos (2sin 1) (2sin 5sin 2) 0x x x x Û - - - + =0.25
(2sin 1)(cos sin 2) 0x x x Û - - + =
2
1 6
sin 52 2
6
x k
x
x k
é = +
ê
Û = Û ê
ê = +
ê
ë
p p
p p
0.25
Kếthợpđiềukiệnsuyraphươngtrìnhcónghiệm 5 2 ( )
6
x k k
p p
= + ΢. 0.25
3 1,0điểm
2
2
( ) ( )( 5) 8
( ) ( ) ( ) 3
x y x y xy x
I x y xy x
ì + + + - + = -
ï
Û í + - - =
ï
î0.25
Đặtx y a
xy x b
+ =
ì Þ
í - =
îhệ(I)códạng:
2
2
( 5) 8
3
a a b
a b
ì + + = -
ï
í - =
ï
î
2 2
( 2) 8a a a Þ + + = -
3 2 2 8 0a a a Û + + + =2
( 2)( 4) 0 2 1a a a a b Û + - + = Û = - Þ =
0.25
Với 2
2
2 2
1 1 3 1 0
x y
a x y
b xy x x x
+ = -
= - + = - ì
ì ì
Û Û
í í í
= - = + + =
î î î
3 5
2
1 5
2
3 5
2
1 5
2
x
y
x
y
éì - +
=
êï
ï
ê
í
ê - -
ï =
ê
ï
î
ê
Û ê
ì - -
ê =
ï
ï
ê
í
ê - +
ï
ê =
ï
êî
ë
0.25
Vậyhệphươngtrìnhcónghiệm 3 5 1 5 3 5 1 5
; ; ;
2 2 2 2
æ ö æ ö
- + - - - - - +
ç ÷ ç ÷
ç ÷ ç ÷
è ø è ø
. 0.25
4 1,0điểm
Đk: 3x ³
Pttươngđương
( )
3 1
1 3 1 1
x
m x x m x
- +
- = - + Û = -
0.25
Đặt 3 1
( ) 1
x
f x x
- +
= -với 3x ³
Khiđó: 2
5 2 3
'( ) 0
2 3( 1)
x x
f x x x
- - -
= =
- -2
5 2 3 0 7 2 3
2 3( 1)
x x x
x x
- - -
Û = Û = -
- -
0.25
![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)
![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)
