
Câu I: (2,0 điểm) Cho hàm số y =
1
x
x
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm tọa độ điểm M thuộc (C), biết rằng tiếp tuyến của (C) tại M vuông góc với
đường thẳng đi qua điểm M và điểm I(1; 1).
Câu II: (2,0 điểm)
1. Giải phương trình:
3 2
cos cos
2 1 sin .
sin cos
x x
x
x x
2. Giải hệ phương trình:
2
2 2
( ) 4 1
( ) 2 7 2
x x y y x
x x y y x
Câu III: (1,0 điểm) Tính tích phân:
1
ln
1 ln
ex
dx
x x
Câu IV: (1,0 điểm) Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân đỉnh C;
đường thẳng BC’ tạo với mặt phẳng (ABB’A’) góc
0
60
và AB = AA’ = a. Gọi M, N, P lần
lượt là trung điểm của BB’, CC’, BC và Q là một điểm trên cạnh AB sao cho BQ =
4
a
.
Tính theo a thể tích khối lăng trụ ABC.A’B’C’ và chứng minh rằng
(MAC) (NPQ)
.
Câu V: (1,0 điểm) Chứng minh rằng với mọi số thực không âm a, b, c thỏa mãn điều kiện
3
ab bc ca
, ta có: 2 2 2
1 1 1
1
2 2 2
abc
Câu VI: (2,0 điểm)
1. Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có tâm I(2;1) và AC = 2BD.
Điểm M
1
(0; )
3
thuộc đường thẳng AB, điểm N(0;7) thuộc đường thẳng CD. Tìm tọa độ đỉnh B
biết B có hoành độ dương.
2.Trong không gian với hệ tọa độ Oxyz, cho ba đường thẳng :
1: 4
1 2
x t
d y t
z t
; d2: 2
1 3 3
x y z
và d3:
1 1 1
5 2 1
x y z
. Viết phương trình đường
thẳng , biết cắt ba đường thẳng d1 , d2 , d3 lần lượt tại các điểm A, B, C sao cho AB = BC.
Câu VII: (1,0 điểm) Tìm số phức z thỏa mãn : 2
2
2 . 8
z z z z
và
2
z z
------------------------Hết----------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm
Họ và tên:………………………………………………..SBD:………………
www.laisac.page.tl
TRƯỜNG THPT
CHUYÊN
NGUY
ỄN HUỆ
KỲ THI THỬ ĐẠI HỌC LẦN THỨ HAI NĂM HỌC 2010 – 2011
ĐỀ THI MÔN: TOÁN KHỐI A
Th
ời gian l
àm bài: 180 phút, không k
ể thời gian giao đề
TRƯỜNG THPT
CHUYÊN
NGUYỄN HUỆ
HƯỚNG DẪN CHẤM THI THỬ ĐẠI HỌC LẦN THỨ HAI
NĂM HỌC 2010 – 2011
ĐỀ THI MÔN: TOÁN
CÂU NỘI DUNG ĐIỂM
TXĐ : D = R\{1}
y’ = 2
1
0
( 1)x
0,25
lim ( ) lim ( ) 1
x x
f x f x
nên y = 1 là tiệm cận ngang của đồ thị hàm số
1 1
lim ( ) ,lim
x x
f x
nên x = 1 là tiệm cận đứng của đồ thị hàm số
0,25
Bảng biến thiên
1
+
-
1
- -
y
y'
x- 1 +
Hàm số nghịch biến trên
( ;1)
và
(1; )
Hàm số không có cực trị
0,25
I-1
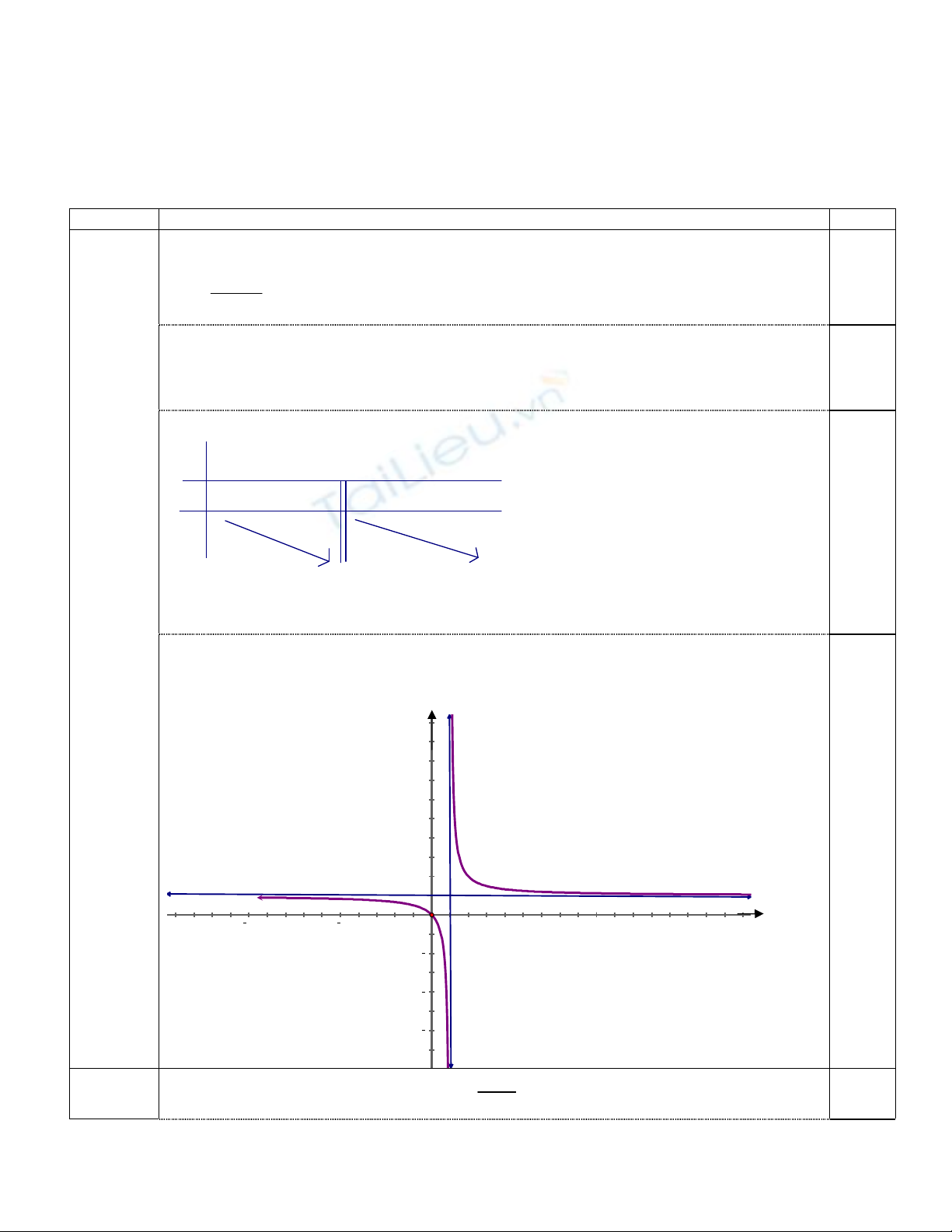
(1 điểm) Đồ thị :
Nhận xét : Đồ thị nhận giao điểm của 2 đường tiệm cận I(1 ;1) làm tâm đối xứng
10
8
6
4
2
2
4
6
8
10 5 5 10 15
0,25
I-2
(1 điểm) Với 0
1
x
, tiếp tuyến (d) với (C) tại M(x0 ; 0
0
1
x
x
) có phương trình : 0,25

0
0
2
0 0
1( )
( 1) 1
x
y x x
x x
2
0
2 2
0 0
1
0
( 1) ( 1)
x
x y
x x
(d) có vec – tơ chỉ phương
2
0
1
( 1; )
( 1)
ux
r
0
0
1
( 1; )
1
IM x x
uuur
0,25
Để (d) vuông góc IM điều kiện là :
0
020
0 0
0
1 1
. 0 1.( 1) 0
2
( 1) 1
x
u IM x x
x x
r uuur 0,25
+ Với x0 = 0 ta có M(0,0)
+ Với x0 = 2 ta có M(2, 2) 0,25
ĐK:
sin cos 0
x x
0,25
Khi đó
2
1 sin cos 1 2 1 sin sin cos
PT x x x x x
1 sin 1 cos sin sin .cos 0
x x x x x
1 sin 1 cos 1 sin 0
x x x
0,25
sin 1
cos 1
x
x
(thoả mãn điều kiện) 0,25
II-1
(1 điểm)
2
2
2
x k
x m
,k m
Z
Vậy phương trình đã cho có nghiệm là:
2
2
x k
và
2
x m
,k m
Z
0,25
Với x = 0 không nghiệm đúng phương trình
Với
0
x
, ta có:
2
2 2
2 2 2
2
1
4
1 4
( ) 2 2 7 1
( ) 2 7
yx y
x y xy x x
x x y y x y
x y x
0,25
Đặt
21,
y
u v x y
x
ta có hệ: 2 2
4 4 3, 1
2 7 2 15 0 5, 9
u v u v v u
v u v v v u
0,25
+) Với
3, 1
v u
ta có hệ:
2 2 2
1, 2
1 1 2 0
2, 5
3 3 3
y x
y x y x y y
y x
x y x y x y
.
0,25
II-2
(1 điểm)
+) Với
5, 9
v u
ta có hệ:
2
1 9
5
y x
x y
, hệ này vô nghiệm.
Vậy hệ đã cho có hai nghiệm:
( ; ) (2;1), ( ; ) (5; 2).
x y x y
0,25
III
(1 điểm)
Đặt t =
1 ln
x
có 2tdt =
1
dx
x
x = 1 thì t = 1; x = e thì t =
2
0,25
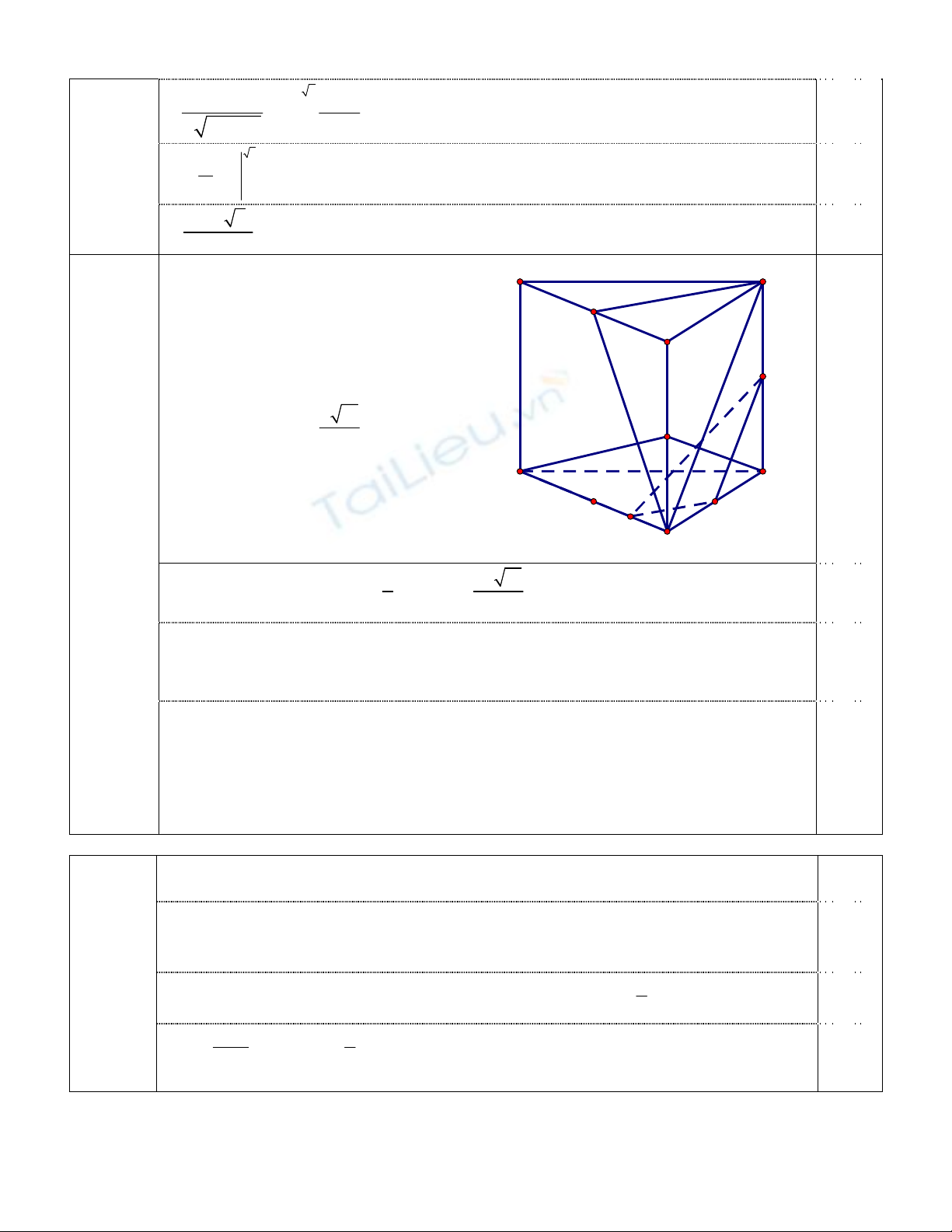
22
1 1
ln 12
1 ln
ex t
dx tdt
t
x x
0,25
2
3
1
2( )
3
tt
0,25
2(2 2)
3
0,25
Gọi I là trung điểm A’B’ thì
' ' '
' ( ' ')
' AA'
C I A B
C I ABA B
C I
suy ra góc giữa BC’ và mp(ABB’A’) chính
là góc
·
'
C BI
.
Suy ra
·
0
' 60
C BI
·
15
' .tan '
2
a
C I BI C BI
Q
P
K
M
I
N
C
A
B
A'
C'
B'
0,25
3
. ' ' ' ' ' '
1 . 15
. .
AA'. AA' . ' '
2 4
ABC A B C A B C
a
V S CI A B 0,25
/ / '
( ) / /( ' )
/ / '
NP BC
NPQ C BI
PQ C I
(1) 0,25
IV
(1 điểm)
·
·
· ·
0
' ( ) '
' 90 AM BI
ABM BB I c g c suy ra AMB BIB
suy ra AMB B BI
V V .
Mặt khác theo chứng minh trên C’I
AM nên AM
( ' )
C BI
Suy ra (AMC)
( ' )
C BI
(2)
Từ (1) và (2) suy ra
(MAC) (NPQ)
0,25
Bất đẳng thức cần chứng minh tương đương: 2 2 2 2 2 2 2 2 2
4
a b b c c a a b c
0,25
Đặt x = ab, y = bc, z = ca ta cần chứng minh 2 2 2
4
x y z xyz
với mọi x, y, z
không âm thỏa mãn: x + y + z = 3
Không làm mất tính tổng quát giả sử x
y; x
z thì x
1 ta có: 0,25
2 2 2 2 2 2 2 2
1
4 ( ) ( 2) 4 ( ) ( ) ( 2) 4
4
x y z xyz x y z yz x x y z y z x
0,25
V
(1 điểm)
2 2 2
2 1
(3 ) 4 ( 1) ( 2) 0
4 4
x
x x x x
Dấu bằng xảy ra khi a = b = c = 1 0,25
N
D
I
A
C
B
N'
M
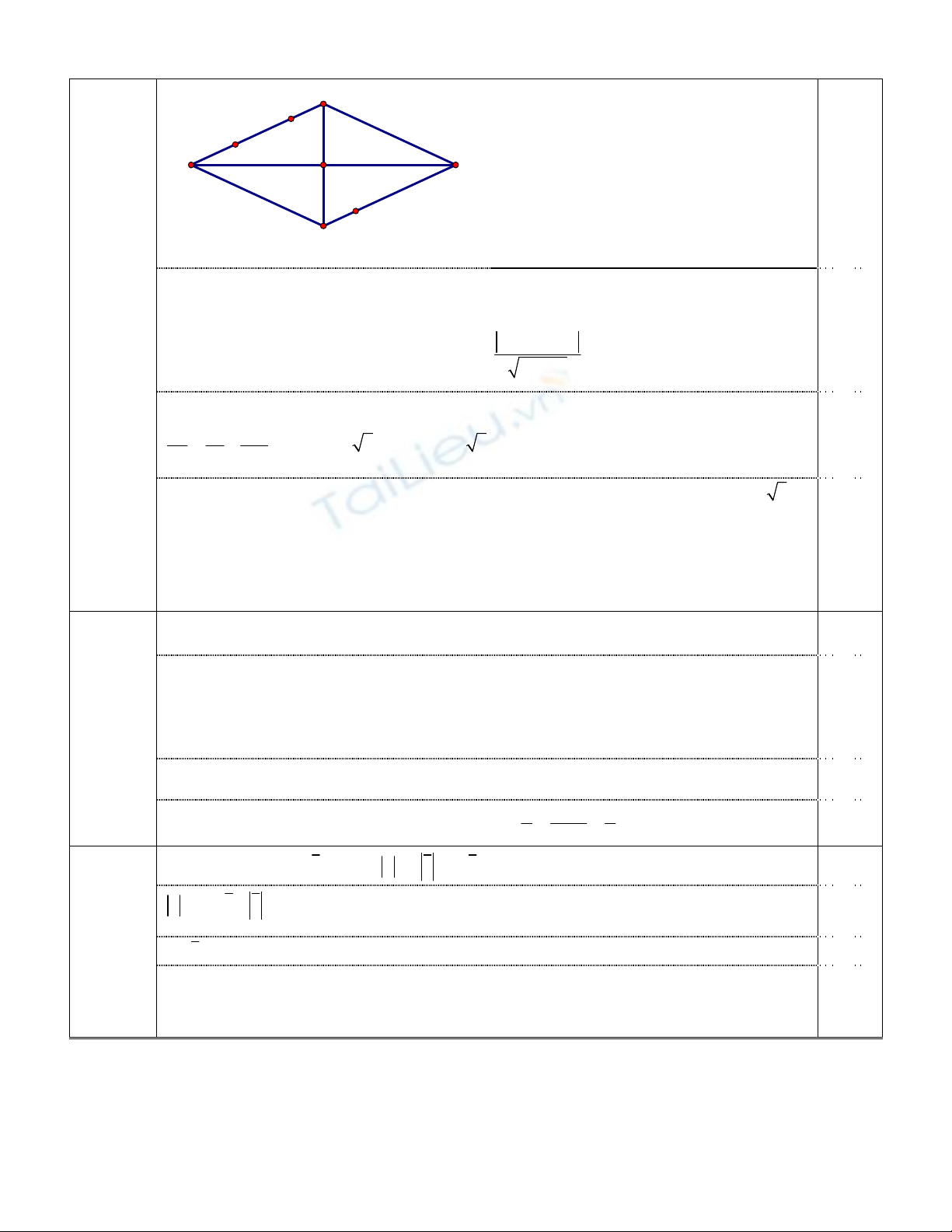
Gọi N’ là điểm đối xứng của N qua I thì N’
thuộc AB, ta có :
'
'
2 4
2 5
N I N
N I N
x x x
y y y
0,25
Phương trình đường thẳng AB:
4x + 3y – 1 = 0
Khoảng cách từ I đến đường thẳng AB: 2 2
4.2 3.1 1
2
4 3
d
0,25
AC = 2. BD nên AI = 2 BI, đặt BI = x, AI = 2x trong tam giác vuông ABI có:
2 2 2
1 1 1
4
d x x
suy ra x =
5
suy ra BI =
5
0,25
VI.-1
(1 điểm)
Điểm B là giao điểm của đường thẳng 4x + 3y – 1 = 0 với đường tròn tâm I bán kính
5
Tọa độ B là nghiệm của hệ: 2 2
4x 3y – 1 0
( 2) ( 1) 5
x y
B có hoành độ dương nên B( 1; -1)
0,25
Xét ba điểm A, B, C lần lượt nằm trên ba đường thẳng d1 , d2 , d3
Ta có A (t, 4 – t, -1 +2t) ; B (u, 2 – 3u, -3u) ; C (-1 + 5v, 1 + 2v, - 1 +v) 0,25
A, B, C thẳng hàng và AB = BC
B là trung điểm của AC
( 1 5 ) 2
4 (1 2 ) 2.(2 3 )
1 2 ( 1 ) 2( 3 )
t v u
t v u
t v u
0,25
Giải hệ trên được: t = 1; u = 0; v = 0
Suy ra A (1;3;1); B(0;2;0); C (- 1; 1; - 1) 0,25
VI -2
(1 điểm)
Đường thẳng đi qua A, B, C có phương trình 2
1 1 1
x y z
0,25
Gọi z = x + iy ta có 2
2
2 2
;
z x iy z z zz x y
0,25
2
22 2 2 2
2 . 8 4( ) 8 ( ) 2 (1)
z z z z x y x y 0,25
2 2 2 1 (2)
z z x x 0,25
VII
(1 điểm) Từ (1) và (2) tìm được x = 1 ; y =
1
Vậy các số phức cần tìm là 1 + i và 1 - i 0,25












![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)



