Bài ging môn K thut ðin t C
GV: Lê Th Kim Anh
1
Chương 5 H THNG S VÀ MÃ
I. BIU DIN S:
Mt s trong h" thng s ñư$c t&o ra t( mt hay nhi,u
ký s (digit), có th2 bao g4m 2 ph7n: ph7n nguyên và
ph7n l<, ñư$c phân cách nhau b?ng dAu chAm cơ s
(radix).
Trng s (Weight)cBa mCi ký s phF thuc vào vG trí
cBa ký s ñó.
TrIng s = Cơ s
VG trí
Bài ging môn K thut ðin t C
GV: Lê Th Kim Anh
2
Giá tr ca s ñư$c tính b?ng tKng cBa các tích ký s
vLi trIng s.
Ký s N tOn cùng bên trái ñư$c gIi là ký s có trIng
s lLn nhAt (Most Significant Digit – MSD), ký s N
tOn cùng bên phQi ñư$c gIi là ký s có trIng s nhR
nhAt (Least Significant Digit – LSD).
Giá trG = ∑
∑∑
∑Ký s. TrIng s
V trí ca ký s ñư$c ñánh thS tT t( 0 cho ký s hàng
ñơn vG, thS tT này ñư$c tăng lên 1 cho ký s bên trái
và giQm ñi 1 cho ký s bên phQi.
Bài ging môn K thut ðin t C
GV: Lê Th Kim Anh
3
H THNG S THXP PHÂN (DECIMAL ^ DEC)
H" thOp phân có cơ s là 10, s_ dFng 10 ký s là
0,1,2,3,4,5,6,7,8,9.
ð2 phân bi"t s thOp phân vLi s cBa các h" thng s
khác, ta thêm ký hi"u D (decimal) hohc 10 N d&ng chi
s dưLi vào ñ?ng sau.
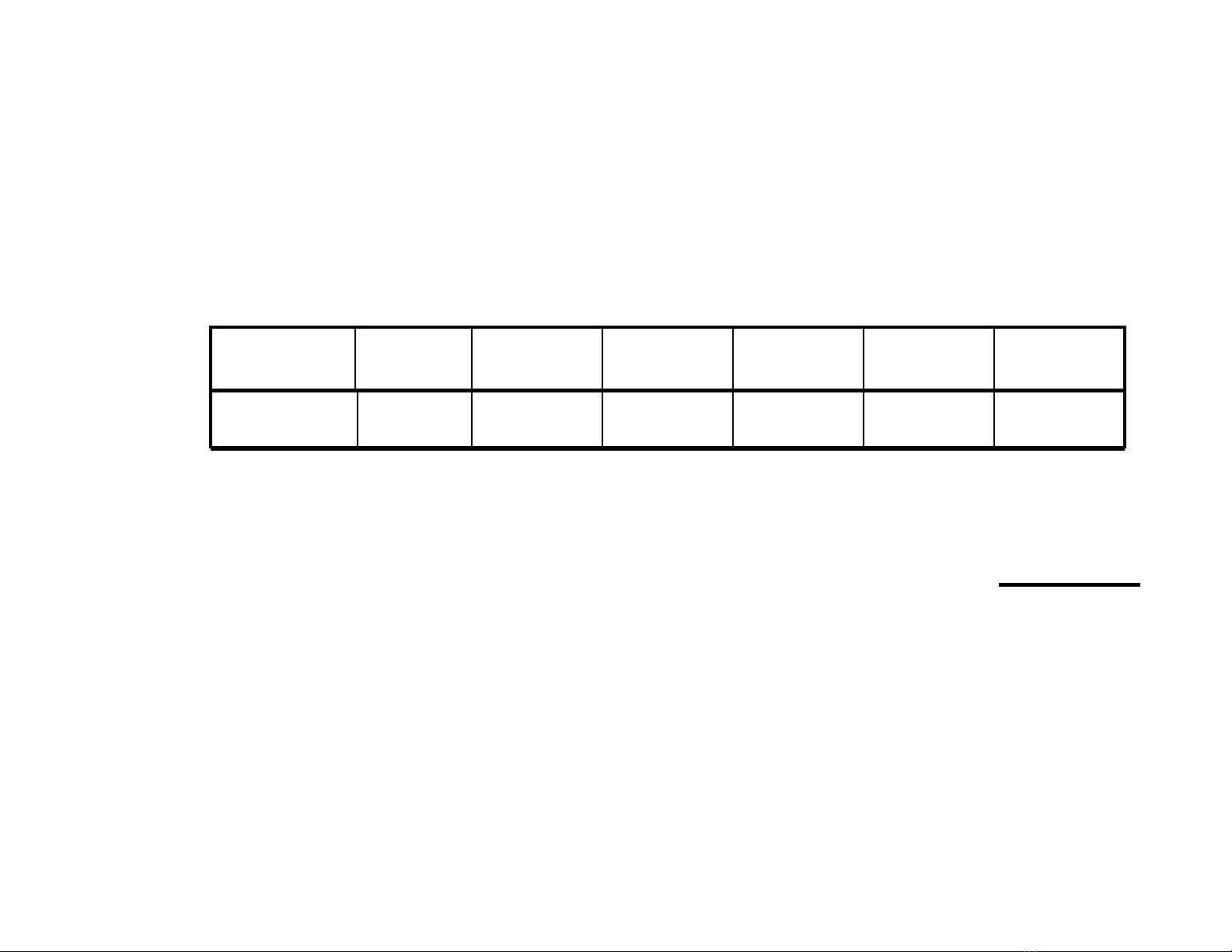
2x10
2
+ 4x10
1
+ 7x10
0
+ 6x10
^1
+2x10
^2
+ 5x10
^3
= 247.625
10
^3
10
^2
10
^1
.10
0
10
1
10
2
^3^2^1.012
Ví dF:
Giá trG :
Bài ging môn K thut ðin t C
GV: Lê Th Kim Anh
4
H THNG S NHl PHÂN (BINARY^BIN)
H" nhG phân có cơ s là 2, s_ dFng 2 ký s là 0 và 1.
Nguyên toc t&o ra s nhG phân, cách tính trIng s và
giá trG cBa s nhG phân tương tT vLi cách ñã thTc
hi"n ñi vLi s thOp phân.
S nhG phân ñư$c ký hi"u bNi ký tT B (binary) hohc
s 2 N d&ng chi s dưLi.
Bài ging môn K thut ðin t C
GV: Lê Th Kim Anh
5
Bit n?m tOn cùng bên trái ñư$c gIi là bit có trIng s
lLn nhAt (Most Significant Bit –MSB).
Bit n?m tOn cùng bên phQi ñư$c gIi là bit có trIng s
nhR nhAt (Least Significant Bit –LSB).
S nhG phân ñư$c dùng ñ2 bi2u disn các tín hi"u
trong m&ch s.
MCi ký s trong h" nhG phân ñư$c gIi là 1 bit (binary
digit).
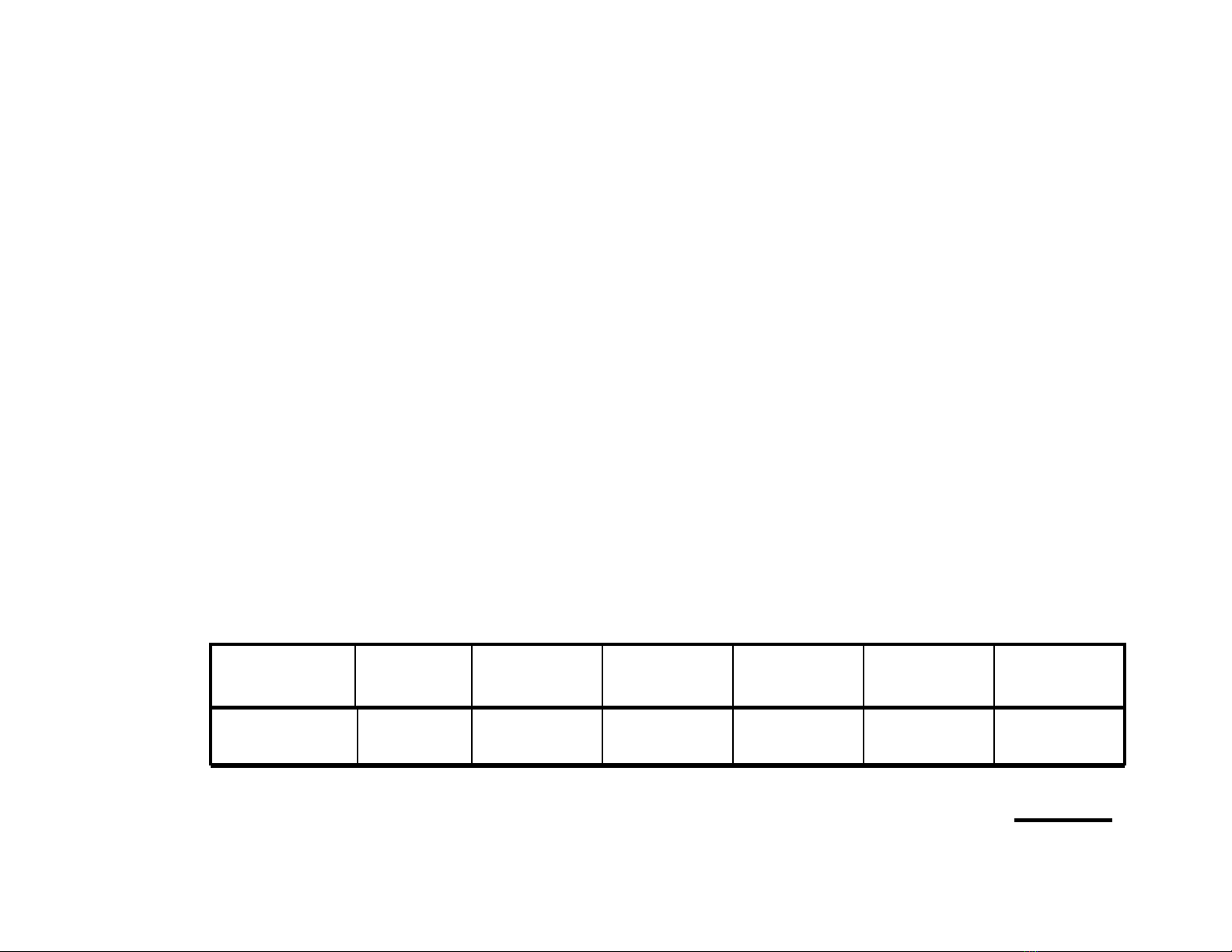
1x2
2
+ 0x2
1
+ 1x2
0
+ 0x2
^1
+1x2
^2
+ 1x2
^3
= 5.375
2
^3
2
^2
2
^1
.2
0
2
1
2
2
^3^2^1.012
Ví dF:
Giá trG :