Lý thuy t t ng đ i r ngế ươ ố ộ
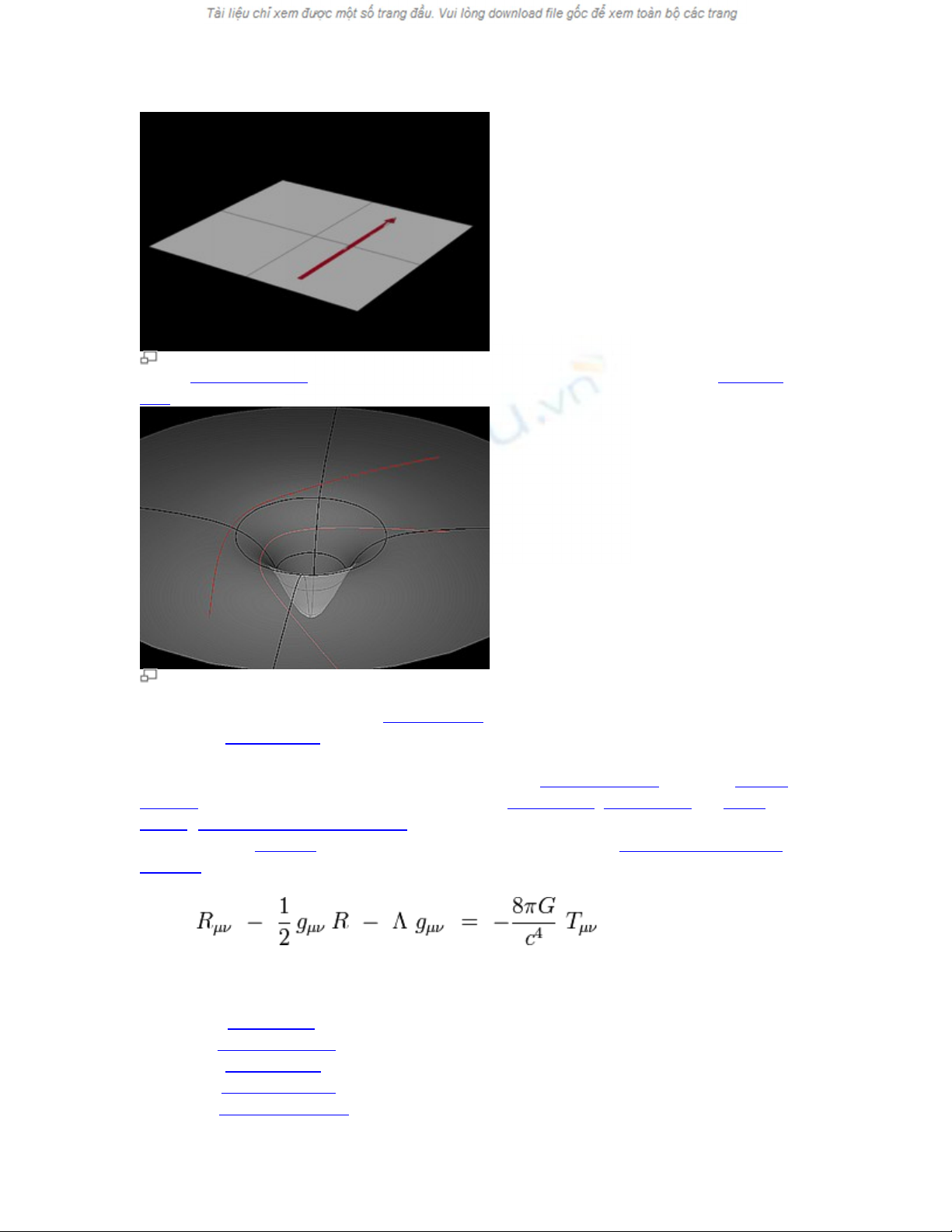
Hình nh hai chi u v s bi n d ng c a không th i gian. S t n t i c a v t ch t làmả ề ề ự ế ạ ủ ờ ự ồ ạ ủ ậ ấ
bi n đ i hình dáng c a không th i gian, s cong c a nó có th đ c coi là h p d nế ổ ủ ờ ự ủ ể ượ ấ ẫ
Lý thuy t t ng đ i r ngế ươ ố ộ , còn đ c g i là ượ ọ lý thuy t t ng đ i t ng quátế ươ ố ổ , là m tộ
lý thuy tế v t lýậ c b n v ơ ả ề h p d nấ ẫ . Lý thuy t này đ c ế ượ Albert Einstein đ a ra vàoư
năm 1915. Nó có th coi là ph n b sung và m r ng c a ể ầ ổ ở ộ ủ lý thuy t h p d n Newtonế ấ ẫ ở
t m vĩ mô và v i v n t c l n.ầ ớ ậ ố ớ
Lý thuy t này mô t h p d n t ng t nh s bi n d ng đ a ph ng c a ế ả ấ ẫ ươ ự ư ự ế ạ ị ươ ủ không-th iờ
gian. C th là m t v t có ụ ể ộ ậ kh i l ngố ượ s làm cong ẽkhông th i gianờ xung quanh nó. Độ
cong c a không th i gian chính b ng l c h p d n. Nói m t cách khác, ủ ờ ằ ự ấ ẫ ộ h p d n là sấ ẫ ự
cong c a không th i gianủ ờ .
T khi ra đ i đ n nay, lý thuy t t ng đ i r ng đã ch a bao gi th t b i trong vi cừ ờ ế ế ươ ố ộ ư ờ ấ ạ ệ
gi i thích các k t qu th c nghi m. Nó là c s nghiên c u c a các ngành ả ế ả ự ệ ơ ở ứ ủ thiên văn
h cọ, vũ tr h cụ ọ và v t lý thiên vănậ. Nó gi i thích đ c r t nhi u các hi n t ng màả ượ ấ ề ệ ượ
v t lý c đi nậ ổ ể không th làm đ c v i đ chính xác và tin c y r t cao, ví d nh hi nể ượ ớ ộ ậ ấ ụ ư ệ
t ng ánh sáng b b cong khi đi g n ượ ị ẻ ầ M t Tr iặ ờ , ho c tiên đoán đ c s t n t i c aặ ượ ự ồ ạ ủ
sóng h p d nấ ẫ , h đenố và s giãn n c a vũ trự ở ủ ụ.
Không gi ng nh các lý thuy t v t lý cách m ng khác, nh ố ư ế ậ ạ ư c h c l ng tơ ọ ượ ử ch ngẳ
h n, lý thuy t t ng đ i ch do m t mình Albert Einstein xây d ng nên, m c dù ôngạ ế ươ ố ỉ ộ ự ặ
cũng c n s giúp đ c a m t ng i b n là ầ ự ỡ ủ ộ ườ ạ Marcel Grossmann v toán h c các m tề ọ ặ
cong.
Gi i thi uớ ệ
Trong c h c Newtonơ ọ không gian là ph ng và hai v t th hút nhau nh vào ẳ ậ ể ờ l c h pự ấ
d nẫ
Trong lý thuy t t ng đ i r ng, các kh i l ng làm cong không gian xung quanh nó.ế ươ ố ộ ố ượ
H qu c a s cong này t o ra ệ ả ủ ự ạ l c quán tínhự, gi ng nh h qu c a hai v t th hútố ư ệ ả ủ ậ ể
nhau b ng ằl c h p d nự ấ ẫ .
Lý thuy t t ng đ i r ng, d ng thu n túy, mô t ế ươ ố ộ ở ạ ầ ả không th i gianờ nh m t ư ộ đa t pạ
Lorentz 4 chi u, b làm cong b i s có m t c a ề ị ở ự ặ ủ kh i l ngố ượ , năng l ngượ , và xung
l ngượ (tenx ng su t năng l ngơ ứ ấ ượ ) n m trong nó. M i liên h gi a tenx ng su tằ ố ệ ữ ơ ứ ấ
năng l ng và ượ đ congộ c a không th i gian đ c bi u th qua ủ ờ ượ ể ị ph ng trình tr ngươ ườ
Einstein.
Trong đó:
•Rμν: tenx Ricciơ
•R: vô h ng Ricciướ
•gμν: tenx mêtricơ
•Λ : h ng s vũ trằ ố ụ
•c : v n t c ánh sángậ ố trong chân không
•G : h ng s h p d nằ ố ấ ẫ (gi ng nh h ng s h p d n trong ố ư ằ ố ấ ẫ đ nh lu t h p d nị ậ ấ ẫ c aủ
Newton)
•Tμν : tenx năng l ng-xung l ngơ ượ ượ
Chuy n đ ng quán tính c a v t th là chuy n đ ng theo các ể ộ ủ ậ ể ể ộ đ ng tr c đ aườ ắ ị (đ ngườ
tr c đ a ki u th i gianắ ị ể ờ cho các v t có kh i l ng và ậ ố ượ đ ng tr c đ a ki u ánh sángườ ắ ị ể cho
photon) trong không th i gian và hoàn toàn ph thu c vào đ cong c a không th i gian.ờ ụ ộ ộ ủ ờ
Đ c đi m khác bi t nh t c a lý thuy t t ng đ i r ng so v i các lý thuy t khác là ýặ ể ệ ấ ủ ế ươ ố ộ ớ ế
t ng v ưở ề l c h p d nự ấ ẫ đ c thay b ng hình dáng c a không th i gian. Các hi n t ngượ ằ ủ ờ ệ ượ
mà c h c c đi n mô t là tác đ ng c a l c h p d n (nh chuy n đ ng c a các ơ ọ ổ ể ả ộ ủ ự ấ ẫ ư ể ộ ủ hành
tinh quanh M t Tr iặ ờ ) thì l i đ c xem xét nh là ạ ượ ư chuy n đ ng theo quán tínhể ộ trong
không th i gian cong trong lý thuy t t ng đ i r ng.ờ ế ươ ố ộ
Xét ví d v m t ng i chuy n đ ng trên qu đ o quanh ụ ề ộ ườ ể ộ ỹ ạ Trái Đ tấ. Ng i đó s c mườ ẽ ả
th y ấphi tr ng l ngọ ượ gi ng nh khi b ố ư ị r i t doơ ự xu ng Trái Đ t. Trong lý thuy t h pố ấ ế ấ
d n Newton, chuy n đ ng c a ng i đó là do ẫ ể ộ ủ ườ l c h p d nự ấ ẫ gi a ng i này và Trái Đ tữ ườ ấ
t o nên ạl c h ng tâmự ướ cho ng i đó quay xung quanh Trái Đ t. Trong lý thuy t t ngườ ấ ế ươ
đ i r ng, tình hu ng trên đ c gi i thích khác h n. Trái Đ t làm bi n d ng không th iố ộ ố ượ ả ẳ ấ ế ạ ờ
gian và ng i du hành s chuy n đ ng theo quán tính trong không th i gian; nh ngườ ẽ ể ộ ờ ư
hình chi u c a đ ng tr c đ a trong không th i gian lên không gian 3 chi u cho th yế ủ ườ ắ ị ờ ề ấ
nh th Trái Đ t tác d ng m t l c gi ng i này trên qu đ o.ư ể ấ ụ ộ ự ữ ườ ỹ ạ
Th c ra, ng i chuy n đ ng trên qu đ o cũng làm cong không th i gian xung quanhự ườ ể ộ ỹ ạ ờ
anh ta, nh ng đ cong này r t nh so v i đ cong mà Trái Đ t t o ra.ư ộ ấ ỏ ớ ộ ấ ạ
Vì không-th i gian liên quan đ n v t ch t nên n u không có v t ch t thì vi c xác đ nhờ ế ậ ấ ế ậ ấ ệ ị
không-th i gian không đ c chính xác. Chính vì th ng i ta c n các gi thuy t đ cờ ượ ế ườ ầ ả ế ặ
bi t nh là các ệ ư tính đ i x ngố ứ đ có th thao tác các không-th i gian kh dĩ, sau đó m iể ể ờ ả ớ
tìm xem v t ch t c n ph i n m đâu đ xác đ nh các tính ch t h p lý,... Các ậ ấ ầ ả ằ ở ể ị ấ ợ đi uề
ki n biênệ (còn g i là ọđi u ki n ban đ uề ệ ầ ) có th là v n đ khó khăn. ể ấ ề Sóng h p d nấ ẫ có
th vi ph m ý t ng không-th i gian đ c xác đ nh m t l n cho mãi mãi.ể ạ ưở ờ ượ ị ộ ầ
Các nguyên lý n n t ngề ả
Lý thuy t t ng đ i r ng d a trên các nguyên lý n n t ng:ế ươ ố ộ ự ề ả
•Nguyên lý hi p bi nệ ế : các đ nh lu t v t lý là nh nhau trong t t các các ị ậ ậ ư ấ h quyệ
chi uế (các đ nh lu t v t lý là các ph ng trình tenx ). ị ậ ậ ươ ơ
•Chuy n đ ng quán tínhể ộ theo đ ng tr c đ aườ ắ ị .
Nguyên lý t ng đ ngươ ươ , v n là đi m kh i đ u trong quá trình xây d ng lý thuy tố ể ở ầ ự ế
t ng đ i r ng t ươ ố ộ ừ thuy t t ng đ i h pế ươ ố ẹ , sau này đ c nh n ra là h qu c a nguyênượ ậ ệ ả ủ
lý hi p bi n và nguyên lý chuy n đ ng quán tính theo đ ng tr c đ a. Nguyên lý nàyệ ế ể ộ ườ ắ ị
phát bi u r ng, không có m t thí nghi m t i không th i gian đ a ph ng nào có thể ằ ộ ệ ạ ờ ị ươ ể
phân bi t s r i t do không quay trong tr ng h p d n v i chuy n đ ng th ng đ uệ ự ơ ự ườ ấ ẫ ớ ể ộ ẳ ề
khi không có tr ng h p d n. Nó cũng d n đ n k t qu quan tr ng là đ cong khôngườ ấ ẫ ẫ ế ế ả ọ ộ
th i gian gây nên b i s có m t c a v t ch t, ờ ở ự ặ ủ ậ ấ ph ng trình tr ng Einsteinươ ườ .
Ki m ch ngể ứ
Gi ng nh t t c các ố ư ấ ả lý thuy t khoa h cế ọ , lý thuy t t ng đ i r ng c n ph i có cácế ươ ố ộ ầ ả
tiên đoán và ph i đ c ki m ch ng b ng các k t qu th c nghi m. M t s các tiênả ượ ể ứ ằ ế ả ự ệ ộ ố
đoán c a lý thuy t này g m có s d ch chuy n g n ủ ế ồ ự ị ể ầ đi m c n nh tể ậ ậ c a qu đ o c aủ ỹ ạ ủ
các hành tinh (đ c bi t là ặ ệ Sao Th yủ), s l ch c a ánh sáng khi đi g n các v t th cóự ệ ủ ầ ậ ể
kh i l ng l n, và s t n t i c a sóng h p d n. Hai tiên đoán đ u tiên đã đ c ki mố ượ ớ ự ồ ạ ủ ấ ẫ ầ ượ ể
tra v i đ chính xác và tin t ng cao. Ph n l n các nhà v t lý đ u tin vào s t n t iớ ộ ưở ầ ớ ậ ề ự ồ ạ
c a sóng h p d n nh ng s t n t i c a nó ch a đ c kh ng đ nh tr c ti p. Tuy nhiênủ ấ ẫ ư ự ồ ạ ủ ư ượ ẳ ị ự ế
các hi u ng gián ti p đã đ c quan sát trong nhi u h sao đôi.ệ ứ ế ượ ề ệ
M t s tiên đoán khác g m ộ ố ồ s giãn n c a vũ trự ở ủ ụ, s t n t i c a ự ồ ạ ủ h đenố và kh năngả
t n t i c a các ồ ạ ủ l giunỗ, h tr ngố ắ . Ngày nay, s t n t i c a h đen nói chung là đãự ồ ạ ủ ố
đ c ch p nh n r ng rãi, nh ng kh năng t n t i c a các l giun thì v n còn gây tranhượ ấ ậ ộ ư ả ồ ạ ủ ỗ ẫ
cãi. Nhi u ềnhà khoa h cọ tin là các l giun ch có th t n t i khi xu t hi n ỗ ỉ ể ồ ạ ấ ệ v t ch tậ ấ
ngo i laiạ. Tiên đoán v ềh tr ngố ắ có v r t xa v i, vì nó d ng nh trái v i ẻ ấ ờ ườ ư ớ đ nh lu tị ậ
hai nhi t đ ng l c h cệ ộ ự ọ .
Các tiên đoán đ nh l ng khác c a lý thuy t t ng đ i r ng đã đ c kh ng đ nh b ngị ượ ủ ế ươ ố ộ ượ ẳ ị ằ
các quan sát thiên văn. M t trong nh ng quan sát g n đây là vi c phát hi n ra chùm saoộ ữ ầ ệ ệ
đôi neutron PSR J0737-3039 vào năm 2003 trong đó s ựti n đ ngế ộ c n nh t là 16.88°ậ ậ
m t năm (t c là nhanh h n c a Sao Th y kho ng 140.000 l n) ộ ứ ơ ủ ủ ả ầ [1] [2].
Tính phi Euclide c a không-th i gian cũng có th đ c ki m ch ng m t cách tr củ ờ ể ượ ể ứ ộ ự
ti p. Ví d , ế ụ thí nghi m Pound-Rebkaệ vào năm 1959 đã ghi nh n đ c s thay đ i b cậ ượ ự ổ ướ
sóng ánh sáng t m t ngu n ừ ộ ồ cô ban do nh h ng c a h p d n. ả ưở ủ ấ ẫ Đ ng h nguyên tồ ồ ử
trên v tinh c a ệ ủ h th ng đ nh v toàn c uệ ố ị ị ầ (GPS) đ c đi u ch nh l i do h p d n c aượ ề ỉ ạ ấ ẫ ủ
Trái Đ t đ phù h p v i đ ng h trên m t đ t.ấ ể ợ ớ ồ ồ ặ ấ
Các tiên đoán nh là ưd ch chuy n đị ể ỏ h p d n, các ngôi sao b cong h ng truy n c aấ ẫ ẻ ướ ề ủ
ánh sáng, các h đenố, s ch m d n c a th i gian trong tr ng h p d n, s a đ i chút ítự ậ ầ ủ ờ ườ ấ ẫ ử ổ
v ềđ nh lu t h p d nị ậ ấ ẫ trong tr ng h p d n y u cũng đ u ch a b m t thí nghi m nàoườ ấ ẫ ế ề ư ị ộ ệ
ph n bác.ả
Toán h c c a lý thuy t t ng đ i r ngọ ủ ế ươ ố ộ
Toán h c c a lý thuy t t ng đ i r ng ch y u là ọ ủ ế ươ ố ộ ủ ế đ i s tensorạ ố và hình h c phiọ
Euclide trên không gian Riemann n-chi u, phát tri n t năm ề ể ừ 1854, b i ởBernhard
Riemann. Vi c dùng các ệtensor đã đ n gi n hóa r t nhi u các tính toán và th hi n m tơ ả ấ ề ể ệ ộ
th c t là t t c các quan sát là t ng đ ng khi mô t các đ nh lu t v t lý.ự ế ấ ả ươ ươ ả ị ậ ậ
M t tensor quan tr ng trong thuy t t ng đ i là ộ ọ ế ươ ố tensor Riemann, đó là m t ộma tr nậ số
đo đ l ch c a m t ộ ệ ủ ộ véc tơ khi chuy n đ ng d c theo m t b m t song song v i chínhể ộ ọ ộ ề ặ ớ
nó sau khi đi đ c m t vòng. Trong không gian ph ng, các véc t s tr l i h ng c aượ ộ ẳ ơ ẽ ở ạ ướ ủ
nó (tensor Riemann b ng không), nh ng trong không gian cong thì nó l i không làmằ ư ạ
đ c đi u đó (nói chung tensor Riemann khác không). Trong các không gian hai chi u,ượ ề ề
tensor Riemann là m t ma tr n ộ ậ (t c là s th c) đ c g i là đ cong Gauss hayứ ố ự ượ ọ ộ
đ cong vô h ngộ ướ . Đ cong có th đ c đo hoàn toàn trên m t b m t và nó cũngộ ể ượ ộ ề ặ
t ng t đ i v i các m t nhi u chi u h n nh là không gian ho c không-th i gian.ươ ự ố ớ ặ ề ề ơ ư ặ ờ
Đ ng l c h c c a lý thuy t t ng đ i r ng liên quan đ n các ộ ự ọ ủ ế ươ ố ộ ế ph ng trình Einsteinươ ,
m t ph ng trình tensor mô t quá trình v t ch t nh h ng đ n hình dáng c aộ ươ ả ậ ấ ả ưở ế ủ
không-th i gian, m t ph ng trình chuy n đ ng mô t quá trình các v t th chuy nờ ộ ươ ể ộ ả ậ ể ể
đ ng trong không gian b cong đó. Thông th ng, ng i ta th ng dùng các phép g nộ ị ườ ườ ườ ầ
đúng khi làm vi c v i các ph ng trình này.ệ ớ ươ
Các ph ng trình Einsteinươ là các ph ng trình vi phân riêng ph nươ ầ phi tuy nế cho các hệ
metric. Đi u này phân bi t các ph ng trình này v i các ph ng trình tr ng khácề ệ ươ ớ ươ ườ
trong v t lý (ví d , h ậ ụ ệ ph ng trình Maxwellươ là h ệtuy n tínhế trong tr ng đi n t ,ườ ệ ừ
ph ng trình Schrodingerươ là tuy n tính v i các ế ớ hàm sóng). Đó cũng chính là đi m khácể
nhau căn b n c a lý thuy t t ng đ i r ng v i các lý thuy t v t lý khác.ả ủ ế ươ ố ộ ớ ế ậ
Liên h v i các lý thuy t v t lý khácệ ớ ế ậ
Lý thuy t t ng đ i h pế ươ ố ẹ
Trong lý thuy t t ng đ i h pế ươ ố ẹ , t t c các ấ ả s ki nự ệ đ u đ c quy v m t, hay nhi uề ượ ề ộ ề
h n m t, ơ ộ h quy chi uệ ế . M t h quy chi u đ c xác đ nh b ng vi c ch n h c s độ ệ ế ượ ị ằ ệ ọ ệ ơ ở ể
xác đ nh nó. Do đó, t t c các chuy n đ ng đ u đ c xác đ nh và đ nh l ng t ngị ấ ả ể ộ ề ượ ị ị ượ ươ
đ i v i nhau. Trong lý thuy t t ng đ i r ng, các h quy chi u có th đ c m r ngố ớ ế ươ ố ộ ệ ế ể ượ ở ộ
đ n vô h n theo t t c các h ng trong không-th i gian. Lý thuy t t ng đ i h pế ạ ấ ả ướ ờ ế ươ ố ẹ
nghiên c u chuy n đ ng c a các v t th trong các h quy chi u chuy n đông th ngứ ể ộ ủ ậ ể ệ ề ể ẳ
đ u v i nhau (t c là h quy chi u quán tính), trong khi đó, lý thuy t t ng đ i r ngề ớ ứ ệ ế ế ươ ố ộ
l i nghiên c u t t c các lo i h quy chi u. Lý thuy t t ng đ i r ng th a nh n r ngạ ứ ấ ả ạ ệ ế ế ươ ố ộ ừ ậ ằ
chúng ta ch có th xác đ nh đ c các h quy chi u c c b v i m t đ chính xác nh tỉ ể ị ượ ệ ế ụ ộ ớ ộ ộ ấ
đ nh trong m t kho ng th i gian h u h n và trong m t vùng không gian h u h n. Đi uị ộ ả ờ ữ ạ ộ ữ ạ ề
này t ng t nh vi c chúng ta v b n đ b m t Trái Đ t nh ng chúng ta không thươ ự ư ệ ẽ ả ồ ề ặ ấ ư ể
m r ng đ bao quát toàn b b m t mà không bi n d ng nó.ở ộ ể ộ ề ặ ế ạ
Lý thuy t t ng đ i h p đ a ra các ph ng trình v chuy n đ ng c a các v t thế ươ ố ẹ ư ươ ề ể ộ ủ ậ ể
chuy n đ ng khác nhau trên c s m t h ng s là ể ộ ơ ở ộ ằ ố v n t c ánh sángậ ố , đó là m t ộb tấ
bi nế trong các h quy chi u chuy n đ ng th ng đ u t ng đ i v i nhau. H qu c aệ ế ể ộ ẳ ề ươ ố ớ ệ ả ủ
đi u này là v t lý không th tách ề ậ ể không gian và th i gianờ kh i nhau mà ph i xét chúngỏ ả
nh th m t h b n chi u "không-th i gian". H này đ c chia thành hai lo i h ngư ể ộ ệ ố ề ờ ệ ượ ạ ướ
là "h ng ki u th i gian" và "h ng ki u không gian" ph thu c vào chuy n đ ngướ ể ờ ướ ể ụ ộ ể ộ
c a ng i quan sát. Lý thuy t t ng đ i r ng b sung thêm là không-th i gian c c bủ ườ ế ươ ố ộ ổ ờ ụ ộ
có th b b cong do kh i l ng c a v t ch t trong đó. Do đó, đ ng th ng trongể ị ẻ ố ượ ủ ậ ấ ườ ẳ