Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
97
MÔ HÌNH TÍNH TOÁN MÔ PHỎNG QUÁ TRÌNH
BẤT ỔN ĐỊNH KELVIN-HELMHOLTZ
Nguyễn Đức Hậu1, Nguyễn Thị Lý1, Sylvain Guillou2 và Kim Dan Nguyen3
2Đại học Thủy lợi, email: ndhau.dhtl@tlu.edu.vn
2Université de Caen, email: sylvain.guillou@unicaen.fr
3Saint-Venant Laboratory for Hydraulics, email: dan.nguyen@saint-venant-lab.fr
1. GIỚI THIỆU CHUNG
Trong bài báo này chúng tôi dùng mô hình
tính toán dòng chảy hai pha để mô phỏng sự
hình thành và phát triển của sự bất ổn định
Kelvin-Helmholtz. Bài toán được xét trên
một kênh hở tuần hoàn theo hướng của trục
Ox
. Kích thước của kênh là
3m
chiều dài và
3m
chiều cao, lớp trên là một lớp nước và
lớp dưới là một lớp bùn cát. Ở điều kiện ban
đầu áp đặt vận tốc nằm ngang của dòng chảy.
Trường vận tốc có một điểm uốn tại giao
diện của nước và bùn cát. Mô hình được tính
toán trên lưới chia đều với số nút lưới là
301 301
.
2. PHƯƠNG PHÁP NGHIÊN CỨU
(a) Mô hình hai pha
Trong mô hình dòng chảy hai pha chúng
tôi sử dụng mô hình Euler-Euler để biểu diễn
các hệ phương trình dòng chảy của các hạt
lỏng và các hạt rắn. Xuất phát từ hệ phương
trình Navier-Stokes, chúng tôi dùng các công
thức của Drew & Lahey [2] để xây dựng các
phương trình bảo toàn khối lượng và phương
trình chuyển động.
b) Cấu hình bài toán nghiên cứu
Bài toán được tính toán trên một kênh hở
tuần hoàn theo hướng của trục
Ox
. Kích
thước của kênh được xác định là hình vuông
với
3m
chiều dài và
3m
chiều cao, lớp trên
là một lớp nước và lớp dưới là một lớp bùn
cát. Tỉ khối của nước được xác định là
3
01000 /kg m
, tỉ khối của hạt chất rắn là
3
11360 /kg m
và độ nhớt động lực
010Pas
. Ở điều kiện ban đầu áp đặt vận
tốc nằm ngang
()uz
của dòng chảy và nồng
độ khối
. Chúng được xác định bởi
(xem hình 1).
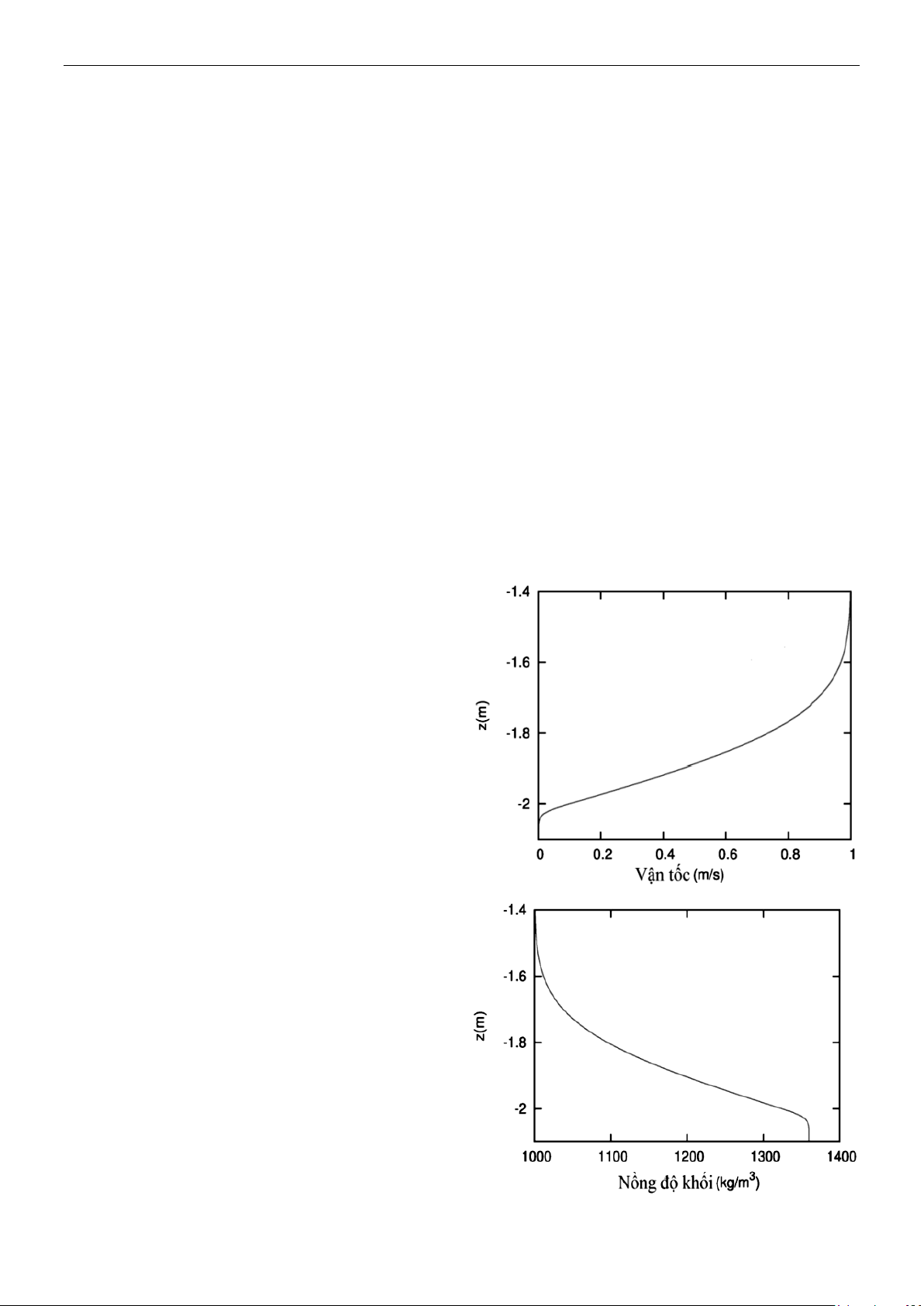
Hình 1. Trường vận tốc và nồng độ khối
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
98
0
( ) , zh
u z U F



;
0 1 1
( ) , zh
zF



;
1 erf , 0
,
1 1 1 erf
yy
Fy y












ở đó
erf
là “error function”,
là độ dày của
phần mà vận tốc có thay đổi,
h
là độ dày của
lớp cát phía dưới,
là hằng số. Trong bài
toán này ta chọn
1hm
,
0.3m
và
0.1
.
3. KẾT QUẢ NGHIÊN CỨU
Trong [5] chúng tôi đã nghiên cứu với
trường hợp lưới thô
101 101
nút lưới ở đó
chúng ta đã thấy rằng sự bất ổn định
Kelvin-Helmholtz chỉ xuất hiện trong
trường hợp số Richardson
Ri
nhỏ hơn
0.25
điều này phù hợp với các kết quả nghiên
cứu trước đó của Milles [3]. Trong [6]
chúng tôi đã thực hiện mô phỏng với bốn
loại lưới thô, trung bình, lưới mịn và lưới
siêu mịn. So sánh các kết quả mô phỏng
nhận được đối với các loại lưới trong bài
báo này chúng tôi lựa chọn lưới mịn (F) với
301 301
nút lưới để nghiên cứu. Trong mô
phỏng này bước thời gian được chọn là
4
5 10
(s), vận tốc
02.5U
m/s tương ứng
với hằng số Richardson
0.113Ri
. Đường
kính của hạt chất rắn được mô phỏng là
50 m
(cát mịn).
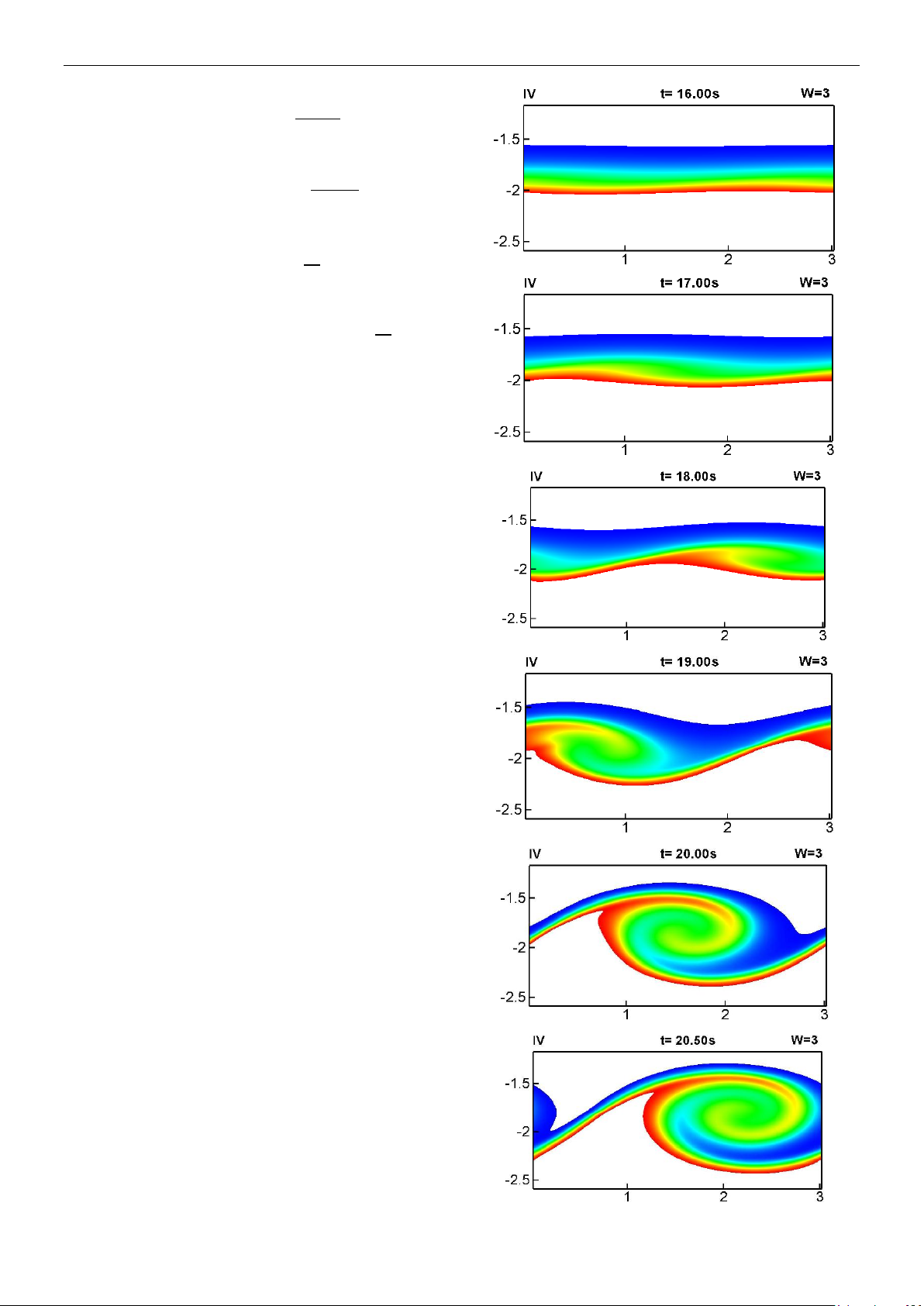
Hình 2 cho chúng ta thấy đường mức của
nồng độ khối mô phỏng tại các thời điểm
khác nhau. Từ thời điểm
17t
s ở bề mặt
xoáy bắt đầu được hình thành. Chú ý rằng
trong các thời điểm trước đó (trước
17t
s)
ở bề mặt vẫn còn ổn định. Sự bất ổn định
được tiếp tục hình thành và phát triển lớn
lên trong khoảng thời gian từ 17s đến
20.5s. Xoáy phát triển lớn nhất tại thời
điểm 20.5s.
Hình 2. Nồng độ khối
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
99
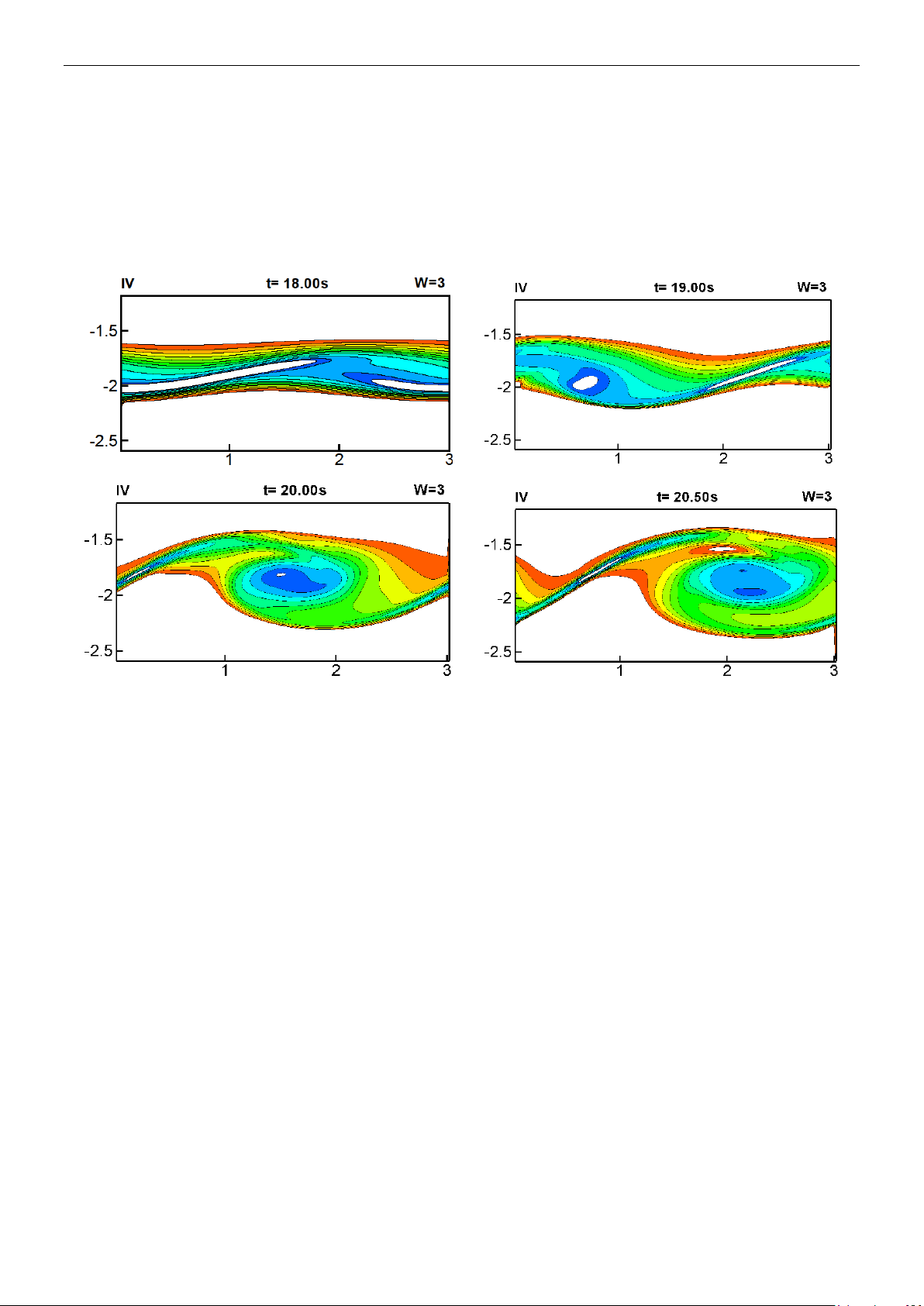
Hình 3 cho chúng ta thấy đường mức của
độ nhớt mô phỏng tại các thời điểm ứng với
hình 2. Bắt đầu từ thời điểm
18t
s độ nhớt
bắt đầu xuất hiện tuy nhiên chúng ta còn khó
có thể phân biệt ba vùng “noyau”,
“périphérique” và “cordon”. Ở thời điểm 19s
vùng “cordon” đã xuất hiện nhưng vẫn còn
dày, các vùng “noyau” và “périphérique” vẫn
chưa phát triển hoàn toàn. Chúng ta có thể
quan sát khá rõ 3 vùng đó tại thời điểm 20s:
Vùng “cordon” đã mảnh hơn và hai vùng
“noyau” và “périphérique” phát triển mạnh
mẽ. Tại thời điểm t= 20.5s các vùng phát
triển hoàn toàn và được quát sát rõ nét nhất.
Hình 3. Độ nhớt
4. KẾT LUẬN
Nhờ mô hình tính toán dòng chảy hai pha
chúng tôi đã mô phỏng sự hình thành và phát
triển của quá trình bất ổn định Kelvin-
Helmholtz xuất hiện ở bề mặt bùn cát khi tốc
độ dòng đủ lớn (số Richardson
Ri
nhỏ hơn
0.25
) và có điểm uốn tại bề mặt. Trong các
nghiên cứu tiếp theo chúng ta còn có thể xem
xét sự ảnh hưởng của kích thước hạt chất rắn
đến sự hình thành và phát triển sự bất ổn định
Kelvin-Helmholtz.
5. TÀI LIỆU THAM KHẢO
[1] Caulfield, C. P., and W. R. Peltier (2000),
The anatomy of the mixing transition in
homogeneous and stratified free shear layers,
Journal of Fluid Mechanics, 413, 1-47.
[2] Drew D.A. and Lahey R.T.: Analytical
Modelling of Multiphase Flow, in Particulate
Two-Phase Flow, ed. M.C. Roco,
Butterworth-Heinemann, Boston, (1993).
[3] Milles, J. W. (1961), On the stability of
heterogeneous shear flows, J. Fluid Mech,
10, 496-508.
[4] Nguyen D.H., Guillou S., Nguyen K.D.,
Pham Van Bang D., Chauchat J. (2012),
Simulation of dredged sediment releases
into homogeneous water using a two-phase
model. Advances in Water Resources 48
(2012) 102–112.
http://dx.doi.org/10.1016/j.advwatres.2012.
03.009.
[5] Nguyễn Đức Hậu, Nguyễn Thị Lý, Sylvain
Guillou, Kim Dan Nguyen (2013), Nghiên
cứu sự bất ổn định Kelvin-Helmholtz ở bề
mặt bùn cát, Tuyển tập hội nghị thường
niên 2013 của trường Đại học Thủy lợi.
[6] Nguyễn Đức Hậu, Nguyễn Thị Lý, Sylvain
Guillou, Kim Dan Nguyen (2014), Nghiên
cứu sự ảnh hưởng của lưới trong mô hình
tính toán sự bất ổn định Kelvin-Helmholtz,
Tuyển tập hội nghị thường niên 2014.
Trường Đại học Thủy lợi.
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
100