a) Khái niệm:
Mốt là biểu hiện của một lượng biến về tiêu thức nghiên cứu được gặp nhiều nhất
trong tổng thể.
Nếu xác định trên đồ thị với trục tung là tần số, trục hoành là lượng biến thì ta có
thể nói mốt là hoành độ của điểm có tung độ cao nhất.
b) Phương pháp xác định:
* Trường hợp 1: Đối với dãy số lượng biến không có khoảng cách tổ thì mốt là
lượng biến được gặp nhiều nhất trong dãy số lượng biến.
Thí dụ 2.1: Có tài liệu phân tổ sinh viên trong một lớp học (tiêu thức phân tổ là
tuổi).
Tuổi (xi) Số sinh viên (fi)
22
23
24
25
26
35
3
5
6
40
12
1
Kí hiệu: Mo là trị số của mốt
=> Mo = 25 vì lượng biến này có tần số
lớn nhất (f = 40)
Cộng 67
* Tr−êng hîp 2: §èi víi d·y l−îng biÕn cã kho¶ng c¸ch tæ th× mèt lµ l−îng biÕn mµ
trªn ®ã chøa mËt ®é ph©n phèi lín nhÊt, tøc lµ xung quanh l−îng biÕn Êy tËp trung tÇn sè
nhÒu nhÊt.
+ Tµi liÖu ph©n tæ cã kho¶ng c¸ch ®Òu nhau
C«ng thøc tÝnh:
fMo - fMo -1
Mo = xMo(min) + hMo -------------------------
(fMo- fMo -1) + (fMo- fMo +1)
Trong ®ã:
Mo : Ký hiÖu cña mèt
xMo (min): Giíi h¹n d−íi cña tæ chøa mèt
hMo: TrÞ sè cña kho¶ng c¸ch tæ chøa mèt
fMo: TÇn sè cña tæ chøc mèt
fMo–1: TÇn sè cña tæ ®øng tr−íc tæ chøa mèt
fMo + 1: TÇn sè cña tæ ®øng sau tæ chøa mèt
ThÝ dô: Cã tµi liÖu ph©n tæ mét lo¹i tr¸i c©y theo khèi l−îng nh− sau:
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 70
Khối lượng (g/quả) Số quả
80 – 84
84 – 88
88- 92
92 – 96
96 – 100
100 – 104
104 – 108
108 - 112
10
20
120
150
400
200
60
40
Cộng 1000
Yêu cầu xác định mốt của khối lượng quả?
→ Trước hết ta có thể xác định mốt vào tổ
thứ 5 (96 – 100) vì tổ này có tần số lớn
nhất (400 quả).
Từ đó ta xác định:
xMo (min) = 96 hMo = 4
fMo = 400 fMo-1 = 150 fMo + 1 = 200
Từ công thức (2) ta có Mo = 98,2 gam
+ Tµi liÖu ph©n tæ cã kho¶ng c¸ch tæ kh«ng ®Òu nhau, mèt vÉn ®−îc tÝnh theo c«ng
thøc trªn, nh−ng cÇn l−u ý lµ viÖc x¸c ®Þnh tæ chøa mèt kh«ng c¨n cø vµo tÇn sè mµ c¨n
cø vµo mËt ®é ph©n phèi.
C«ng thøc tÝnh mËt ®é ph©n phèi nh− sau:
hi
Mi = -------
fi
Trong ®ã:
Mi lµ mËt ®é ph©n phèi
fi lµ tÇn sè
hi lµ trÞ sè kho¶ng c¸ch tæ
* Tr−êng hîp 3: Sè ®¬n vÞ cña tæng thÓ nghiªn cøu cã khuynh h−íng tËp trung vµo
mét vµi l−îng biÕn nhÊt ®Þnh, tr−êng hîp nµy ta cã ®a mèt.
ThÝ dô: Cã tµi liÖu ph©n tæ s¾p xÕp cÆp vî chång theo sè con cña nh÷ng ng−êi ®ã
nh− sau:
Số con (xi) Số cặp vợ chồng (fi)
0
1
2
3
4
5
19
680
750
61
10
6
Cộng 1526
Yêu cầu xác định mốt của tổng thể nghiên cứu.
=> Qua tài liệu phân tổ, ta thấy số đơn vị có
khuynh hướng tập trung vào 2 lượng biến (1
con
và 2 con) như vậy trường hợp này mốt có 2 trị
số là 1 và 2.
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 71
c) Ý nghĩa của việc dùng mốt trong thống kê:
- Trong thống kê, mốt là chỉ tiêu có tác dụng bổ sung hoặc thay thế cho việc tính số
bình quân số học trong trường hợp việc xác định số trung bình số học gặp khó khăn.
Mốt cho ta thấy mức độ phát triển nhất của hiện tượng, mặt khác chỉ tiêu này không
chịu ảnh hưởng của các lượng biến giữa các đơn vị tổng thể như số trung bình số học.
Chẳng hạn khi nghiên cứu giá cả một mặt hàng nào đó trên thị trường, thông thường
người ta không có đủ tài liệu để xác định giá trị trung bình và có thể không cần tính giá
trị trung bình mà ta chỉ cần biết giá trị phổ biến nhất của mặt hàng nào đó.
- Mốt còn có tác dụng giúp cho các tổ chức sản xuất và thương nghiệp trong công
tác nghiên cứu xem các mặt hàng nào được tiêu thụ nhiều nhất, như cỡ giầy dép, cỡ kiểu
quần áo...
- Mốt không phụ thuộc vào giá trị ở hai đầu mút, thậm chí trong trường hợp giá trị
ở đầu mút nhỏ và giá trị ở cuối dãy số rất lớn thì giá trị của mốt cũng không bị ảnh
hưởng. Mốt có thể tính trong trường hợp lượng biến biến động trong phạm vi rất rộng
hoặc rất hẹp.
Tuy mốt có nhiều ưu điểm song mốt cũng không dùng nhiều như trung vị và trung
bình, có trường hợp không có mốt và không có giá trị xuất hiện nhiều nhất hoặc có
trường hợp có hai hoặc ba mốt ta không thể xác định được giá trị trung tâm chính xác.
3.4. Mối quan hệ giữa số trung bình cộng, số trung vị và mốt
Dựa vào số trung bình, số trung vị và mốt người ta có thể biết được hình dáng phân
phối của lượng biến trong tổng thể. Cụ thể là:
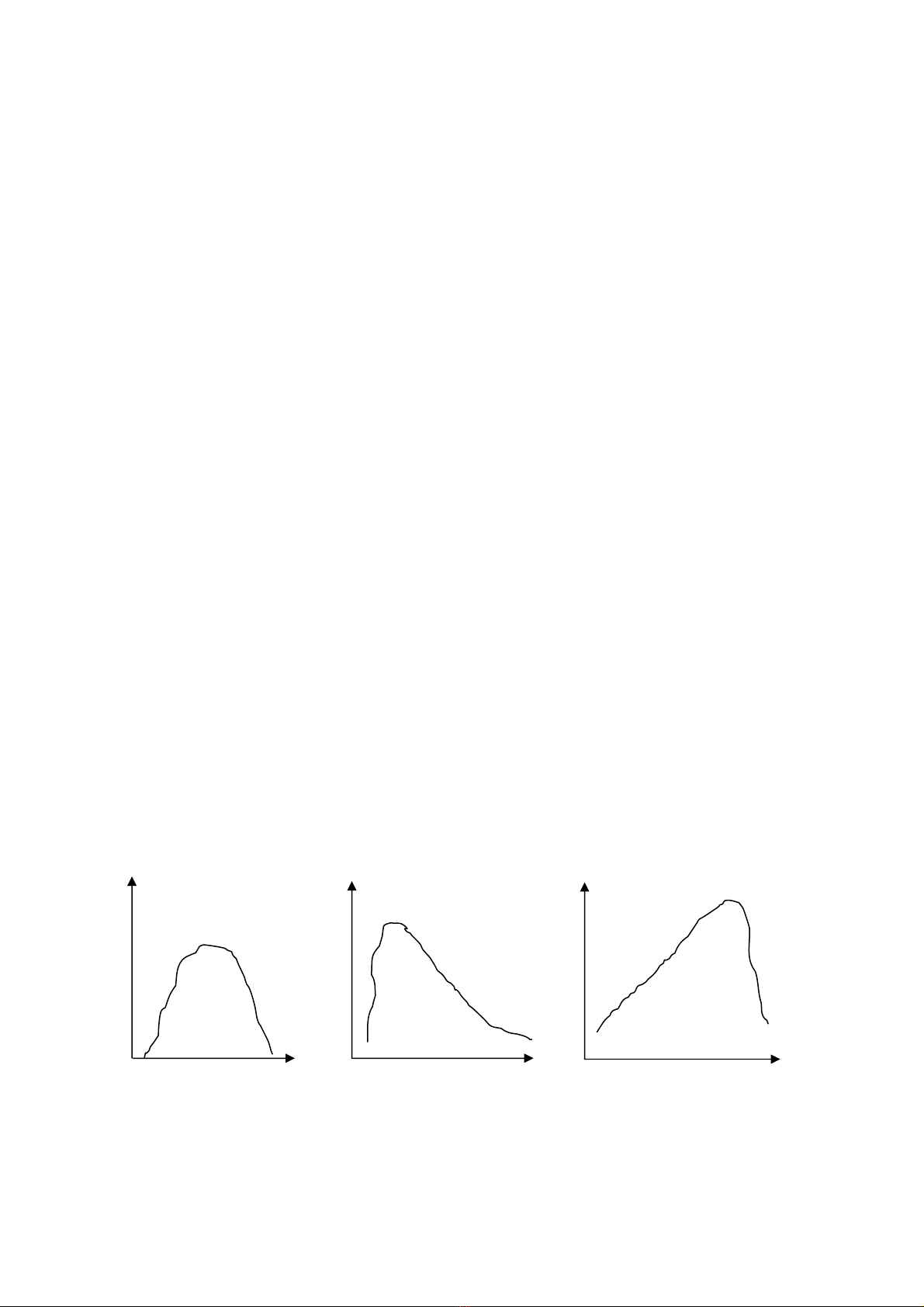
- Khi X b/q = Me = Mo thì phân phối đối xứng (phân phối chuẩn);
- Khi X b/q > Me > Mo thì phân phối lệch phải;
- Khi X b/q < Me < Mo thì phân phối lệch trái .
Điều này được thể hiện qua các đồ thị sau:
fi (tần số) fi fi
lệch phải lệch trái
Xi (lượng biến) Xi Xi
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 72
4. CÁC ĐẶC TRƯNG ĐO LƯỜNG ĐỘ PHÂN TÁN
4.1. Khái niệm
Thí dụ: Ta quan sát độ tuổi của 2 nhóm công nhân, mỗi nhóm gồm 5 người như sau:
Nhóm 1: 20 30 40 50 60 ⎯x1 = 40 tuổi
Nhóm 2: 38 39 40 41 42 ⎯x2 = 40 tuổi
Độ tuổi trung bình của 2 nhóm bằng nhau đều bằng 40 tuổi, nhưng ta chưa thể đánh
giá chính xác rằng mức độ đồng đều về tuổi tác của 2 nhóm này như thế nào.
Nếu ta quan sát từng lượng biến trong mỗi nhóm ta thấy nhóm 2 lượng biến biến
động ít và đồng đều hơn nhóm 1. Có thể nhận định rằng độ tuổi bình quân nhóm 2 đại
diện cao hơn nhóm 1. Do đó sự biến động lượng biến tiêu thức có liên quan rất lớn đến
mức độ đại biểu của số bình quân.
Sự biến động về lượng biến của các đơn vị tổng thể theo một tiêu thức nào đó gọi
là độ phân tán của hiện tượng.
Để đo mức độ phân tán hay mức độ đại biểu của số bình quân người ta đã tính ra
một loạt các đặc trưng gọi là các chỉ tiêu đo độ biến động tiêu thức.
4.2. Các chỉ tiêu đo độ biến động tiêu thức
a) Khoảng biến thiên (R) (còn gọi là toàn cự):
Khoảng biến thiên là độ lệch giữa lượng biến lớn nhất và lượng biến nhỏ nhất của
tiêu thức nghiên cứu trong tổng thể:
R = Xmax – Xmin.
Trong đó: Xmax là lượng biến lớn nhất; Xmin là lượng biến nhỏ nhất.
Ý nghĩa: R càng lớn độ biến động tiêu thức càng lớn, tính chất đại biểu của số bình
quân càng nhỏ và ngược lại.
Thí dụ: R1 = 60 - 20 = 40 R2 = 42 - 38 = 4
R1 > R2 ⎯x1 đại diện thấp hơn⎯x2
- Ưu điểm: Đơn giản, biểu hiện rõ và cụ thể phạm vi biến động.
- Nhược điểm: Do không xét đến các lượng biến ở giữa nên tính chất phản ánh
không đầy đủ, nhiều khi không nêu được tính biến động của tiêu thức.
b) Độ lệch tuyệt đối bình quân
⎯
d :
Độ lệch tuyệt đối bình quân là mức chênh lệch bình quân giữa các lượng biến và số
bình quân cộng của các lượng biến đó. Vì tổng độ lệch bằng không, nên khi tính toán
người ta phải lấy giá trị tuyệt đối của từng độ lệch.
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 73
Công thức tính như sau:
Σ|xi - ⎯x| Σ|xi - ⎯x| fi
⎯d = --------- hay ⎯d = -------------
n Σfi
Trong đó:
xi là lượng biến thứ i
x là số bình quân
n (Σfi) là số đơn vị tổng thể
Ý nghĩa: Độ lệch tuyệt đối bình quân càng nhỏ, độ biến thiên lượng biến càng ít,
tính đại biểu của số bình quân càng lớn và ngược lại.
Thí dụ trên:
⎯d1 = 60/5 = 12 ⎯d2 = 6/5 = 1,2
⎯d1 >⎯d2 nên ⎯x1 đại diện <⎯x2
- Ưu điểm: Thể hiện biến thiên của lượng biến chặt chẽ, đầy đủ hơn vì nó xét tới sự
chênh lệch của tất cả các lượng biến so với số bình quân.
- Nhược điểm: Bỏ qua sự khác nhau thực tế về dấu.
c) Phương sai (
δ
2):
Phương sai là số bình quân cộng của bình phương các độ lệch giữa các lượng biến
với số bình quân của các hiện tượng đó.
Công thức tính như sau:
Σ(xi - ⎯x)2 Σ(xi - ⎯x)2 fi
δ2 = ------------ hay δ2 = -------------
n Σfi
Trong đó:
xi là lượng biến thứ i
⎯x là số bình quân
n (Σfi) là số đơn vị tổng thể
Ý nghĩa: Phương sai càng bé thì mức độ biến động tiêu thức ít, tính chất đại biểu số
bình quân càng cao và ngược lại.
Phương sai được dùng nhiều nhất trong thực tế vì nó giải quyết được vấn đề về dấu
của các độ lệch tuyệt đối.
Thí dụ trên:
Ta lập bảng tính toán như sau:
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 74