Giaûng vieân: Th.S Leâ Xuaân Kyø
Bài giảng: Lý thuyếttínhiệu
9/7/2009 1
Chương 3
PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ
Nội dung:
3.1 Biếnđổi Fourier
3.1.1 Định nghĩa
3.1.2 Các tính chất
3.2 Phổcủamộtsốtín hiệu thông dụng
3.2.1 Phổcủatínhiệunăng lượng
3.3.2 Phổcủatínhiệucócôngsuất trung bình hữuhạn
3.3.3 Phổcủatínhiệutuần hoàn
3.3 Mậtđộ phổ
3.3.1 Mậtđộ phổnăng lượng
3.3.2 Mậtđộ phổcông suất
3.3.3 Mậtđộ phổcông suấtcủatínhiệutuần hoàn
Giaûng vieân: Th.S Leâ Xuaân Kyø
Bài giảng: Lý thuyếttínhiệu
9/7/2009 2
Chương 3 PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ
3.1 Biếnđổi Fourier
3.1.1 Định nghĩa
() () jt
X
xte dt
ω
ω
+∞
−
−∞
=∫
1
() ( )
2
jt
x
tXe
ω
d
ω
ω
π
+∞
−∞
=∫
(Biếnđổithuận)
(Biếnđổingược)
()
() () j
XXe
ϕ
ω
ωω
=
Phổthực
() () ()XPjQ
ω
ωω
=+
Phổảo
¾X(ω) đượcgọilàphổcủa tín hiệux(t). Kýhiệu: () ( )
F
xt X
ω
←⎯→
¾Tổng quát, phổX(ω) là một hàm phứcÆPhân tích thành các phổthành phần
Phổbiên độ Phổpha
Giaûng vieân: Th.S Leâ Xuaân Kyø
Bài giảng: Lý thuyếttínhiệu
9/7/2009 3
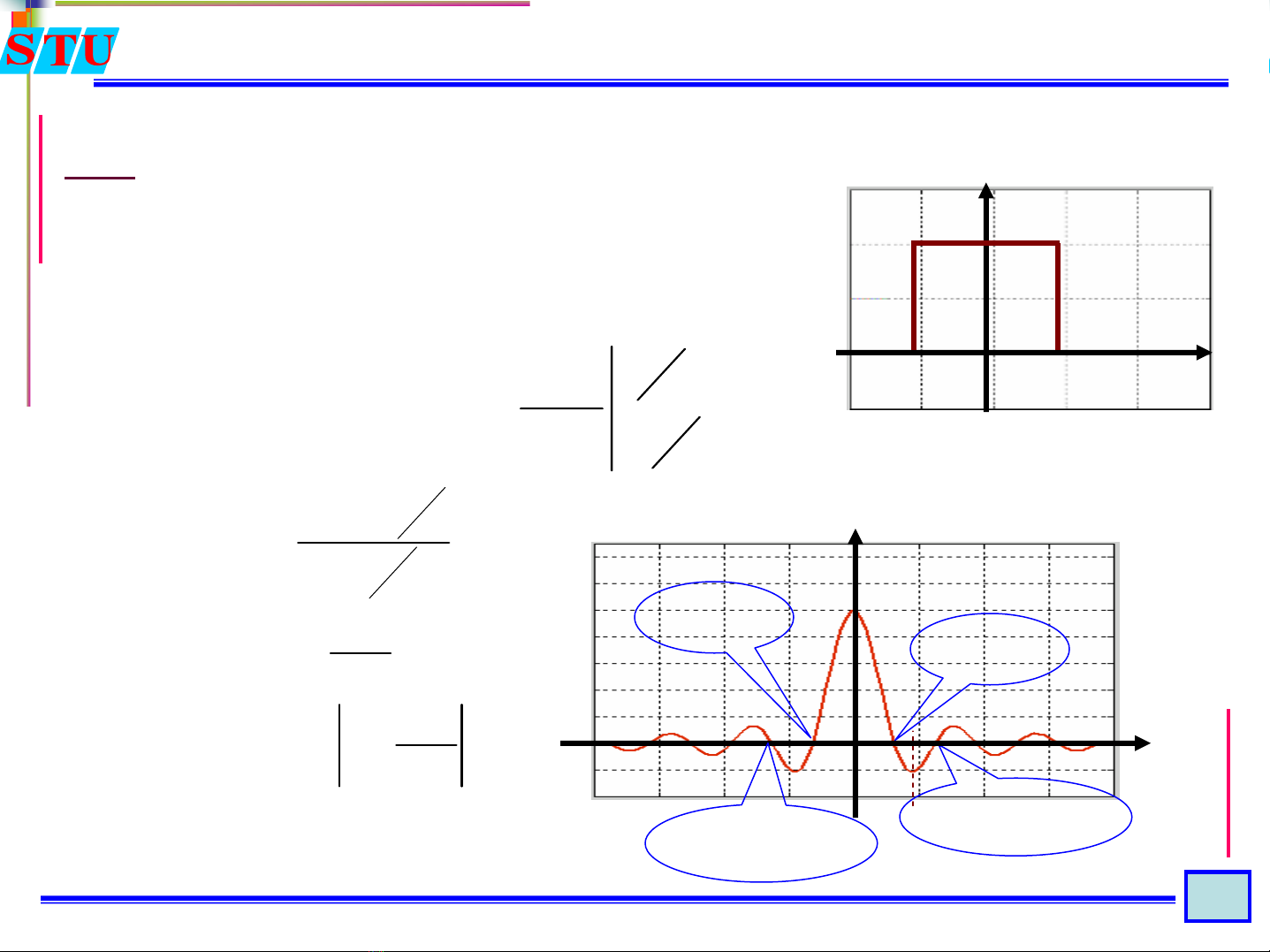
VD1:
Chương 3 PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ(tt)
Hãy xác định và vẽphổcủa tín hiệux(t)
Áp dụng công thứcbiếnđổi Fourier:
x(t)
t
0T/2-T/2
A
/2
/2
() ()
2
..
2
sin 2
.
2
2
|()| 2
jt
Tjt
jt
T
Xxtedt
T
e
Ae dt A T
j
T
AT T
T
ATSa
T
XATSa
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+∞
−
−∞
−
−
−
=
==
−−
=
=
⇒=
∫
∫
AT
0
ω
2
π
/T
4
π
/T
-4
π
/T
-2
π
/T
X(
ω
)
??? Vẽphổbiên độ và phổpha
Giaûng vieân: Th.S Leâ Xuaân Kyø
Bài giảng: Lý thuyếttínhiệu
9/7/2009 4
3.1.2 Tính chất
Chương 3 PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ(tt)
a. Tính chấtchẵnlẻ:
Nếu x(t) là hàm thực: phổbiên độ |X(
ω
)|: hàm chẵn
phổpha
ϕ
(
ω
): hàm lẻ
phổthựcQ(
ω
): hàm chẵn
phổảoP(
ω
): hàm lẻ
Quan hệ:
() ( );
() ( ) () ( )
() ()
F
FF
F
xt X
xt X x t X
xt X
ω
ω
ω
∗∗
∗∗
⎧
−
←⎯→−
⎪
←⎯→⇒ ←⎯→−
⎨
⎪−←⎯→
⎩
1
() 1() ( )
1
() 1() ()
t
t
xt e t X j
xt e t X j
α
α
ωαω
ω
α
ω
−
=↔=
+
⇒−= −↔ =−
VD2:
Giaûng vieân: Th.S Leâ Xuaân Kyø
Bài giảng: Lý thuyếttínhiệu
9/7/2009 5
Chương 3 PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ(tt)
11 2 2 1 2 2 1 2
() () ( ) ( ), ,
F
ax t ax t aX a X a a
ωω
+←⎯→+ ∀
3
() 3 2
tt
xt e e
−
−
=−
12
11
222
22
2
3& 2
2612
() ( ) ( )
119
6
() ( ) 9
tF
tF
aa
xt e X X
xt e X
ωω
ω
ωω
ωω
−
−
⎧
⎪==
⎪
⎪=←⎯→= ⇒=−
⎨+++
⎪
⎪=←⎯→=
⎪+
⎩
3.1.2 Tính chất (tt)
b. Tính chấttuyến tính:
Nếu
thì
112 2
() ( ); () ( )
FF
xt X xt X
ω
ω
←⎯→←⎯→
Ví dụ3: Xác định phổcủa tín hiệu sau: