BÀI T P PHÉP BI N HÌNH KH I 11Ậ Ế Ỗ
PHÉP BI N HÌNHẾ
*****
Câu 1: Trong m t ph ng Oxy cho M (2 ; 3), tìmặ ẳ
nh c a đi m M qua phép đ i x ng qua đ ngả ủ ể ố ứ ườ
th ng y - x = 0ẳ
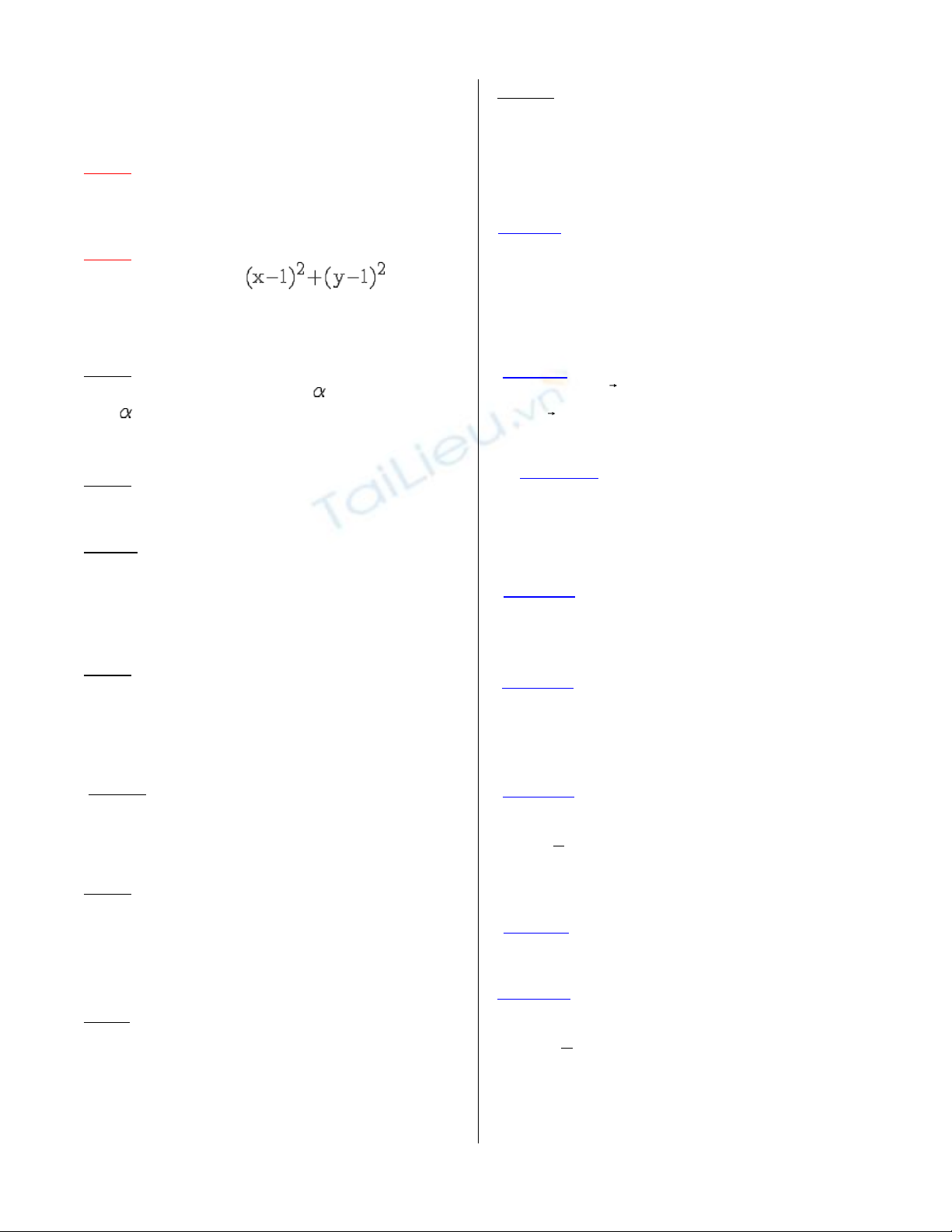
Câu 2: Trong m t ph ng Oxy, cho đ ng trònặ ẳ ườ
(C) có ph ng trình: ươ = 4, tìm
ph ng trình đ ng tròn (C’) nh c a ( C) quaươ ườ ả ủ
phép v t tâm O t s k = 2 ị ự ỉ ố
Câu 3: Cho hình vuông ABCD tâm O. Phép quay
Q có tâm quay O và góc quay . V i giá tr nàoớ ị
c a ủ, phép quay Q bi n hình vuông ABCDế
thành chính nó ?
Câu 4: N u ế
2IA AB=
uur uuur
thì phép v t tâm ị ự
I
bi nế
A
thành
B
theo t s ỉ ố
k
b ng bao nhiêu?ằ
Câu 5: Cho đ ng trònườ
2 2
( ) : 6 2 1 0C x y x y+ − + + =
. Tìm ph ng trìnhươ
đ ng tròn đ i x ng v i ườ ố ứ ớ
( )C
qua đ ng th ngườ ẳ
( ) : 0d x y− =
Câu 6 : Cho hai đ ng th ng ườ ẳ
( ) : 3 3 0k x y− − =
,
( ) : 0l x y+ =
. Phép đ i x ng tâm ố ứ I bi n ế
( )k
thành
( ') : 3 1 0k x y− + =
,
( )l
thành
( ') : 6 0l x y+ − =
. Tìm t a đ c a ọ ộ ủ I
Câu 7 : Tìm ph ng trình c a đ ng th ng đ iươ ủ ườ ẳ ố
x ng v i đ ng th ng ứ ớ ườ ẳ
( ) :3 4 5 0x y∆ − + =
qua
đi m ể
( )
1;2I−
Câu 8 : Cho đ ng trònườ
( ) ( )
2 2
( ) : 1 2 4C x y− + − =
. nh c a Ả ủ
( )C
qua
phép v t ị ự
2
O
V−
là đ ng tròn ườ
( ')C
có ph ngươ
trình
Câu 9 : Trong m t ph ng Oxy cho đi mặ ẳ ể
M( 2;1). Phép d i hình có đ c b ng cách th cờ ượ ằ ự
hi n liên ti p phép đ i x ng qua tâm O và phépệ ế ố ứ
t nh ti n theo vect ị ế ơ
(2;3)v
r
bi n M thành đi mế ể
N. Tìm t a đ đi m N ọ ộ ể
Câu 10 : Trong m t ph ng Oxy cho đi mặ ẳ ể
M(1;2). Phép đ ng d ng có đ c b ng cáchồ ạ ượ ằ
th c hi n liên ti p phép v t tâm O, t s v t kự ệ ế ị ự ỉ ố ị ự
= -2 và phép đ i x ng tâm O s bi n M thànhố ứ ẽ ế
các đi m N. Tìm t a đ c a Nể ọ ộ ủ
Câu 11: Trong m t ph ng v i h t a đặ ẳ ớ ệ ọ ộ
Oxy, cho đi m I(1;1) và đ ng th ng d:ể ườ ẳ
x + y + 2 = 0. Phép đ i x ng tâm I bi nố ứ ế
đ ng th ng d thành đ ng th ng d’ , tìmườ ẳ ườ ẳ
ph ng trình c a d’ươ ủ
Câu 12 Trong m t ph ng Oxy, cho đi m E(-ặ ẳ ể
3;5) và vect ơ
v
= ( 1; - 2). Phép t nh ti n theoị ế
vect ơ
v
bi n đi m F , tìm t a đ đi m Fế ể ọ ộ ể
Câu 13 : Trong măt phăng Oxy cho (d):
2x y 5 0− + + =
. Phep vi t tâm O ti sô ự
k 2=
biên đ ng thăng d thanh đ ng thăng d’ , tìm ườ ườ
ph ng trình c a d’ươ ủ
Câu 14 : Trong măt phăng Oxy, điêm
A( 3;1)−
, tìm anh cua điêm A qua phep đôi x ng qua ứ
đ ng th ng ườ ẳ
y x= ±
Câu 15 : Cho tam giác đ u ABC , O là tâmề
đ ng tròn ngo i ti p tam giác đó. V i giá trườ ạ ế ớ ị
nào sau đây c a góc ủ
ϕ
thì phép quay Q(O;
ϕ
)
bi n tam giác ABC thành chính nó ?ế
Câu 16 : Cho đ ng tròn (C) có ph ng trình:ườ ươ
x2+ y2 -2x + 6y - 4 = 0. nh c a (C) qua phép vẢ ủ ị
t Vự(O;
1
2
) là đ ng tròn (C') ,tìm ph ng trìnhườ ươ
c a ( C’)ủ
Câu 17 Cho M'(4;-3). G i M' = Qọ(o;900)(M). T aọ
đ c a M là bao nhiêu ? ộ ủ
Câu 1 9 : Cho đ ng tròn (C) có ph ng trình:ườ ươ
x2+ y2 -2x + 6y - 4 = 0. nh c a (C) qua phép vẢ ủ ị
t Vự(0;
1
2
−
) là đ ng tròn (C'), tìm ph ng trìnhườ ươ
c a ( C’)ủ
1
BÀI T P PHÉP BI N HÌNH KH I 11Ậ Ế Ỗ
Câu 20 . Cho đ ng th ng (D) đi qua hai đi mườ ẳ ể
A(1;3) và B(-2;5). Phép đ i x ng tâm I(2;3) bi nố ứ ế
đ ng th ng (D) thành đ ng th ng (Dườ ẳ ườ ẳ 1). Hãy
vi t ph ng trình đ ng th ng (Dế ươ ườ ẳ 1).
Câu 21: . cho hình l c giác đ u ABCDEF. Tìmụ ề
tr c và tâm đ i x ng c a hìnhụ ố ứ ủ
Câu 2 2 : . cho tam giác đ u ABC. Tìm tr c vàề ụ
tâm đ i x ng c a hìnhố ứ ủ
Câu 23: Trong m t ph ng Oxy cho M (2 ; -3),ặ ẳ
Tìm t a đ c a đi m là nh c a đi m M quaọ ộ ủ ể ả ủ ể
phép đ i x ng qua đ ng th ng y - 2x = 0 ố ứ ườ ẳ
Câu 24 : Trong m t ph ng Oxy cho b n đi mặ ẳ ố ể
A(-3;2), B(1;-2), C(2;5), D(-1;-3) .G i Aọ1 là nhả
c a A qua phép t nh ti n theo vectô ủ ị ế
BC
uuur
. G iọ
A2 là nh c a Aả ủ 1 qua phép đ i x ng t âmố ứ
D.Tìm t a đ Aọ ộ 2.
Câu 25: Trong hê truc toa đô Oxy.Goi V la phep
vi t tâm ự O ti sô -2 va T la phep tinh tiên theo
vecto
)2;1( −−=
→
u
, F la phep h p thanh cua ợ V
va T. Tim anh cua đ ng thăng ườ (d) -3x – 8y = 3
qua F
Câu 26: Trong măt phăng Oxy .Tim anh cua
đ ng troườ n (C):(x – 2)2 + (y – 4)2 = 16 qua viêc
th c hiên liên tiêp ự
Oy
Ð
va
→
v
T
v i ớ
)3;2(=
→
v
.
Câu 27 : Trong m t ph ng ặ ẳ
Oxy
cho
( ) ( )
2, 1 ; 3,2A B
−
. Tìm nh c a ả ủ
,A B
và đ ngườ
th ng ẳ
AB
qua phép đ i x ng :ố ứ
a) Tr c ụ
Ox
b) Tr c ụ
Oy
Câu 28
Trong m t ph ngặ ẳ
Oxy
cho đ ng th ng ườ ẳ d
,ph ng trình : ươ
2 5 0x y
+ − =
.
a) Vi t ph ng trình đ ng th ng ế ươ ườ ẳ d’ là nhả
c a ủd qua phép đ i x ng tr c ố ứ ụ Oy.
b/ Tìm t a đ đi m ọ ộ ể O’ là nh c a g c t a đả ủ ố ọ ộ
O qua phép đ i x ng tr c ố ứ ụ d.
Câu 29 :
Trong m t ph ngặ ẳ
Oxy
cho đ ng th ng d,ườ ẳ
ph ng trình : ươ
2 3 0x y
− − =
vàđ ng tròn ườ
( ) ( ) ( )
2 2
: 2 3 4C x y
− + − =
a/ Vi t ph ng trình đ ng tròn ế ươ ườ
( )
'C
là nhả
c a ủ
( )
C
qua phép đ i x ng tr c ố ứ ụ Ox.
b/Vi t ph ng trình đ ng tròn ế ươ ườ
( )
'C
là nhả
c a ủ
( )
C
qua phép đ i x ng tr c ố ứ ụ d.
Câu 30 : Tìm nh c a tam giác ả ủ ABC qua phép
đ i x ng tâm G, bi t G là tr ng tâmố ứ ế ọ
c a tam giác ủABC.
Câu 31: Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy cho
đi m ểA(2,-2) và đ ng th ng ườ ẳ d có ph ngươ
trình : 2x + y – 1 = 0 .
a. Tìm nh c a ả ủ A và d qua phép đ i x ng tâmố ứ
O
b. Tìm nh c a ả ủ d qua phép đ i x ng tâm ố ứ A.
Câu 32 :Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy cho
đi m ể
( ) ( ) ( )
1,2 ; 3,0 ; 3, 2A B C
− −
.
a. Tìm nh c a ả ủ A, B, C qua phép đ i x ngố ứ
tâm O.
b. Vi t ph ng trình đ ng tròn ngo i ti pế ươ ườ ạ ế
tam giác ABC.
c. Vi t ph ng trình đ ng tròn là nh c aế ươ ườ ả ủ
đ ng tròn ngo i ti p tam giác ườ ạ ế ABC qua phép
đ i x ng tâm ố ứ A.
Câu 33: Cho tam giác ABC. tr ng tâm ọG.
a. Tìm nh c a đi m ả ủ ể B qua phép quay
tâm A góc quay
0
90
.
b. Tìm nh c a đ ng th ng ả ủ ườ ẳ BC qua
phép quay tâm A góc quay
0
90
.
c. Tìm nh c a tam giác ả ủ ABC qua phép
quay tâm G góc quay
0
90
.
Câu 3 4 :
Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy cho đi m ểA(2,-2)
và đ ng th ng ườ ẳ d có ph ng trình : ươ 2x + y – 1
= 0 .
a./ Tìm nh c a ả ủ A và d qua phép quay tâm O
góc quay
0
90
.
b/ Tìm nh c a ả ủ d qua phép quay tâm A góc
quay
0
90
.
2
BÀI T P PHÉP BI N HÌNH KH I 11Ậ Ế Ỗ
Câu 3 5:
Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy cho đ ng trònườ
có ph ng trình : ươ
2 2
2 4 4 0x y x y+ − + − =
. Vi t ph ng trìnhế ươ
đ ng tròn là nh c a đ ng tròn đã cho quaườ ả ủ ườ
phép quay tâm O góc quay
0
90
, -.
0
90
Câu 36:
D ng nh c a hình vuông ự ả ủ ABCD qua phép
d i hình có đ c b ng cách th c hi n liênờ ượ ằ ự ệ
ti p phép đ i x ng tâm ế ố ứ A và phép quay tâm A
góc quay
0
90
.
Câu 37:
Trong h tr c t a đ ệ ụ ọ ộ Oxy, cho đ ng th ngườ ẳ
(d): 3x + y – 3 = 0 .
Tìm ph ng trình đ ng th ng ươ ườ ẳ (d’) là nhả
c a ủ(d) qua phép d i hình có đ c b ng cáchờ ượ ằ
th c hi n liên ti p phép đ i x ng tr c ự ệ ế ố ứ ụ Ox và
phép t nh ti n theo vec t ị ế ơ
( )
2, 3v
= −
r
.
Câu 38:
Cho tam giác ABC vuông t i ạA, G là tr ngọ
tâm tam giác. Tìm nh c a tam giác ả ủ ABC qua
phép v t :ị ự
a/Tâm G, t s ỉ ố
1
2
b/ Tâm G, t s 2ỉ ố
c/Tâm A, t s - 2ỉ ố
Câu 39:
Cho tam giác ABC . D ng nh c a nó có đ cự ả ủ ượ
b ng cách th c hi n liên ti p phép v t tâm ằ ự ệ ế ị ự A tỉ
s 2 và phép đ i x ng tâm ố ố ứ B.
Câu 40:
Trong m t ph ng ặ ẳ Oxy, cho đi m ểI(1,2) và
đ ng tròn tâm ườ I, bán kính 2. Vi t ph ng trìnhế ươ
đ ng tròn là nh c a đ ng tròn trên qua phépườ ả ủ ườ
đ ng d ng có đ c b ng cách th c hi n liênồ ạ ượ ằ ự ệ
ti p :ế
a/Phép quay tâm O, góc
0
45
và phép v t tâmị ự
O, t s ỉ ố 2.
b/ Phép đ i x ng tr c ố ứ ụ Oy và phép v t tâmị ự
O. t s ỉ ố
2
.
c/ Phép đ i x ng tâm ố ứ O và phép v t tâm ị ự O.
t s -2ỉ ố
Câu 4 1:
Trong m t ph ng t a đ Oxy, cho đi m ặ ẳ ọ ộ ể A(1, -3)
và đ ng th ng d có ph ng trình : ườ ẳ ươ 2x + y – 3
= 0, đ ng tròn ườ (C) có ph ng trình :ươ
2 2
4 6 3 0x y x y+ − + − =
.
a. Tìm t a đ đi m ọ ộ ể A’ và ph ng trình ươ d’ l nầ
l tượ là nh c a ả ủ A và d qua phép đ i x ng tr cố ứ ụ
Ox
b. Vi t ph ng trình đ ng tròn ế ươ ườ
( )
'C
là nhả
c a ủ(C) qua phép đ i x ng tâm ố ứ A
3
