Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
115
PHƯƠNG PHÁP PHÂN LOẠI DỮ LIỆU BẤT CÂN BẰNG
DỰA TRÊN TIỀN XỬ LÝ DỮ LIỆU VÀ SVM
Nguyễn Mạnh Hiển
Đại học Thủy lợi, email: hiennm@tlu.edu.vn
1. GIỚI THIỆU
Các thuật toán học máy chuẩn thường
không đạt được hiệu suất cao trên các tập dữ
liệu bất cân bằng, trong đó lớp dương (thiểu
số) có kích thước rất nhỏ so với lớp âm (đa
số). Bài báo đề xuất một phương pháp mới
cho phép phân loại hiệu quả các tập dữ liệu
bất cân bằng. Phương pháp này phân cụm lớp
đa số dùng thuật toán k-means và lấy mẫu lên
lớp thiểu số dùng kỹ thuật SMOTE. Bằng
cách coi mỗi cụm dữ liệu của lớp đa số như
một lớp mới, chúng tôi biến đổi tập huấn
luyện hai lớp bất cân bằng ban đầu thành một
tập huấn luyện đa lớp cân bằng hơn. Sau đó,
chúng tôi huấn luyện các bộ phân loại SVM
trên tập huấn luyện đa lớp thu được. Kết quả
thực nghiệm cho thấy phương pháp đề xuất
có hiệu suất phân loại đo bằng g-mean cao
hơn các phương pháp khác.
2. VẤN ĐỀ BẤT CÂN BẰNG DỮ LIỆU
Vấn đề phân loại dữ liệu bất cân bằng đã thu
hút được sự chú ý của nhiều nhà nghiên cứu kể
từ đầu những năm 2000 [7]. Các tập dữ liệu bất
cân bằng xuất hiện phổ biến trong nhiều ứng
dụng, như phát hiện giao dịch thẻ tín dụng gian
lận [2], phát hiện vết dầu loang trong ảnh vệ
tinh [9] và phân loại văn bản [6]. Mặc dù vậy,
các thuật toán học chuẩn thường không đạt
được hiệu suất mong muốn khi phân loại dữ
liệu bất cân bằng. Xét ví dụ với một tập huấn
luyện gồm 1% dữ liệu thuộc về lớp dương và
99% dữ liệu còn lại thuộc về lớp âm. Một thuật
toán học tầm thường có thể đạt được độ chính
xác 99% trên tập dữ liệu này bằng cách xác
định tất cả các mẫu dữ liệu thuộc về lớp âm.
Tuy nhiên, thuật toán này không có giá trị sử
dụng vì nó không nhận ra được bất cứ mẫu nào
của lớp dương. Nguyên nhân của vấn đề này là
các thuật toán học chuẩn chỉ tập trung tối ưu
hóa độ chính xác tổng thể trên toàn bộ tập huấn
luyện, do đó chúng ít quan tâm đến lớp thiểu
số. Vì độ chính xác tổng thể không thể chỉ ra
hiệu suất phân loại tốt hay kém trên lớp thiểu
số, bài báo này sẽ dùng một độ đo hiệu suất
phù hợp hơn gọi là g-mean (xem ở phần sau).
Nhiều phương pháp đã được đề xuất để giải
quyết vấn đề bất cân bằng dữ liệu. Một số
phương pháp thay đổi các thuật toán học chuẩn
để chúng làm việc tốt hơn trên dữ liệu bất cân
bằng, như căn chỉnh đường ranh giới quyết
định của SVM [11]. Những nghiên cứu khác
thực hiện tái cân bằng tập huấn luyện dùng các
kỹ thuật lấy mẫu [8], bao gồm lấy mẫu lên lớp
thiểu số và lấy mẫu xuống lớp đa số.
3. PHƯƠNG PHÁP ĐỀ XUẤT
Trong một tập huấn luyện bất cân bằng,
lớp đa số có kích thước lớn và có thể kèm
theo cả cấu trúc dữ liệu phức tạp. Chúng tôi
dùng thuật toán k-means để chia lớp đa số
thành các cụm nhỏ hơn, qua đó làm giảm
mức độ bất cân bằng lớp cũng như làm giảm
độ phức tạp cấu trúc của lớp đa số. Các bước
chính trong thuật toán đề xuất như sau:
Bước 1: Ước lượng số cụm tối ưu k của
lớp đa số dùng chỉ số DB (Davies-
Bouldin) [10].
Bước 2: Phân chia lớp đa số thành k cụm
dùng thuật toán k-means.
Bước 3: Lấy mẫu lên lớp thiểu số dùng kỹ
thuật SMOTE [4] cho đến khi lớp thiểu số
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
116
đạt kích thước trung bình của các cụm dữ
liệu trong lớp đa số.
Bước 4: Biến đổi tập huấn luyện hai lớp
ban đầu thành tập huấn luyện đa lớp, trong
đó mỗi cụm đa số trở thành một lớp mới.
Bước 5: Huấn luyện các bộ phân loại
SVM trên tập huấn luyện đa lớp mới theo
kiểu “một đấu một”, tức là huấn luyện một
SVM riêng biệt cho mỗi cặp lớp.
Bước 6: Dự đoán nhãn lớp của các mẫu
kiểm thử dùng kỹ thuật bỏ phiếu đa số.
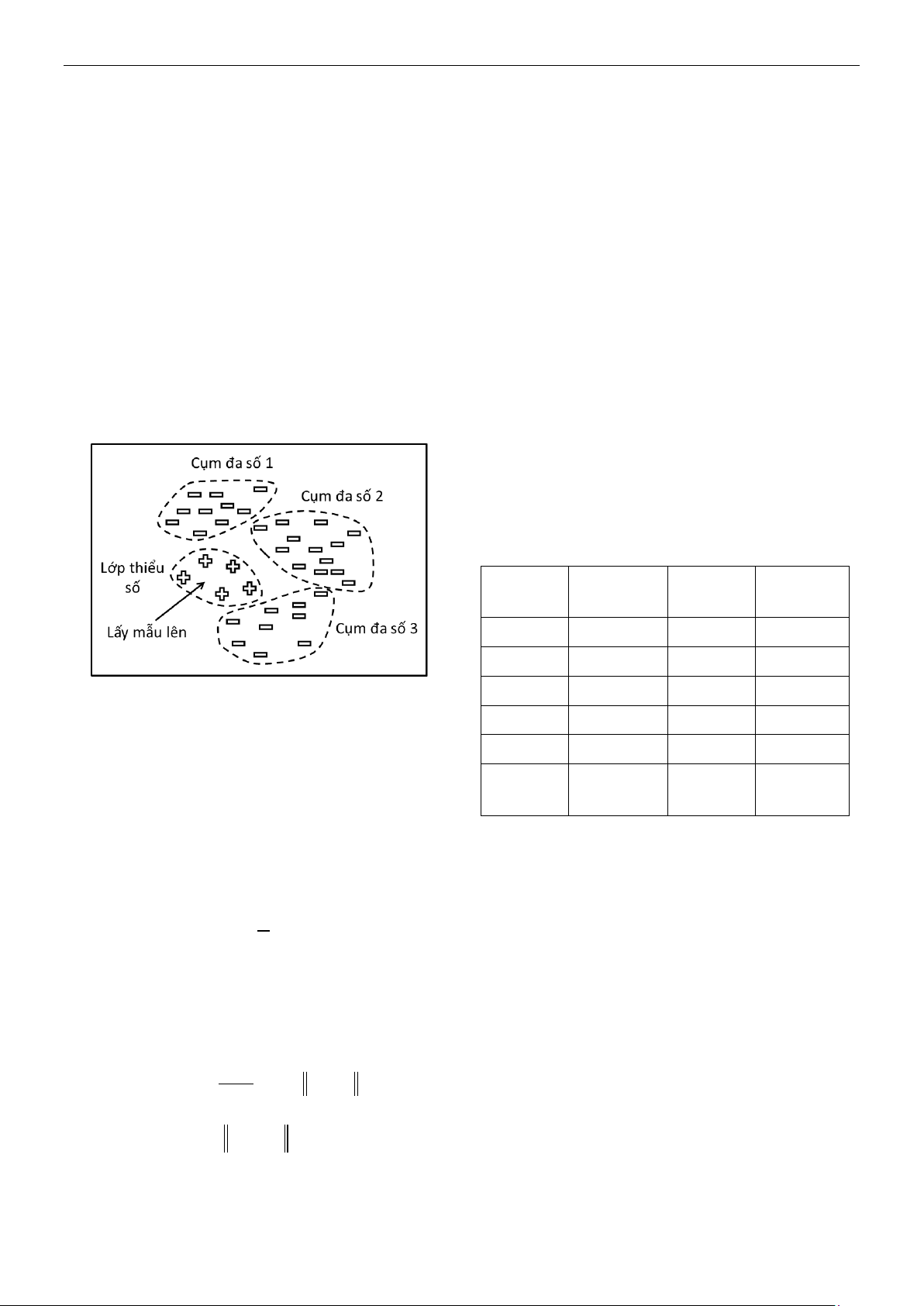
Hình 1 minh họa ý tưởng của phương pháp
đề xuất với ba cụm dữ liệu của lớp đa số và
một lớp thiểu số được lấy mẫu lên.
Hình 1. Minh họa phương pháp đề xuất
Trong bước 1 của thuật toán đề xuất, chỉ
số DB cho phép đánh giá chất lượng phân
cụm dữ liệu; chất lượng phân cụm tốt nếu độ
phân tán dữ liệu bên trong mỗi cụm nhỏ đồng
thời khoảng cách giữa các cụm lớn. Gọi Ci là
cụm thứ i và zi là véc-tơ trung bình của nó.
Khi đó, chỉ số DB được tính như sau:
k
i1
1
DB x
k
trong đó Sj và Sj là độ phân tán dữ liệu trong
các cụm Ci và Cj, còn dịj là khoảng cách giữa
các cụm Ci và Cj, và được tính như sau:
k
ii
i x Ci
ij i j
1
S x z
|C |
d z z
Trong bước 3 của thuật toán đề xuất, kỹ
thuật SMOTE sinh ra các mẫu nhân tạo để bổ
sung vào lớp thiểu số. Các mẫu nhân tạo
được sinh ngẫu nhiên trên các đoạn thẳng nối
một mẫu dữ liệu thiểu số với các láng giềng
gần nhất của (trong cùng lớp thiểu số).
4. THỰC NGHIỆM
Chúng tôi thực hiện các thí nghiệm đánh
giá hiệu suất phân loại của phương pháp đề
xuất trên sáu tập dữ liệu UCI [5]. Các tập dữ
liệu này có số lớp biến thiên từ 2 đến 28.
Chúng tôi đã chọn một lớp làm lớp thiểu số
và ghép tất cả các lớp còn lại thành lớp đa số.
Lớp thiểu số được chọn là 0 cho tập dữ liệu
Spect (chẩn đoán bệnh tim), 7 cho Glass (xác
định loại kính), 0 cho Vowel (nhận dạng
nguyên âm), 5 cho Yeast (định vị protein), 5
cho Abalone (dự đoán tuổi bào ngư) và 4 cho
Page-blocks (phân loại khối trang). Tóm tắt
của sáu tập dữ liệu này có trong Bảng 1.
Bảng 1. Các tập dữ liệu bất cân bằng
Tập dữ
liệu
Số thuộc
tính
Số mẫu
dữ liệu
Tỉ số bất
cân bằng
Spect
22
267
4
Glass
9
214
6
Vowel
10
990
10
Yeast
8
1484
28
Abalone
8
4177
35
Page-
blocks
10
5473
61
Các thuộc tính trong các tập dữ liệu được
chuẩn hóa tuyến tính về khoảng [-1; 1]. Mỗi
tập dữ liệu được chia ngẫu nhiên thành tập
huấn luyện và tập kiểm thử theo tỉ lệ 1:1 sao
cho giữ nguyên tỉ số bất cân bằng lớp.
Chúng tôi so sánh phương pháp đề xuất
với ba phương pháp sau đây:
SVM: Huấn luyện SVM chuẩn trên tập
huấn luyện bất cân bằng.
CS-SVM (Cost-Sensitive SVM) [1]: Định
trọng số các mẫu đa số bằng 1 và các mẫu
thiểu số bằng tỉ số bất cân bằng lớp.
SMOTE: Dùng SMOTE với tỉ lệ lấy mẫu
khác nhau tùy theo tỉ số bất cân bằng lớp;
cụ thể là 200% cho Spect, 400% cho
Glass, 500% cho Vowel và 1000% cho ba
tập dữ liệu còn lại. Tỉ lệ lấy mẫu N% có

Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
117
nghĩa là sinh ra lượng mẫu nhân tạo bằng
N% lần lớp thiểu số ban đầu.
Đối với thuật toán k-means trong phương
pháp đề xuất, chúng tôi thiết lập số bước lặp
tối đa của nó bằng 100. Thuật toán k-means
được lặp lại 10 lần với mỗi giá trị của k trong
khoảng từ 2 đến
n
, với n là là kích thước
của lớp đa số, để tìm ra kết quả phân cụm tốt
nhất ứng với chỉ số DB nhỏ nhất [10].
Đối với việc huấn luyện SVM, chúng tôi
dùng thư viện LIBSVM [3] với các tham số
ngầm định. Để giảm ảnh hưởng của yếu tố
ngẫu nhiên khi phân chia và lấy mẫu dữ liệu,
chúng tôi lặp lại các thí nghiệm mười lần và
tính hiệu suất trung bình dùng độ đo g-mean:
g-mean:
acc acc
trong đó acc+ và acc là độ chính xác phân
loại trên các lớp thiểu số và đa số.
Chúng tôi báo cáo kết quả thí nghiệm
trong Bảng 2, trong đó giá trị g-mean tốt
nhất cho mỗi tập dữ liệu được viết bằng chữ
in đậm. Kết quả cho thấy phương pháp đề
xuất có hiệu suất phân loại tốt nhất trên năm
tập dữ liệu, chỉ kém phương pháp SMOTE
trên một tập dữ liệu còn lại (Abalone)
nhưng với sai khác không lớn, chỉ 0,5 điểm
phần trăm.
Bảng 2. Hiệu suất phân loại (%) đo bằng
g-mean trên các tập dữ liệu bất cân bằng
Tập dữ
liệu
SVM
CS-
SVM
SMOTE
PP đề
xuất
Spect
61,0
62,5
65,6
71,4
Glass
88,4
90,1
86,5
91,0
Vowel
70,3
73,6
42,2
87,7
Yeast
17,5
33,2
57,8
65,5
Abalone
1,3
3,2
62,9
62,4
Page-
blocks
90,7
89,6
91,2
91,9
5. KẾT LUẬN
Bài báo đã giới thiệu một phương pháp
phân loại dữ liệu bất cân bằng mới. Phương
pháp này phân cụm lớp đa số và lấy mẫu lên
lớp thiểu số để tạo ra tập huấn luyện mới cân
bằng hơn. Kết quả thực nghiệm cho thấy
phương pháp đề xuất có hiệu suất phân loại
cao hơn các phương pháp khác.
6. TÀI LIỆU THAM KHẢO
[1] R. Akbani, S. Kwek, and N. Japkowicz
(2004) “Applying support vector machines
to imbalanced datasets,” ECML, pp. 39-50.
[2] P. Chan and S. Stolfo (1998) “Toward
scalable learning with non-uniform class
and cost distributions: A case study in credit
card fraud detection,” KDD, pp. 164-168.
[3] C. Chang and C. Lin (2011) “LIBSVM: A
library for support vector machines,” ACM
TIST, vol. 2, no. 3, pp. 27:1-27:27.
[4] N. Chawla, K. Bowyer, L. Hall, and W.
Kegelmeyer (2002) “SMOTE: Synthetic
minority over-sampling technique,” JAIR,
vol. 16, pp. 321-357.
[5] A. Frank and A. Asuncion (2010) “UCI
machine learning repository.” Available at
http://archive.ics.uci.edu/ml.
[6] E. Frank and R. Bouckaert (2006) “Naive
Bayes for text classification with
unbalanced classes,” PKDD, pp. 503-510.
[7] H. He and E. Garcia (2009) “Learning from
imbalanced data,” TKDE, vol. 21, no. 9, pp.
1263-1284.
[8] J. Hulse, T. Khoshgoftaar, and A.
Napolitano (2007) “Experimental
perspectives on learning from imbalanced
data,” ICML, pp. 935-942.
[9] M. Kubat, R. Holte, and S. Matwin (1998)
“Machine learning for the detection of oil
spills in satellite radar images,” MLJ, vol.
30, no. 2-3, pp. 195-215.
[10] U. Maulik and S. Bandyopadhyay (2002)
“Performance evaluation of some clustering
algorithms and validity indices,” TPAMI,
vol. 24, no. 12, pp. 1650-1654.
[11] G. Wu and E. Chang (2005) “KBA: Kernel
boundary alignment considering
imbalanced data distribution,” TKDE, vol.
17, no. 6, pp. 786-795.