Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
80
PHƯƠNG PHÁP XÂY DỰNG TRI THỨC TỪ TẬP DỮ LIỆU
Nguyễn Văn Thẩm1, Nguyễn Đỗ Kiều Loan2
1Trường Đại học Thủy lợi, email: thamnv@tlu.edu.vn
2Học viện Tài chính
1. GIỚI THIỆU CHUNG
Trong quá trình phát triển hệ thống dựa
trên tri thức, việc biểu diễn tri thức là giai
đoạn đầu tiên và rất quan trọng. Lựa chọn
một mô hình để biểu diễn tri thức tuỳ thuộc
vào nhiều yếu tố như loại tri thức, công cụ
hiện có,... Tri thức có thể được biểu diễn
bằng luật và suy diễn logic, mạng ngữ nghĩa,
khung, mô hình dựa trên logic mờ, hàm xác
suất cơ bản (Basic Probability Assignment-
BPA),... Tri thức biểu diễn bằng BPA có hạn
chế các BPA phải thoả mãn
0m . Tuy
nhiên trong thực tế, có thể tồn tại tri thức mà
0m , các tri thức dạng này được gọi là
GBPA (Generalized BPA).
Bài báo đề xuất thuật toán xây dựng các
tri thức từ các nguồn dữ liệu, trong đó các cơ
sở tri thức được biểu diễn bằng GBPA.
2. NỘI DUNG
2.1. Một số khái niệm
Đặt
11
, ,..., n
FEE E là một khung phân
biệt gồm một tập hữu hạn không rỗng chứa n
biến cố loại trừ lẫn nhau. Đặt h = 2n. Tập lũy
thừa (Power Set) của F là một tập gồm h
phần tử
1121
, ,..., , ,..., ...
nn
FEEEEEE .
Định nghĩa 1. [1] Hàm
0,1
:mF
được gọi là GBPA nếu thỏa mãn tính chất sau:
1
F
m
Cho
1,..., m
Cc c và
1,..., n
A
aa lần lượt
là các cụm và các thuộc tính của một tập dữ
liệu. Gọi
ij nm
M
là ma trận trung bình
mẫu của tập dữ liệu, trong đó ij
1
1j
i
c
kj
k
j
x
c
với xk,j là giá trị mẫu thử k tương ứng với
thuộc tính ai và cụm cj. Gọi
ij nm
D
là
ma trận độ lệch chuẩn của tập dữ liệu, trong
đó
2
ij ij
1
1
1
j
i
c
kj
k
j
x
c
Gọi
ij nm
Ll
và
ij nm
Uu
là ma trận cận
dưới và ma trận cận trên của tập dữ liệu, trong
đó:
là tham số mở rộng,
ij i
kj ij
lMinx
,
ij i
kj ij
u Max x
.
Định nghĩa 2. [2] Cho
1,..., m
Cc c và
1,..., n
A
aa lần lượt là các cụm và các
thuộc tính của tâp dữ liệu. Hàm thành viên
tam giác (triangular membership function)
biểu diễn đường tam giác mờ của m cụm
trong n thuộc tính, được định nghĩa như sau:
0
-
-
0
ij
ij
ij ij
ij ij
ij
ij ij
ij ij
ij
xl
xl lx
l
fx ux xu
u
x
2.2. Thuật toán xây dựng tri thức
Bài báo đề xuất thuật toán tìm tri thức từ
một tập dữ liệu [2, 3] như sau:
(1) Đầu vào: Một tập dữ liệu gồm m cụm
1,..., m
Cc cvà n thuộc tính
1,..., n
A
aa.
(2) Đầu ra: Tri thức của thuộc tính ai A
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
81
(3) Phạm vi bài toán: Tri thức được biểu
diễn bằng GBPA
(4) Tiến trình:
Bước 1: Tính các ma trận trung bình mẫu,
độ lệch chuẩn, ma trận cận dưới và ma trận
cận trên của tập dữ liệu.
Bước 2: Xác định các đường tam giác mờ
của m cụm trong n thuộc tính theo Định
nghĩa 2.
Bước 3: Với i
aA
1,in, thêm mẫu thử
xi =
vào mô hình sao cho xi giao với đường
tam giác mờ của m cụm:
- Tìm các giao điểm và sắp xếp theo chiều
giảm dần sao cho 12
1 ... 0
m
.
- Tính
1
m
i
i
Bước 4: 1,km
Nếu 1 thì
1
( ,..., )
kk
mc c
, ()1m
Nếu 1 thì
1
( ,..., ) k
k
mc c
, () 0m
2.3. Ví dụ tính toán và thảo luận
Tập dữ liệu Iris được lấy từ kho lưu trữ UCI
(http://archive.ics.uci.edu/ml/datasets/Iris). Bộ
dữ liệu Iris chứa ba cụm: Setosa (Se),
Versicolour (Ve) và Virginica (Vi). Mỗi cụm
chứa 50 mẫu và có bốn thuộc tính: chiều dài
đài hoa (SL-sepal length), chiều rộng đài hoa
(SW-sepal width), chiều dài cánh hoa (PL-
petal length) và chiều rộng cánh hoa (PW-
petal width). Do đó, ta có
,,CSeVeVi và
,,,
A
SL SW PL PW
Tiến trình thực hiện thuật toán:
Bước 1: Xây dựng các ma trận
5.01 5.94 6.59
3.43 2.77 2.97
1.46 4.26 5.55
0.25 1.33 2.03
M
,
0.35 0.52 0.64
0.38 0.31 0.32
0.17 0.47 0.55
0.11 0.20 0.27
D
Cho 0.3
, ta có:
4.19 4.75 4.71
2.19 1.91 2.10
0.95 2.86 4.33
0.07 0.94 1.32
L
,
5.91 7.05 8.09
4.51 3.49 3.90
1.95 5.24 7.07
0.63 1.86 2.58
U
Bước 2: Xác định các đường tam giác mờ
của 3 cụm {Se, Ve, Vi} và trong 4 thuộc tính
{SL, SW, PL, PW}. Ví dụ, đường đường tam
giác mờ của 3 cụm với thuộc tính SL được
chỉ ra trong Hình 1.
Bước 3: Với mỗi thuộc tính, tìm các giao
điểm của mẫu thử với tất cả đường tam giác
mờ của m cụm.
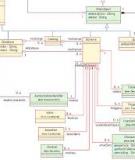
- Xét thuộc tính SL với mẫu thử x1 = 5.6 trên
cả 3 cụm {Se, Ve, Vi}. Giao điểm của x1 = 5.6
với mô hình đường tam giác mờ của 3 cụm
được chỉ ra trong Hình 1.
Hình 1. Mô hình đường tam giác mờ theo SL
+ Xét đường tam giác của cụm Se,
phương trình đường thẳng đi qua hai điểm
11,1 5.01,1A
và
11,0 5.91,0Bu
là 1.11 6.56yx
. Giao của đường thẳng
1.11 6.56yx
và 15.6x là
0.34ySe.
+ Xét đường tam giác của cụm Ve,
phương trình đường thẳng đi qua hai điểm
12 ,0 4.75,0Al và
12 ,1 5.94,1B
là 0.84 3.98yx
. Giao của đường thẳng
0.84 3.98yx
và 15.6x là
0.72yVe .
+ Xét đường tam giác của cụm Vi,
phương trình đường thẳng đi qua hai điểm
13,0 4.71,0Al và
13,1 6.59,1B
là 0.53 2.51yx
. Giao của đường thẳng
0.53 2.51yx
và 15.6x là
0.47yVi .
Ta có: 10.72
, 20.47
, 30.34
.
123
1.53
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
82
Vì 1.53 1 nên
0.72 0.47
1.53
mVe
,
, 0.31mVeVi ,
, , 0.22mVeViSe
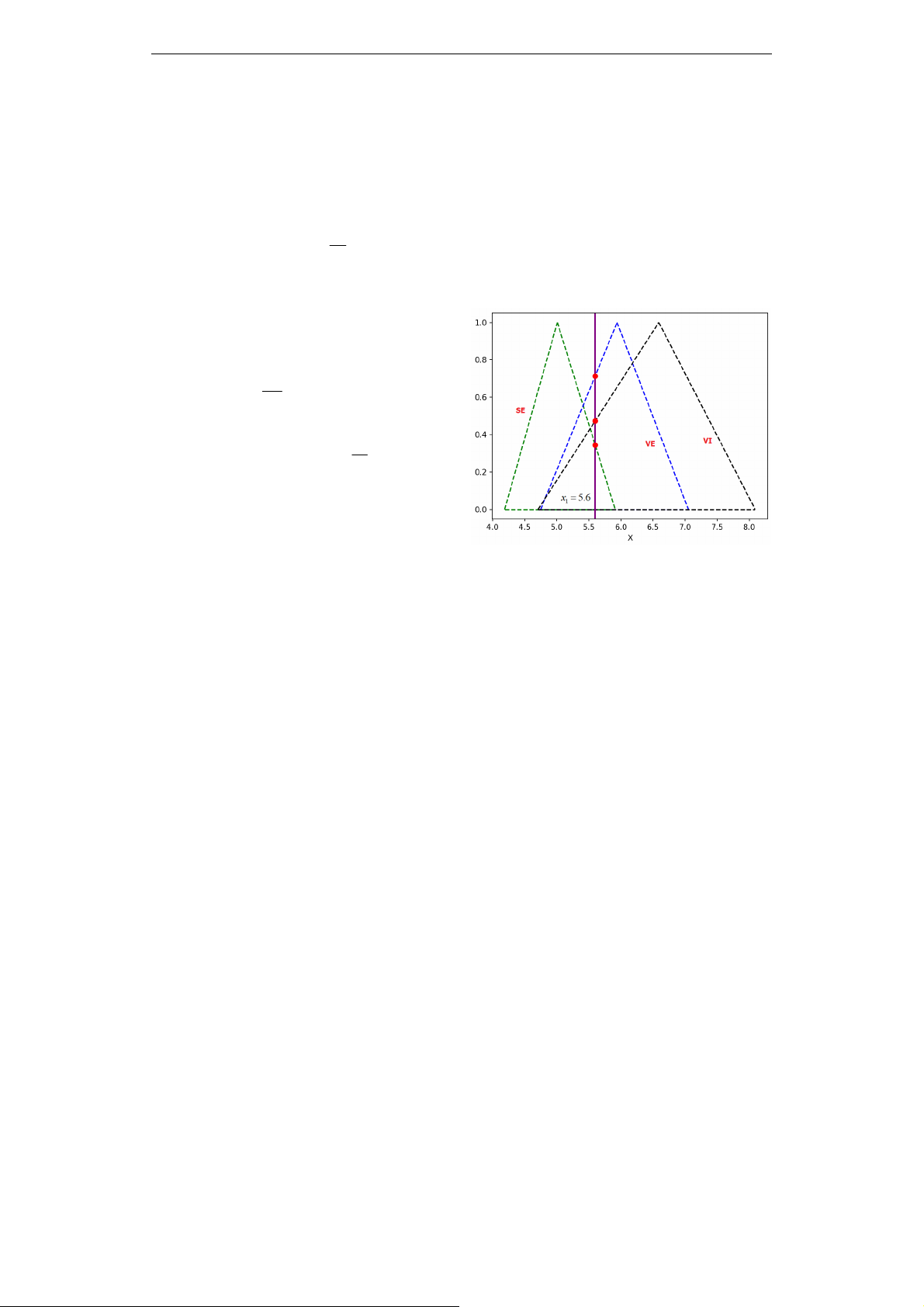
- Xét thuộc tính
P
Wvới mẫu thử 31.6x
trên cả 3 cụm
,,Se Ve Vi . Giao điểm của
41.6x với mô hình đường tam giác mờ của
3 cụm được chỉ ra trong Hình 2.
+ Xét đường tam giác của cụm Se,
phương trình đường thẳng đi qua hai điểm
41,0 0.07,0Al và
41,0 0.25,0B
là 5.63 0.39yx. Giao của đường thẳng
5.63 0.39yx
và 41.6x là
8.62 1ySe
.
Hình 2. Mô hình đường tam giác mờ theo PW
+ Xét đường tam giác của cụm Ve,
phương trình đường thẳng đi qua hai điểm
42 ,1 1.33,1A
và
42 ,0 1.86,0Bu
là 1.88 3.49yx . Giao của đường thẳng
1.88 3.49yx và 41.6x là
0.49yVe .
+ Xét đường tam giác của cụm Vi,
phương trình đường thẳng đi qua hai điểm
43,0 1.32,0Al và
43,1 2.03,1B
là 1.11 5.56yx. Giao của đường thẳng
1.11 5.56yx và 41.6x là
0.4yVi .
Ta có: 10.49
, 20.4
, 30
.
123
0.88
Vì 0.88 1 nên
0.49mVe ,
, 0.4mVeVi ,
,, 0mVeViSe
,
1 0.88 0.12m
Bảng 1 chỉ ra cơ sở tri thức của các thuộc
tính
,,,SL SW PL PW được biểu diễn bằng các
GBPA. Kết quả thu được cho thấy các GBPA
của các thuộc tính đều thoả mãn
tính
1
m
trong Định nghĩa 1.
Bảng 1. Cơ sở tri thức của các thuộc tính
GBPA SL SW PL PW
{Ve} 0.47 0.49 0.45 0.49
{Vi} 0 0 0 0
{Se} 0 0 0 0
{Ve,Vi} 0.31 0.33 0.38 0.40
{Ve,Se} 0 0 0 0
{Vi,Se} 0 0 0 0
{Ve,Vi,Se} 0.22 0.18 0 0
0 0 0.17 0.12
3. KẾT LUẬN
Bài báo này đã đề xuất một thuật toán để
tiến hành tìm tri thức của tập dữ liệu cho trước,
trong đó các tri thức cần tìm sẽ được biểu diễn
bằng các GBPA. Tri thức được biểu diễn bằng
các GBPA khắc phục được hạn chế khi mà tri
thức được biểu diễn bằng các BPA không phù
hợp với tri thức tồn tại
0m
. Các tri thức
của từng thuộc tính có thể được đem tính hợp
với nhau bằng một phương pháp tích hợp tri
thức nào đó để có được một tri thức chung
biểu diễn cho tri thức của từng cụm dữ liệu.
Kết quả của bài báo là cơ sở để trong tương lai
tác giả xem xét sẽ xem xét vấn đề ứng dụng
trong các bài toán phân cụm và phân lớp.
4. TÀI LIỆU THAM KHẢO
[1] Deng, Y. 2015. Generalized evidence
theory. Appl Intell 43, 530-543.
[2] Zhang, Jingfei & Deng, Yong. 2017. A
method to determine basic probability
assignment in the open world and its
application in data fusion and classification.
Applied Intelligence. 46.
[3] Fan, Y., Ma, T. & Xiao, F. 2021. An
improved approach to generate generalized
basic probability assignment based on fuzzy
sets in the open world and its application in
multi-source information fusion. Appl Intell
51, 3718-3735.