( Hình 1 )
B
O
A
v
B
v
A
x
.
y
.
B
.
O
A
x
y
.
.
.
A
1
B
1
d
Tài li u b i d ng HSG – Môn V t lý 9ệ ồ ưỡ ậ
CÁC BÀI TOÁN V CHUY N Đ NG C A CÁC V TỀ Ể Ộ Ủ Ậ
A/ Các bài toán v chuy n đ ng c a v t và h v tề ể ộ ủ ậ ệ ậ
1/ H v t g m các v t chuy n đ ng v i v n t c cùng ph ngệ ậ ồ ậ ể ộ ớ ậ ố ươ :
Ph ng pháp: s d ng tính t ng đ i c a chuy n đ ng và công th c c ng v n t c. trongươ ử ụ ươ ố ủ ể ộ ứ ộ ậ ố
tr ng h p các v t chuy n đ ng cùng chi u so v i v t m c thì nên ch n v t có v n t c nh h nườ ợ ậ ể ộ ề ớ ậ ố ọ ậ ậ ố ỏ ơ
làm m c m i đ xét các chuy n đ ng.ố ớ ể ể ộ
Bài toán:
Trên m t đ ng đua th ng, hai bên l đ ng có hai hàng d c các v n đ ng viên chuy n đ ngộ ườ ẳ ề ườ ọ ậ ộ ể ộ
theo cùng m t h ng: m t hàng là các v n đ ng viên ch y vi t dã và hàng kia là các v n đ ngộ ướ ộ ậ ộ ạ ệ ậ ộ
viên đua xe đ p. Bi t r ng các v n đ ng viên vi t dã ch y đ u v i v n t c vạ ế ằ ậ ộ ệ ạ ề ớ ậ ố 1 = 20km/h và
kho ng cách đ u gi a hai ng i li n k nhau trong hàng là lả ề ữ ườ ề ề 1 = 20m; nh ng con s t ng ngữ ố ươ ứ
đ i v i hàng các v n đ ng viên đua xe đ p là vố ớ ậ ộ ạ 2 = 40km/h và l2 = 30m. H i m t ng i quan sátỏ ộ ườ
c n ph i chuy n đ ng trên đ ng v i v n t c vầ ả ể ộ ườ ớ ậ ố 3 b ng bao nhiêu đ m i l n khi m t v n đ ngằ ể ỗ ầ ộ ậ ộ
viên đua xe đ p đu i k p anh ta thì chính lúc đó anh ta l i đu i k p m t v n đ ng viên ch y vi tạ ổ ị ạ ổ ị ộ ậ ộ ạ ệ
dã ti p theo?ế
Gi i: Coi v n đ ng viên vi t dã là đ ng yên so v i ng i quan sát và v n đ ng viên đua xe đ p.ả ậ ộ ệ ứ ớ ườ ậ ộ ạ
V n t c c a v n đ ng viên xe đ p so v i v n đ ng viên vi t dã là: Vậ ố ủ ậ ộ ạ ớ ậ ộ ệ x = v2 – v1 = 20 km/h.
V n t c c a ng i quan sát so v i v n đ ng viên vi t dã là: Vậ ố ủ ườ ớ ậ ộ ệ n = v3 – v1 = v3 – 20
Gi s t i th i đi m tính m c th i gian thì h ngang nhau.ả ử ạ ờ ể ố ờ ọ
Th i gian c n thi t đ ng i quan sát đu i k p v n đ ng viên vi t dã ti p theo là: ờ ầ ế ể ườ ổ ị ậ ộ ệ ế
n
V
l
t1
1=
Th i gian c n thi t đ VĐV xe đ p phía sau đu i k p VĐV vi t dã nói trên là: ờ ầ ế ể ạ ổ ị ệ
X
V
ll
t
21
2
+
=
Đ h l i ngang hàng thì tể ọ ạ 1 = t2. hay:
X
V
ll
v
l21
3
1
20
+
=
−
Thay s tìm đ c: vố ượ 3 = 28 km/h
2/ H v t g m các v t chuy n đ ng v i v n t c khác ph ngệ ậ ồ ậ ể ộ ớ ậ ố ươ
Ph ng pháp: S d ng công th c c ng v n t c và tính t ng đ iươ ử ụ ứ ộ ậ ố ươ ố
c a chuy n đ ng:ủ ể ộ
Bài toán:
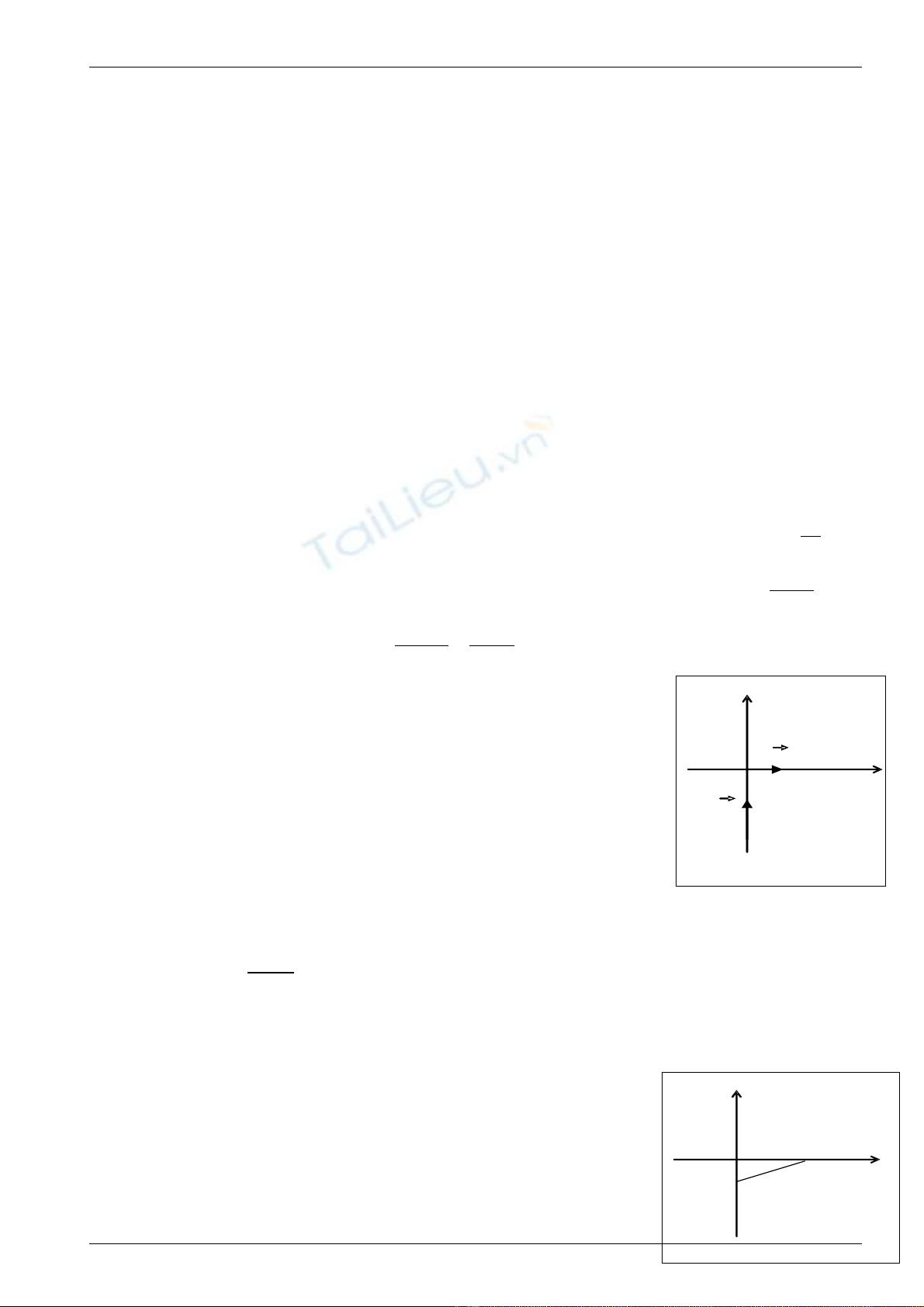
Trong h t a đ xoy ( hình 1), có hai v t nh A và B ệ ọ ộ ậ ỏ
chuy n đ ng th ng đ u. Lúc b t đ u chuy n đ ng, v t A cách ể ộ ẳ ề ắ ầ ể ộ ậ
v t B m t đo n l = 100m. ậ ộ ạ
Bi t v n t c c a v t A là vế ậ ố ủ ậ A = 10m/s theo h ng ox, ướ
v n t c c a v t B là vậ ố ủ ậ B = 15m/s theo h ng oy.ướ
a) Sau th i gian bao lâu k t khi b t đ u chuy n đ ng, ờ ể ừ ắ ầ ể ộ
hai v t A và B l i cách nhau 100m.ậ ạ
b) Xác đ nh kho ng cách nh nh t gi a hai v t A và B.ị ả ỏ ấ ữ ậ
Gi i:ả
a/ Quãng đ ng A đi đ c trong t giây: AAườ ượ 1 = vAt
Quãng đ ng B đi đ c trong t giây: BBườ ượ 1 = vBt
Kho ng cách gi a A và B sau t giây: dả ữ 2 = (AA1)2 + (AB1)2
V i AAớ1 = VAt và BB1 = VBt
Nên: d2 = ( v2A + v2B )t2 – 2lvBt + l2 (*)
Thay s và bi n đ i ra bi u th c : 325tố ế ổ ể ứ 2 – 3000t = 0
Gi i ra đ c: t ả ượ
≈
9,23 s
b/ - Xét ph ng trình b c hai (ươ ậ *) v i bi n là t. Đ (*) cóớ ế ể
nghi m thìệ
1

Tài li u b i d ng HSG – Môn V t lý 9ệ ồ ưỡ ậ
0'
≥∆
t đó tìm đ c: ừ ượ
B
2
A
2
A
22
min
2
vv
vl
a4
)d( +
=
∆
−=
- Rút ra đ c dượ min =
B
2
A
2
A
vv
vl
+
- Thay s tính đ c dố ượ min
≈
55,47 m
3/ Chuy n đ ng l p:ể ộ ặ
Ph ng pháp: Có th s d ng m t trong hai ph ng pháp sau:ươ ể ử ụ ộ ươ
a) N u v t chuy n đ ng l p không thay đ i v n t c trên c quá trình chuy n đ ng thì sế ậ ể ộ ặ ổ ậ ố ả ể ộ ử
d ng tính t ng đ i c a chuy n đ ngụ ươ ố ủ ể ộ
b) N u v t tham gia chuy n đ ng l p có v n t c thay đ i trên các quãng đ ng thì s d ngế ậ ể ộ ặ ậ ố ổ ườ ử ụ
ph ng pháp t s quãng đ ng ho c tính t ng đ i c a chuy n đ ng. ươ ỷ ố ườ ặ ươ ố ủ ể ộ
Bài toán 1: Trên quãng đ ng dài 100 km có 2 xe 1 và 2 cùng xu t phát và chuy n đ ng g p nhauườ ấ ể ộ ặ
v i v n t c t ng ng là 30 km/h và 20 km/h. cùng lúc hai xe chuy n đ ng thì có m t con Ongớ ậ ố ươ ứ ể ộ ộ
b t đ u xu t phát t xe 1 bay t i xe 2, sau khi g p xe 2 nó quay l i và g p xe 1… và l i bay t iắ ầ ấ ừ ớ ặ ạ ặ ạ ớ
xe 2. Con Ong chuy n đ ng l p đi l p l i t i khi hai xe g p nhau. Bi t v n t c c a con ong làể ộ ặ ặ ạ ớ ặ ế ậ ố ủ
60Km/h. tính quãng đ ng Ông bay?.ườ
Gi i: Coi xe 2 đ ng yên so v i xe 1. thì v n t c c a xe 2 so v i xe 1 là Vả ứ ớ ậ ố ủ ớ 21 = V2 + V1 = 50 Km/h
Th i gian đ 2 xe g p nhau là: t = = = 2 hờ ể ặ
Vì th i gian Ong bay b ng th i gian hai xe chuy n đ ng. Nên quãng đ ng Ong bay là:ờ ằ ờ ể ộ ườ
So = Vo t = 60.2 = 120 Km
Bài toán 2: M t c u bé đi lên núi v i v n t c 1m/s. khi còn cách đ nh núi 100m c u bé th m tộ ậ ớ ậ ố ỉ ậ ả ộ
con chó và nó b t đ u ch y đi ch y l i gi a đ nh núi và c u bé. Con chó ch y lên đ nh núi v iắ ầ ạ ạ ạ ữ ỉ ậ ạ ỉ ớ
v n t c 3m/s và ch y l i phía c u bé v i v n t c 5m/s. tính quãng đ ng mà con chó đã ch y tậ ố ạ ạ ậ ớ ậ ố ườ ạ ừ
lúc đ c th ra t i khi c u bé lên t i đ nh núi?ượ ả ớ ậ ớ ỉ
Gi i:ả
V n t c c a c u bé là v, v n t c c a con chó khi ch y lên là vậ ố ủ ậ ậ ố ủ ạ 1 và khi ch y xu ng là vạ ố 2 . Gi sả ử
con chó g p c u bé t i m t đi m cách đ nh núi là s th i gian gi a hai l n g p nhau liên ti p là tặ ậ ạ ộ ể ỉ ờ ữ ầ ặ ế
Th i gian con chó ch y t ch g p c u bé t i đ nh núi là s/vờ ạ ừ ỗ ặ ậ ớ ỉ 1 th i gian con chó ch y t đ nh núiờ ạ ừ ỉ
t i ch g p c u bé l n ti p theo là (t-s/vớ ỗ ặ ậ ầ ế 1 ) và quãng đ ng mà con chó đã ch y trong th i gianườ ạ ờ
này là v2(t– s/v1) . Quãng đ ng mà c u bé đã đi trong th i gian t là vt nên: s = vt + vườ ậ ờ 2 (t – s/t1)
Hay t =
2
1
2
)1(
vv
v
v
s
+
+
Quãng đ ng con chó ch y c lên núi và xu ng núi trong th i gian t là:ườ ạ ả ố ờ
Sc = s+ v2(t – s/v1) thay giá tr c a t t trên ta đ c: Sị ủ ừ ượ c = s
)(
)(2
21
1221
vvv
vvvvv
+
−−
Quãng đ ng c u bé đã đi trong th i gian t là: Sườ ậ ờ b = s
)(
)(
21
21
vvv
vvv
+
+
. T đó ta đ c Sừ ượ c =
2
7
Sb = 350 m.
3/ Chuy n đ ng có v n t c thay đ i theo quy lu t:ể ộ ậ ố ổ ậ
Ph ng pháp: ươ
+ Xác đ nh quy lu t c a chuy n đ ng ị ậ ủ ể ộ
+ Tính t ng quãng đ ng chuy n đ ng. T ng này th ng là t ng c a m t dãy s .ổ ườ ể ộ ổ ườ ổ ủ ộ ố
+ Gi i ph ng trình nh n đ c v i s l n thay đ i v n t c là s nguyên.ả ươ ậ ượ ớ ố ầ ổ ậ ố ố
Bài toán 1: M t đ ng t xu t phát t A trên đ ng th ng h ng v B v i v n t c ban đ u Vộ ộ ử ấ ừ ườ ẳ ướ ề ớ ậ ố ầ 0
= 1 m/s, bi t r ng c sau 4 giây chuy n đ ng, v n t c l i tăng g p 3 l n và c chuy n đ ngế ằ ứ ể ộ ậ ố ạ ấ ầ ứ ể ộ
đ c 4 giây thì đ ng t ng ng chuy n đ ng trong 2 giây. trong khi chuy n đ ng thì đ ng t chượ ộ ử ừ ể ộ ể ộ ộ ử ỉ
chuy n đ ng th ng đ u. Sau bao lâu đ ng t đ n B bi t AB dài 6km?ể ộ ẳ ề ộ ử ế ế
Gi i: c 4 giây chuy n đ ng ta g i là m t nhóm chuy n đ ngả ứ ể ộ ọ ộ ể ộ
2

Tài li u b i d ng HSG – Môn V t lý 9ệ ồ ưỡ ậ
D th y v n t c c a đ ng t trong các n nhóm chuy n đ ng đ u tiên là: ễ ấ ậ ố ủ ộ ử ể ộ ầ
30 m/s; 31 m/s; 32 m/s …….., 3n-1 m/s ,……..,
Quãng đ ng t ng ng mà đ ng t đi đ c trong các nhóm th i gian t ng ng là: ườ ươ ứ ộ ử ượ ờ ươ ứ
4.30 m; 4.31 m; 4.32 m; …..; 4.3n-1 m;…….
Quãng đ ng đ ng t chuy n đ ng trong th i gian này là: Sườ ộ ử ể ộ ờ n = 4( 30 + 31 + 32 + ….+ 3n-1) (m)
Hay: Sn = 2(3n – 1) (m)
Ta có ph ng trình: 2(3ươ n -1) = 6000 ⇒ 3n = 3001.
Ta th y r ng 3ấ ằ 7 = 2187; 38 = 6561, nên ta ch n n = 7.ọ
Quãng đ ng đ ng t đi đ c trong 7 nhóm th i gian đ u tiên là: 2.2186 = 4372 (m)ườ ộ ử ượ ờ ầ
Quãng đ ng còn l i là: 6000 – 4372 = 1628 (m)ườ ạ
Trong quãng đ ng còn l i này đ ng t đi v i v n t c là ( v i n = 8): 3ườ ạ ộ ử ớ ậ ố ớ 7 = 2187 (m/s)
Th i gian đi h t quãng đ ng còn l i này là: ờ ế ườ ạ
)(74,0
2187
1628 s=
V y t ng th i gian chuy n đ ng c a đ ng t là: 7.4 + 0,74 = 28,74 (s)ậ ổ ờ ể ộ ủ ộ ử
Ngoài ra trong quá trình chuy n đ ng. đ ng t có ngh 7 l n ( không chuy n đ ng) m i l n nghể ộ ộ ử ỉ ầ ể ộ ỗ ầ ỉ
là 2 giây, nên th i gian c n đ đ ng t chuy n đ ng t A t i B là: 28,74 + 2.7 = 42,74 (giây).ờ ầ ể ộ ử ể ộ ừ ớ
Bài toán 2: M t v t chuy n đ ng xu ng d c nhanh d n. Quãng đ ng v t đi đ c trong giâyộ ậ ể ộ ố ố ầ ườ ậ ượ
th k là S = 4k - 2 (m). Trong đó S tính b ng mét, còn k = 1,2, … tính b ng giây.ứ ằ ằ
a/ Hãy tính quãng đ ng đi đ c sau n giây đ u tiên.ườ ượ ầ
b/ V đ th s ph thu c c a quãng đ ng đi đ c vào th i gian chuy n đ ng.ẽ ồ ị ự ụ ộ ủ ườ ượ ờ ể ộ
Gi i: a/ Quãng đ ng đi đ c trong n giây đ u tiên là: ả ườ ượ ầ
Sn = (4.1 – 2) + (4.2 – 2) + (4.3 – 2) +…….+ (4.n -2)
Sn = 4(1 + 2 + 3 + …… + n) – 2n
Sn = 2n(n + 1) – 2n = 2n2
b/ Đ th là ph n đ ng parabol Sồ ị ầ ườ n = 2n2 n m bên ph i tr c Sằ ả ụ n.
B/ Các bài toán v v n t c trung bình c a v t chuy n đ ngề ậ ố ủ ậ ể ộ .
Ph ng pháp: Trên quãng đ ng S đ c chia thành các quãng đ ng nh Sươ ườ ượ ườ ỏ 1; S2; …; Sn và th iờ
gian v t chuy n đ ng trên các quãng đ ng y t ng ng là tậ ể ộ ườ ấ ươ ứ 1; t2; ….; tn. thì v n t c trung bìnhậ ố
trên c quãng đ ng đ c tính theo công ả ườ ượ
th c: VứTB =
1 2
1 2
....
.....
n
n
s s s
t t t
+ + +
+ + +
Chú ý: V n t c trung bình khác v i trung bình c a các v n t c.ậ ố ớ ủ ậ ố
Bài toán 1: Hai b n Hoà và Bình b t đ u ch y thi trên m t quãng đ ng S. Bi t Hoà trên n aạ ắ ầ ạ ộ ườ ế ử
quãng đ ng đ u ch y v i v n t c không đ i vườ ầ ạ ớ ậ ố ổ 1 và trên n a quãng đ ng sau ch y v i v n t cử ườ ạ ớ ậ ố
không đ i vổ2(v2< v1). Còn Bình thì trong n a th i gian đ u ch y v i v n t c vử ờ ầ ạ ớ ậ ố 1 và trong n a th iử ờ
gian sau ch y v i v n t c vạ ớ ậ ố 2 .
Tính v n t c trung bình c a m i b n ?ậ ố ủ ỗ ạ
Gi i: ả
Xét chuy n đ ng c a Hoà A ể ộ ủ v1 M v2 B
Th i gian đi vờ1là t1 = =
Th i gian đi vờ2 là t2 = = . Th i gian t = tờ1+t2 = s( +)
v n t c trung bình vậ ố H = = (1)
Xét chuy n đ ng c a Bình Aể ộ ủ v1 M v2 B
s1 = v1t1 ; s2 = v2t2 mà t1= t2 = và s = s1 + s2 => s= ( v1+v2) => t=
v n t c trung bình vậ ố B = =
Bài toán 2:
M t ng i đi trên quãng đ ng S chia thành n ch ng không đ u nhau, chi u dài các ch ng đó l nộ ườ ườ ặ ề ề ặ ầ
l t là Sượ 1, S2, S3,......Sn.
3

Tài li u b i d ng HSG – Môn V t lý 9ệ ồ ưỡ ậ
Th i gian ng i đó đi trên các ch ng đ ng t ng ng là tờ ườ ặ ườ ươ ứ 1, t2 t3....tn . Tính v n t c trung bìnhậ ố
c a ng i đó trên toàn b qu ng đ ng S. Ch ng minh r ng:v n trung bình đó l n h n v n t củ ườ ộ ả ườ ứ ằ ậ ớ ơ ậ ố
bé nh t và nh h n v n t c l n nh t.ấ ỏ ơ ậ ố ớ ấ
Gi i:ả V n t c trung bình c a ng i đó trên quãng đ ng S là: Vậ ố ủ ườ ườ tb=
tttt
ssss
n
n
++++
+++
....
.....
321
321
G i Vọ1, V2 , V3 ....Vn là v n t c trên các ch ng đ ng t ng ng ta có:ậ ố ặ ườ ươ ứ
;
1
1
1
t
s
v
=
;
2
2
2
t
s
v
=
;
3
3
3
t
s
v
=
.......
;
t
s
v
n
n
n
=
gi s Vả ử kl n nh t và Vớ ấ i là bé nh t ( n ấ≥ k >i ≥ 1)ta ph i ch ng minh Vả ứ k > Vtb > Vi.Th t v y:ậ ậ
Vtb=
tttt
tvtvtvtv
n
nn
++++
+++
....
.....
321
332211
= vi
tttt
t
v
v
t
v
v
t
v
v
t
v
v
n
n
i
n
iii
++++
+++
....
.....
321
3
3
2
2
1
1
.Do
v
v
i
1
;
v
v
i
1
...
v
v
i
1
>1 nên
v
v
i
1
t1+
v
v
i
1
t2.+..
v
v
i
1
tn> t1 +t2+....tn → Vi< Vtb (1)
T ng t ta có Vươ ự tb=
tttt
tvtvtvtv
n
nn
++++
+++
....
.....
321
332211
= vk.
tttt
t
v
v
t
v
v
t
v
v
t
v
v
n
n
k
n
kkk
++++
+++
....
.....
321
3
3
2
2
1
1
.Do
v
v
k
1
;
v
v
k
1
...
v
v
k
1
<1
nên
v
v
k
1
t1+
v
v
k
1
t2.+..
v
v
k
1
tn< t1 +t2+....tn → Vk> Vtb (2) ĐPCM
Bài toán 3:
Tính v n t c trung bình c a ôtô trên c qu ng đ ng trong hai tr ng h p :ậ ố ủ ả ả ườ ườ ợ
a, N a quãng đ ng đ u ôtô đi v i v n t c vử ườ ầ ớ ậ ố 1 , N a quãng đ ng còn l i ôtô đi v i v n t c vử ườ ạ ớ ậ ố 2
b, N a th i gian đ u ôtô đi v i v n t c vử ờ ầ ớ ậ ố 1 , N a th i gian sau ôtô đi v i v n t c vử ờ ớ ậ ố 2 .
Gi i: a, G i qu ng đ ng ôtô đã đi là s . ả ọ ả ườ
Th i gian đ ôtô đi h t n a qu ng đ ng đ u là : ờ ể ế ữ ả ườ ầ
1
2
=
1
1
s
t
v
Th i gian đ ôtô đi h t n a qu ng đ ng còn l i là : ờ ể ế ữ ả ườ ạ
1
2
=
1
1
s
t
v
V n t c trung bình c a ôtô trên c qu ng đ ng: ậ ố ủ ả ả ườ
2
1 1
2 2
= = =
+ +
+
1 2
tb
1 2 1
1 2
2v v
s s
v
t t v v
s s
v v
b,G i th i gian đi h t c qu ng đ ng là tọ ờ ế ả ả ườ
N a th i gian đ u ôtô đi đ c qu ng đ ng là : ữ ờ ầ ượ ả ườ
1
2
=
1 1
s t.v
N a th i gian sau ôtô đi đ c qu ng đ ng là : ữ ờ ượ ả ườ
1
2
=
2 2
s t.v
V n t c trung bình c a ôtô trên c qu ng đ ng là : ậ ố ủ ả ả ườ
1 1
2 2
+
+ +
= = =
1 2
1 2 1 2
tb
tv tv
s s v v
v
t t 2
C/ Các bài toán v chuy n đ ng tròn đ uề ể ộ ề .
Ph ng pháp: ươ
+ ng d ng tính t ng đ i c a chuy n đ ng. Ứ ụ ươ ố ủ ể ộ
4

Tài li u b i d ng HSG – Môn V t lý 9ệ ồ ưỡ ậ
+ S l n g p nhau gi a các v t đ c tính theo s vòng chuy n đ ng c a v t đ c coiố ầ ặ ữ ậ ượ ố ể ộ ủ ậ ượ
là v t chuy n đ ng.ậ ể ộ
Bài toán 1: M t ng i đi b và m t v n đ ng viên đi xe đ p cùng kh i hành m t đ a đi m, vàộ ườ ộ ộ ậ ộ ạ ở ở ộ ị ể
đi cùng chièu trên m t đ ng tròn chu vi C = 1800m. v n t c c a ng i đi xe đ p là vộ ườ ậ ố ủ ườ ạ 1= 22,5
km/h, c a ng i đi b là vủ ườ ộ 2 = 4,5 km/h. H i khi ng i đi b đi đ c m t vòng thì g p ng i điỏ ườ ộ ượ ộ ặ ườ
xe đ p m y l n. Tính th i gian và đ a đi m g p nhau?ạ ấ ầ ờ ị ể ặ
Gi i: Th i gian đ ng i đi b đi h t m t vòng là: t = 1,8/4,5 = 0,4 hả ờ ể ườ ộ ế ộ
Coi ng i đi b là đ ng yên so v i ng i đi xe đ p. V n t c c a ng i đi xe đ p so v i ng iườ ộ ứ ớ ườ ạ ậ ố ủ ườ ạ ớ ườ
đi b là: ộ
V = v1 – v2 = 22,5 – 4,5 = 18 km/h.
Quãng đ ng c a ng i đi xe đ p so v i ng i đi b là: S = Vt = 0,4. 18 = 7,2 km. ườ ủ ườ ạ ớ ườ ộ
S vòng ng i đi xe đ p đi đ c so v i ng i đi b là: n = = 7,2/1,8 = 4 (vòng)ố ườ ạ ượ ớ ườ ộ
V y ng i đi xe đ p g p ng i đi b 4 l n. ậ ườ ạ ặ ườ ộ ầ
Khi đi h t 1 vòng so v i ng i đi b thì ng i đi xe đ p g p ng i đi b 1 l n cu i đo nế ớ ườ ộ ườ ạ ặ ườ ộ ầ ở ố ạ
đ ng. ườ
Th i gian ng i đi xe đ p đi h t m t vòng so v i ng i đi b là: t’ờ ườ ạ ế ộ ớ ườ ộ = = 1,8/18 = 0,1 h
V y:ậ
L n g p th nh t sau khi xu t phát m t th i gian là 0,1h cách v trí đ u tiên là 0,1.4,5 = 0,45 kmầ ặ ứ ấ ấ ộ ờ ị ầ
L n g p th hai sau khi xu t phát m t th i gian là 0,2h cách v trí đ u tiên là 0,2.4,5 =0, 9 kmầ ặ ứ ấ ộ ờ ị ầ
L n g p th ba sau khi xu t phát m t th i gian là 0,3h cách v trí đ u tiên là 0,3.4,5 = 1,35 kmầ ặ ứ ấ ộ ờ ị ầ
L n g p th t sau khi xu t phát m t th i gian là 0,4h cách v trí đ u tiên là 0,4.4,5 = 1,8 kmầ ặ ứ ư ấ ộ ờ ị ầ
Các kho ng cách trên đ c tính theo h ng chuy n đ ng c a hai ng i.ả ượ ướ ể ộ ủ ườ
Bài toán 2: M t ng i ra đi vào bu i sáng, khi kim gi và kim phút ch ng lên nhau và trongộ ườ ổ ờ ồ ở
kho ng gi a s 7 và 8. khi ng i y quay v nhà thì tr i đã ngã v chi u và nhìn th y kim gi ,ả ữ ố ườ ấ ề ờ ề ề ấ ờ
kim phút ng c chi u nhau. Nhìn kĩ h n ng i đó th y kim gi n m gi a s 1 và 2. Tính xemượ ề ơ ườ ấ ờ ằ ữ ố
ng i y đã v ng m t m y gi .ườ ấ ắ ặ ấ ờ
Gi i: V n t c c a kim phút là 1 vòng/ gi . V n t c c a kim gi là 1 vòng/ 12 gi . ả ậ ố ủ ờ ậ ố ủ ờ ờ
Coi kim gi là đ ng yên so v i kim phút. V n t c c a kim phút so v i kim gi là (1 – ) =ờ ứ ớ ậ ố ủ ớ ờ
vòng/gi .ờ
Th i gian đ kim gi và kim phút g p nhau gi a hai l n liên ti p là: = (gi )ờ ể ờ ặ ữ ầ ế ờ
Khi đó kim gi đi đ c 1 đo n so v i v trí g p tr c là: . = vòng.ờ ượ ạ ớ ị ặ ướ
Khi đó kim phút đã đi đ c 1 vòng tính t s 12. nên th i gian t ng ng là (1 + ) gi .ượ ừ ố ờ ươ ứ ờ
Khi g p nhau gi a s 7 và s 8 thì kim phút đã đi đ c 7 vòng, nên th i đi m đó là 7 + gi .ặ ở ữ ố ố ượ ờ ể ờ
T ng t . gi a 2 l n hai kim đ i nhau liên ti p cũng có th i gian là gi .ươ ự ữ ầ ố ế ờ ờ
Ch n t i th i đi m 6h. kim phút và kim gi đ i nhau. Thì khi t i v trí kim gi n m gi a s 1 và ọ ạ ờ ể ờ ố ớ ị ờ ằ ữ ố
s 2. thì th i gian là 7 + gi .ố ờ ờ
Ch n m c th i gian là 12h. thì khi hai kim đ i nhau mà kim gi n m gi a s 1 và s 2 thì th iọ ố ờ ố ờ ằ ữ ố ố ờ
đi m đó là (6 + 7 + ) gi .ể ờ
V y th i gian ng i đó v ng nhà là (13 + ) – (7+ ) = 6 gi . ậ ờ ườ ắ ờ
Bài toán 3: Chi u dài c a m t đ ng đua hình tròn là 300m. hai xe đ p ch y trên đ ng nàyề ủ ộ ườ ạ ạ ườ
h ng t i g p nhau v i v n t c Vướ ớ ặ ớ ậ ố 1 = 9m/s và V2 = 15m/s. Hãy xác đ nh kho ng th i gian nhị ả ờ ỏ
nh t tính t th i đi m h g p nhau t i m t n i nào đó trên đ ng đua đ n th i đi m h l i g pấ ừ ờ ể ọ ặ ạ ộ ơ ườ ế ờ ể ọ ạ ặ
nhau t i chính n i đóạ ơ
Gi i: Th i gian đ m i xe ch y đ c 1 vòng là: tả ờ ể ỗ ạ ượ 1= = (s) , t2 = = 20(s)
Gi s đi m g p nhau là M. Đ g p t i M l n ti p theo thì xe 1 đã ch y đ c x vòng và xe 2ả ử ể ặ ể ặ ạ ầ ế ạ ượ
ch y đ c y vòng. Vì chúng g p nhau t i M nên: xtạ ượ ặ ạ 1 = yt2 nên: =
X, y nguyên d ng. Nên ta ch n x, y nh nh t là x = 3, y = 5ươ ọ ỏ ấ
5




![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










