intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Tài liệu VD-VDC trích từ các đề thi thử tốt nghiệp THPT 2021 môn Toán – Chủ đề: Hình học không gian - Xác suất (Tổng hợp lần 3)

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:33

Thêm vào BST
Báo xấu
3
lượt xem 0
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu VD-VDC trích từ các đề thi thử tốt nghiệp THPT 2021 môn Toán – Chủ đề: Hình học không gian - Xác suất (Tổng hợp lần 3) được thiết kế cho học sinh lớp 12 rèn luyện kỹ năng giải bài tập tích hợp giữa hình học không gian và xác suất. Tài liệu gồm bài tập trắc nghiệm chọn lọc, công thức trọng tâm, các câu hỏi đúng sai giúp học sinh luyện kỹ năng phản xạ và phân tích. Mời các bạn cùng tham khảo tài liệu để học tập toàn diện chuyên đề tích hợp này.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tài liệu VD-VDC trích từ các đề thi thử tốt nghiệp THPT 2021 môn Toán – Chủ đề: Hình học không gian - Xác suất (Tổng hợp lần 3)

  1. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021 TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2021 CHƯƠNG 6. HHKG-XÁC SUẤT TỔNG HỢP LẦN 3 Link lần 1+2: https://drive.google.com/drive/folders/12dZ3gwX3JRHjlRtndy_uwKlj4z0_0wwp?usp=sharing PHẦN 1. GÓC VÀ KHOẢNG CÁCH Câu 1. (THPT Lê Quý Đôn - Hải Phòng - 2021) Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a ;   600 và SB  a . Hình chiếu vuông góc của điểm S lên mặt phẳng  ABC  trùng ABC với trọng tâm tam giác ABC . Gọi  là góc giữa đường thẳng SB và mặt phẳng  SCD  . Tính sin  . 3 1 1 2 A. sin   . B. sin   . C. sin   . D. sin   . 2 4 2 2 Câu 2. (THPT Lê Quý Đôn - Hải Phòng - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2 AB  2a . Cạnh bên SA  2a và vuông góc với mặt phẳng đáy. Gọi M , N lần lượt là trung điểm của SB và SD . Tính khoảng cách từ S đến mặt phẳng  AMN  . 3a a 6 A. a 5 . B. 2a . C. . D. . 2 3 Câu 3. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a . Mặt bên SAD là tam giác đều và  SAD    ABCD  . Gọi M là trung điểm của cạnh đáy AB . Khoảng cách giữa hai đường thẳng SA và CM là: a 3 a 2 a 5 a 3 A. . B. . C. . D. . 3 3 4 4 Câu 4. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình hộp ABCD. ABCD có tất cả các cạnh    đều bằng a và BAA  DAA  BAD  600. Gọi G là trọng tâm của tam giác ABC . Khoảng cách từ G đến mặt phẳng  DAC  bằng a 22 4a 11 2a 11 a 22 A. . B. . C. . D. . 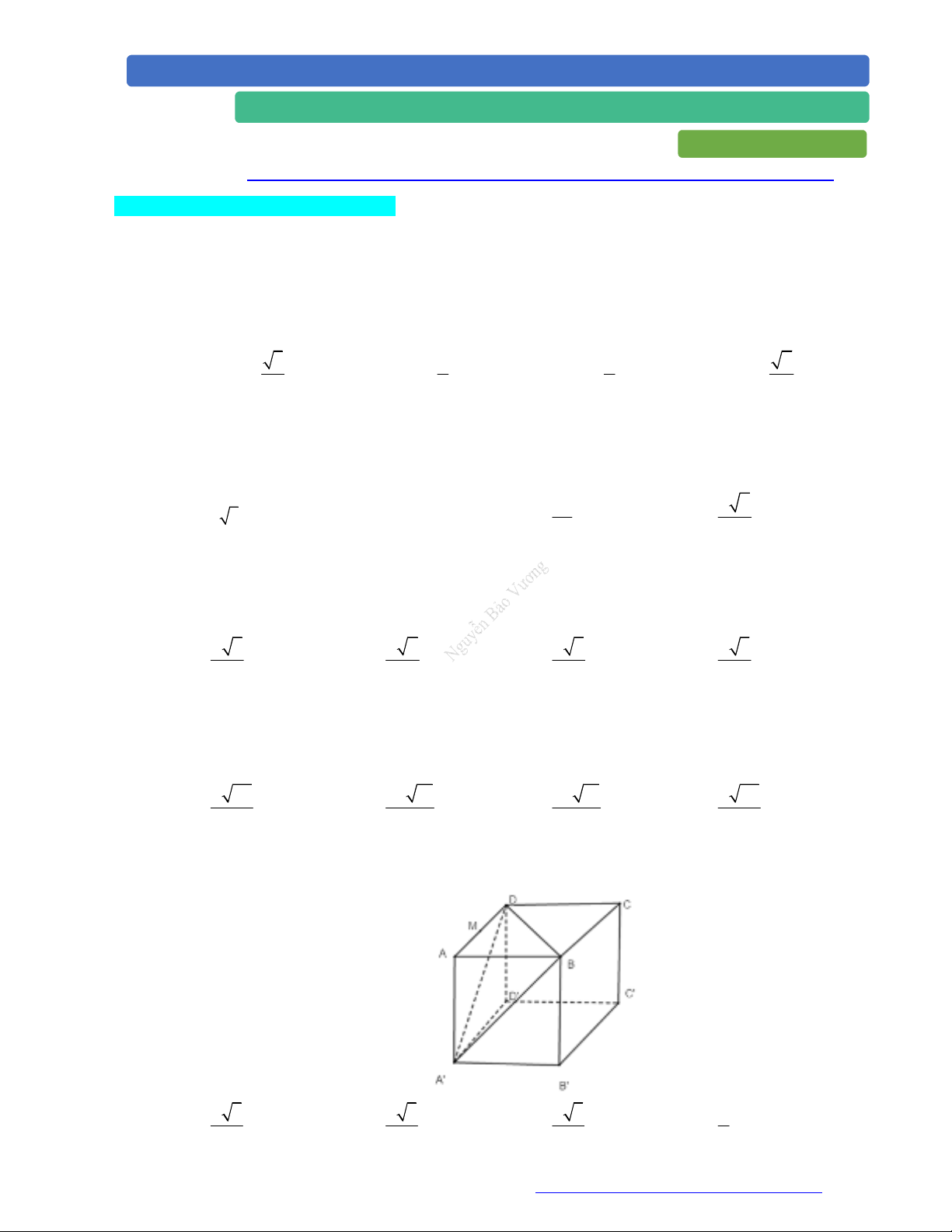66 11 11 11 Câu 5. (THPT Cẩm Bình - Hà Tĩnh - 2021) Cho hình lập phương ABCD. A ' B ' C ' D ' có cạnh bằng a . Gọi M là trung điểm của AD (tham khảo hình vẽ). Khoảng cách từ M đến mặt phẳng ( A ' BD) a 3 a 3 a 3 a A. . B. . C. . D. . 6 12 3 2 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
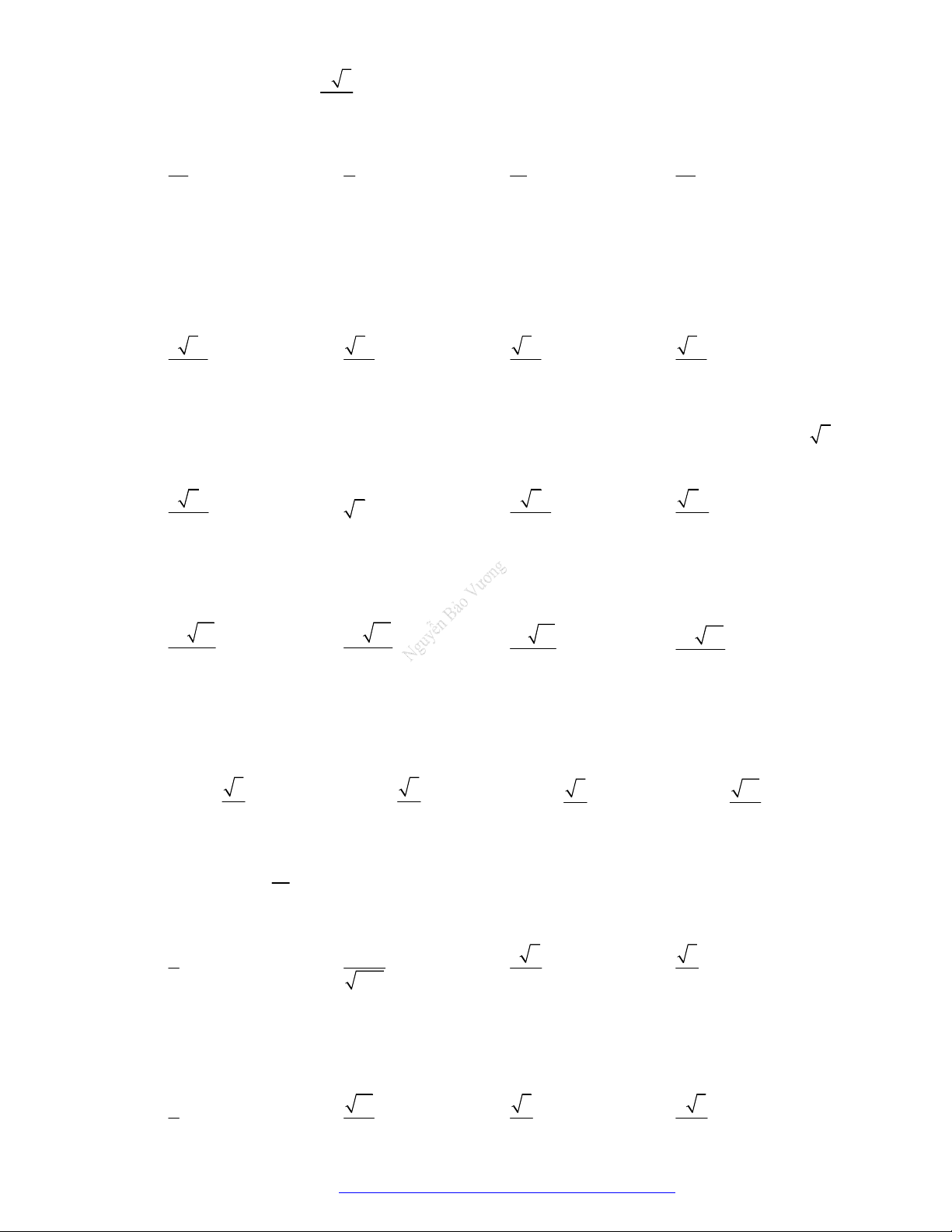
  2. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Câu 6. (THPT Trần - Hà Tĩnh - 2021) Cho hình chóp đều S . ABC . Biết Phú a 3 SA  SB  SC  a , AB   là góc giữa hai mặt phẳng  SAC  và  SBC  . Giá trị của 2 . Gọi cos  bằng 11 2 5 11 A. . B. . C. . D. . 42 5 13 43 Câu 7. (Sở Ninh Bình - 2021) Cho lăng trụ ABC. ABC  có đáy là tam giác ABC vuông tại A với AC  a . Biết hình chiếu vuông góc của B  lên mặt phẳng  ABC  là trung điểm H của BC . Mặt phẳng  ABBA tạo với mặt phẳng  ABC  một góc 60 o . Gọi G là trọng tâm tam giác BCC  . Tính khoảng cách từ G đến mặt phẳng  ABBA  . 3 3a 3a 3a 3a A. . B. . C. . D. . 4 4 2 3 Câu 8. (THPT Thanh Chương 1 - Nghệ An - 2021) Cho hình chóp S. ABC có đáy là tam giác đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết SA  a 6. Khoảng cách từ điểm A đến mặt phẳng (SBC ) bằng 3 7a 6 7a 7a A. . B. 7a . C. . D. . 7 7 2 Câu 9. (Nam Định - 2021) Cho hình hộp chữ nhật ABCD. AB ' C ' D có AB  BC  a và CC   2a . Gọi M và N lần lượt là trung điểm của cạnh BC và AA . Khoảng cách giữa hai đường thẳng B D  và MN bằng 5a 17 5a 17 3a 17 3a 17 A. . B. . C. . D. . 17 68 68 76 Câu 10. (THPT Quãng Xương 1-Thanh Hóa - 2021) Cho hình lăng trụ ABC. ABC có AB  CB  2 , AC  1 . Mặt phẳng  P  cắt các đường thẳng AA , BB , CC  lần lượt tại M , N , P sao cho tam giác MNP đều. Gọi  là góc tạo bởi  P  và mặt phẳng  ABC  , khi đó: 3 5 5 10 A. cos   . B. cos   . C. cos   . D. cos   . 3 3 5 5 Câu 11. (Sở Đồng Tháp 2021) Cho hình hộp đứng ABCD. A ' B ' C ' D ' , đáy ABCD là một hình bình hành 18  có diện tích bằng , AB  2, AD  3, BAD là góc nhọn, AA '  1 . Khoảng cách giữa hai mặt phẳng 5  A ' BD  ,  CB ' D  bằng 6 18 3 2 3 A. B. C. D. 7 409 7 2  Câu 12. (Sở Đồng Tháp 2021) Cho hình chóp S . ABCD có đáy ABCD là hình thoi, BAD  60 , tam giác SBD là tam giác đều, SA  2 SC . Tính cô-sin của góc hợp bởi đường thẳng SB và mặt phẳng  ABCD  . 1 13 3 2 3 A. . B. . C. . D. . 2 5 3 5 Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  3. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021 Câu 13. (Chuyên Lê Thánh Tông - Quảng Nam - 2021) Cho hình nón đỉnh S , đáy là đường tròn tâm O bán kính R  5 , góc ở đỉnh bằng 60 . Một mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho AB  8 . Tính khoảng cách từ O đến  SAB  . 3 13 15 7 15 13 15 34 A. . B. . C. . D. . 4 14 26 34 Câu 14. (Chuyên Lê Thánh Tông - Quảng Nam - 2021) Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc và AB  a , AC  a 2 , AD  a 3 . Tính khoảng cách d từ điểm A đến mặt phẳng  BCD  . a 6 a 3 a 30 a 66 A. d  . B. d  . C. d  . D. d  . 3 2 5 11 Câu 15. (Chuyên Lê Thánh Tông - Quảng Nam - 2021) Một chiếc hộp hình hộp chữ nhật ABCD.EFGH , mặt trên EFGH không nắp (xem hình bên). Có một con kiến ở đỉnh A bên ngoài hộp và một miếng mồi của kiến tại điểm O là tâm đáy ABCD ở bên trong hộp. Tính quãng đường ngắn nhất mà con kiến tìm đến miếng mồi (làm tròn đến một chữ số thập phân). A. 12,3 . B. 12, 4 . C. 12, 2 . D. 12,8 . Câu 16. (THPT Trần Nhân Tông - Quảng Ninh - 2021) Cho hình lăng trụ ABC. A ' B ' C ' có chiều cao 3 9 a . Biết rằng tam giác A ' BC là tam giác nhọn và nằm trong mặt phẳng vuông góc với mặt 35 đáy. Hai mặt phẳng  ABB ' A ' và  ACC ' A ' cùng tạo với đáy các góc bằng nhau. Góc  BAC  600 , AC  3 AB  3a . Khoảng cách giữa hai đường thẳng AB ' và A ' C bằng 2a a 3a A. . B. . C. a . D. . 3 3 2 Câu 17. (THPT Thanh Oai - Hà Nội - 2021) Cho hình chóp S . ABCD có đáy ABCD là hình thang vuông tại A và B . Biết AB  BC  1 , AD  2 . Các mặt chéo  SAC  và  SBD  cùng vuông góc với mặt đáy  ABCD  . Biết góc giữa hai mặt phẳng  SAB  và  ABCD  bằng 60 . Khoảng cách từ điểm D đến mặt phẳng  SAB  là 2 3 3 A. 2 3 . B. . C. 3. D. . 3 3 PHẦN 2. XÁC SUẤT Câu 18. (THPT Thanh Chương 1 - Nghệ An - 2021) Xếp 9 học sinh gồm 2 học sinh lớp 12A, 2 học sinh lớp 12B và 5 học sinh lớp 12C (trong 5 học sinh lớp 12C có hai bạn An và Bình) thành một hàng Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
  4. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 ngang. Xác suất để mỗi học sinh lớp 12B đều được đứng ở giữa hai học sinh lớp 12C, đồng thời hai bạn An và Bình luôn đứng cạnh nhau bằng 1 1 1 1 A. . B. . C. . D. . 105 132 1260 210 Câu 19. (Bắc Ninh - 2021) Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số được lập từ tập X  0;1;2;3;4;5;6;7 . Rút ngẫu nhiên một số từ S . Tính xác suất để rút được số mà trong số đó, chữ số đứng sau luôn lớn hơn hoặc bằng chữ số đứng trước. 3 2 3 11 A. . B. . C. . D. . 32 7 16 64 u1  2 Câu 20. (Bắc Ninh - 2021) Cho dãy số  un  được xác định như sau:  . Tính un 1  4un  4  5n ( n  1) tổng S  u2021  2u2020 . A. S  2019  3.42021 . B. S  2018  3.42020 . C. S  2018  3.42020 . D. S  2019  3.42021 . 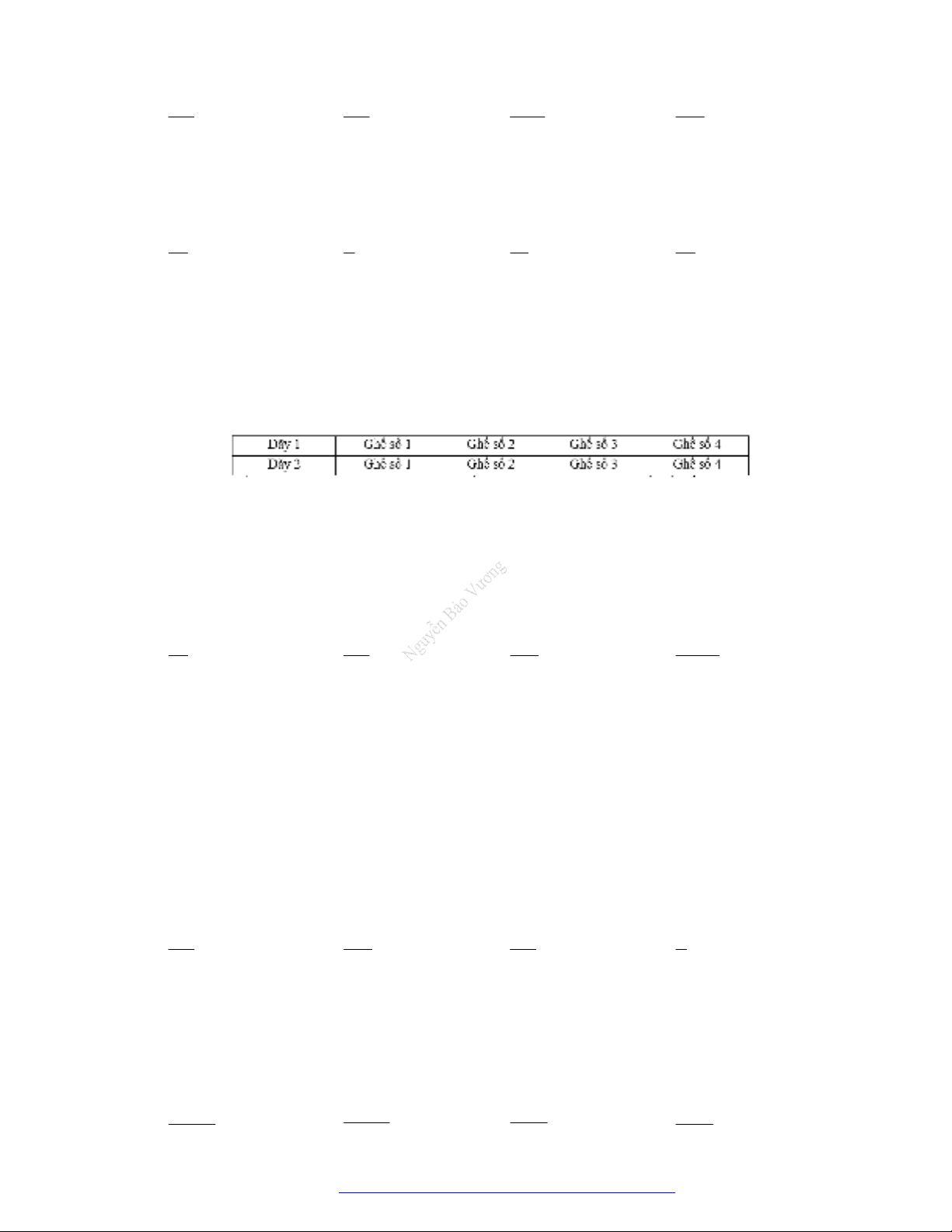Câu 21. (Bắc Ninh - 2021) Cho 2 dãy ghế được xếp như sau: Xếp 4 bạn nam và 4 bạn nữ vào hai dãy ghế trên. Hai người được gọi là ngồi đối đối diện với nhau nếu ngồi ở hai dãy và có cùng vị trí ghế (số ở ghế). Số cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ bằng A. 4!.2 . B. 4!4! . C. 4!4!.2 . D. 4!4!.2 4 . Câu 22. (Nam Định - 2021) Xếp ngẫu nhiên 7 học sinh nữ và 5 học sinh nam vào 12 ghế thành một hàng ngang. Tính xác suất để không có bất kỳ hai học sinh nam nào ngồi cạnh nhau 7 1 7 7 A. . B. . C. . D. . 99 132 264 11880 Câu 23. (Chuyên Lê Hồng Phong - 2021) Một mật mã HP là một dãy 10 kí tự gồm 3 chữ cái in hoa kề nhau (trong bảng chữ cái tiếng Anh) và sau đó là 7 chữ số kế nhau (ví dụ: AAA0000000). Chọn ngẫu nhiên 1 mật mã HP. Gọi S là xác xuất để mã được chọn không chứa chữ cái A hoặc không có chữ số 0. Khẳng định nào sau đây đúng? A. S   90%;93%  . B. S   94%; 95%  . C. S   93%;94%  . D. S   95%;99%  . Câu 24. (Chuyên Biên Hòa - 2021) Gọi S là tập hợp các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số trong tập S . Tính xác suất để số được chọn có đúng bốn chữ số lẻ và chữ số 0 có hai chữ số kề nó là chữ số lẻ 2 21 20 1 A. . B. . C. . D. . 189 200 189 2 Câu 25. (THPT Lê Quý Đôn - Hải Phòng - 2021) Có 18 bạn thi Toán và KHTN bằng Tiếng Anh được khen thưởng gồm 9 nam và 9 nữ, tất cả các học sinh nam có chiều cao khác nhau, học sinh nữ có chiều cao khác nhau. Thầy Chinh xếp ngẫu nhiên các bạn thành một hàng ngang để chụp ảnh kỉ niệm sao cho tính từ trái sang phải các học sinh nam có chiều cao giảm dần và các học sinh nữ có chiều cao tăng dần. Xác suất để các bạn nam và các bạn nữ đứng xen kẽ theo cách trên là 1 1 1 14 A. . B. . C. . D. . 24310 48620 2002 2002 Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  5. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021 Câu 26. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Có 30 quả cầu được đánh số tự nhiên từ 1 đến 30. Lấy ngẫu nhiên đồng thời hai quả cầu rồi nhân các số trên hai quả cầu lại với nhau. Tính xác suất để số nhận được là số chia hết cho 10. 48 8 16 16 A. . B. . C. . D. . 145 29 29 145 Câu 27. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Gọi S là tập hợp tất cả các số tự nhiên gồm 6 chữ số và các chữ số thuộc tập hợp 1; 2;3; 4 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó có mặt chữ số 1 ít nhất một lần bằng 729 5 91 3367 A. . B. . C. . D. . 2048 6 1024 4096 Câu 28. (THPT Nuyễn Công Trứ - Hà Tĩnh - 2021) Chọn ngẫu nhiên 3 số a, b, c trong tập hợp m S  1;2;...;26 . Biết xác suất để 3 số chọn ra thỏa mãn a 2  b2  c2 chia hết cho 5 bằng với n m m, n  * và là phân số tối giản. Tính giá trị biểu thức T  m  n . n A. 104 . B. 100 . C. 81 . D. 79 . Câu 29. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Gọi S là tập hợp các số tự nhiên có 6 chữ số. Chọn ngẫu nhiên một số từ S , tính xác suất để các chữ số của số đó đôi một khác nhau và phải có mặt chữ số 0 và 1 . 7 7 7 189 A. . B. . C. . D. . 150 375 125 1250 Câu 30. (Chuyên Bắc Ninh - 2021) Cho tập A  1, 2,3, 4,5, 6, 7,8 . Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao cho các số này lẻ và không chia hết cho 5 ? A. 20100 . B. 12260 . C. 40320 . D. 15120 . Câu 31. (Chuyên Bắc Ninh - 2021) Cho n là số tự nhiên có bốn chữ số bất kì. Gọi S là tập hợp tất cả các số thực  thoả mãn 3  n . Chọn ngẫu nhiên một phần tử của S . Xác suất để chọn được một số tự nhiên bằng 1 1 1 A. . B. . C. . D. 0. 4500 3000 2500 Câu 32. (Sở Phú Thọ - 2021) Một đội thanh niên tình nguyện của trường gồm có 6 học sinh nam và 5 học sinh nữ. Chọn ngẫu nhiên 4 học sinh để cùng với các giáo viên tham gia đo thân nhiệt cho hoc sinh khi đến trường. Xác suất để chọn được 4 học sinh trong đó số học sinh nam bằng số hoc sinh nữ bằng 5 5 6 2 A. . B. . C. . D. . 66 11 11 33 Câu 33. (THPT Cẩm Bình - Hà Tĩnh - 2021) Cho tập hợp X  1; 2;3; 4;5;6;7;8;9 . Gọi A là tập hợp các số tự nhiên có bốn chữ số được lập từ các chữ số thuộc tập X . Chọn ngẫu nhiên một số từ A , xác suất để số được chọn chia hết cho 6 bằng 4 1 4 9 A. . B. . C. . D. . 9 9 27 28 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
  6. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Câu 34. (THPT Quãng Xương 1-Thanh Hóa - 2021) Biết rằng x, y là các số thực dương sao cho 3 số u1  8 x  log 2 y , u2  2 x log 2 y , u3 =5y theo thứ tự đó lập thành một cấp số cộng và một cấp số nhân. Khi đó 2 x. y 2 có giá trị bằng: A. 10 . B. 5 . C. 5. D. 1. Câu 35. (THPT Quãng Xương 1-Thanh Hóa - 2021) Trong buổi sinh hoạt nhóm của lớp, tổ một có 12 học sinh gồm 4 học sinh nữ trong đó có Dung và 8 học sinh nam trong đó có Hải. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất 1 học sinh nữ. Tính xác suất để Dung và Hải thuộc cùng một nhóm. 5 11 3 7 A. . B. . C. . D. . 16 16 16 16 Câu 36. (Sở Đồng Tháp 2021) Cho đa giác đều có 12 đỉnh được đặt tên bằng 12 chữ cái khác nhau, chọn ngẫu nhiên 4 chữ cái trong 12 chữ cái đó. Xác suất của biến cố: “bốn chữ cái được chọn là 4 đỉnh của một hình chữ nhật”. 1 2 1 1 A. . B. . C. . D. . 33 33 15 3 Câu 37. (THPT Trần Nhân Tông - Quảng Ninh - 2021) Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi học sinh giỏi có 10 bạn trong đội tuyển gồm 2 bạn đến từ lớp 12A1, 3 bạn từ 12A2, 5 bạn còn lại đến từ các lớp khác nhau. Thầy giáo xếp ngẫu nhiên các bạn kể trên ngồi vào một bàn dài mỗi bên 5 ghế xếp đối diện nhau. Tính xác suất sao cho không có học sinh nào cùng lớp ngồi đối diện nhau. 73 53 5 38 A. . B. . C. . D. . 126 126 9 63 Câu 38. (THPT Thanh Oai - Hà Nội - 2021) Ba bạn tên là Xuân, Tân, Sửu mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn 1;19 . Xác suất để ba số viết ra có tổng chia hết cho 3 là 3272 2287 1512 775 A. 6859 B. 6859 C. 6859 D. 6859 Theo dõi Fanpage: Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Hoặc Facebook: Nguyễn Vương  https://www.facebook.com/phong.baovuong Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN)  https://www.facebook.com/groups/703546230477890/ Ấn sub kênh Youtube: Nguyễn Vương  https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber Tải nhiều tài liệu hơn tại: http://diendangiaovientoan.vn/ ĐỂ NHẬN TÀI LIỆU SỚM NHẤT NHÉ! Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  7. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021 TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2021 CHƯƠNG 6. HHKG-XÁC SUẤT TỔNG HỢP LẦN 3 Link lần 1+2: https://drive.google.com/drive/folders/12dZ3gwX3JRHjlRtndy_uwKlj4z0_0wwp?usp=sharing PHẦN 1. GÓC VÀ KHOẢNG CÁCH Câu 1. (THPT Lê Quý Đôn - Hải Phòng - 2021) Cho hình chóp  S. ABCD  có đáy  ABCD  là hình thoi  cạnh  a ;    600  và  SB  a . Hình chiếu vuông góc của điểm  S  lên mặt phẳng   ABC   trùng  ABC với trọng tâm tam giác  ABC . Gọi    là góc giữa đường thẳng  SB  và mặt phẳng   SCD  . Tính  sin  .  3 1 1 2 A. sin   . B. sin   . C. sin   . D. sin   .  2 4 2 2 Lời giải Chọn D    AB  AC  a  Vì    ABC  là tam giác đều cạnh  a .    ABC  60   Gọi  G  là trọng tâm của tam giác  ABC    SG   ABCD  .  Gọi  E  là hình chiếu của  B  trên   SCD   nên  SE  là hình chiếu của  SB  trên mặt phẳng   SCD        Góc  giữa  SB   và  mặt  phẳng   SCD    là  góc  giữa  hai  đường  thẳng  SB , SE   và  bằng  BSE     BSE   .  Ta có  BE  d  B,  SCD   .  d  B,  SCD   BG 3 3 BG   SCD   D     d  B, CD   d  G ,  SCD     d  G ,  SCD   GC 2 2 Kẻ  GH  SC  tại  H 1 .  CD  CG Ta có:    CD   SCG   CD  HG  2  .   CD  SG Từ  1  và   2  suy ra  GH   SCD   d  G,  SCD    GH .  2 a 3 a CG  .  .  3 2 3 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
  8. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489  a2 a 6 Xét tam giác  SBG  vuông tại  G  có  SG  SB 2  AG 2  a 2   .  3 3 Xét  tam  giác  SCG   vuông  tại  G  ta  có  1 1 1 9 3 9 a 2 3 a 2 2  2  2  2  2  2  HG   BE  HG  .Xét  tam  giác  SEB   HG GS GC 6a a 2a 3 2 2 a 2 BE 2  2 .  vuông tại  E  ta có  sin    SB a 2 Câu 2. (THPT Lê Quý Đôn - Hải Phòng - 2021) Cho hình chóp  S. ABCD  có đáy  ABCD  là hình chữ  nhật với  AD  2 AB  2a . Cạnh bên  SA  2a  và vuông góc với mặt phẳng đáy. Gọi  M ,  N  lần  lượt là trung điểm của  SB  và  SD . Tính khoảng cách từ  S  đến mặt phẳng   AMN  . 3a a 6 A. a 5 . B. 2a . C. . D. .  2 3 Lời giải Chọn D   1 1 1 2 3 Ta có:  VS . ABD  VS . ABCD  AS . AB. AD  2a.a.2a  a .  2 6 6 3 VS . AMN SA SM SN 1 1 1 1 1 2 1  . .  1. .   VS . AMN  VS . ABD  . a 3  a 3 .  VS . ABD SA SB SD 2 2 4 4 4 3 6 1 1 1 2 a 5 Mặt khác:  AM SB  AB 2  AS 2  a  4a 2  .  2 2 2 2 1 1 1 AN  SD  AD 2  AS 2  4a 2  4a 2  a 2 .  2 2 2 1 1 1 2 a 5 MN  BD  AB 2  AD 2  a  4a 2  .  2 2 2 2 a2 6 Suy ra:  S AMN  .  4 3VS . AMN 1 3 4 a 6 Vậy  d  S ;  AMN     a. 2  .  S AMN 2 a 6 3 Câu 3. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho  hình  chóp  S. ABCD   có  đáy  ABCD   là  hình  vuông cạnh  a . Mặt bên  SAD  là tam giác đều và   SAD    ABCD  . Gọi  M  là trung điểm của  cạnh đáy  AB . Khoảng cách giữa hai đường thẳng  SA  và  CM  là:  Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  9. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021  a 3 a 2 a 5 a 3 A. .  B. .  C. .  D. .  3 3 4 4 Lời giải Chọn D   Gọi  H ;  N ;  E  lần lượt là trung điểm  AD ;  CD ;  AN   Từ gt  SH  AD  nên  SH   ABCD    Dễ thấy  CM / /  SAN     d  SA ; CM   d  CM ;  SAN    d  C ;  SAN    d  D ;  SAN    2d  H ;  SAN     1 a 1 1 a a 3 Mà  HA  AD  ;  HE  DN  CD  ;  HS  SA.sin 60    2 2 2 4 4 2 HA ;  HE ;  HS  đôi một vuông góc  1 1 1 1 a 3  2  2  2  2  d  H ;  SAN       d  H ;  SAN    HA HE HS 8   a 3  d  SA ; CM   2d  H ;  SAN    .  4 Câu 4. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình hộp  ABCD. ABCD  có tất cả các cạnh     đều bằng  a  và  BAA  DAA  BAD  600.  Gọi  G  là trọng tâm của tam giác  ABC . Khoảng cách  từ  G  đến mặt phẳng   DAC   bằng  a 22 4a 11 2a 11 a 22 A. .  B. .  C. .  D. .  66 11 11 11 Lời giải Chọn D Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
  10. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489  Gọi  H  là trọng tâm tam giác  ABD  và  K  là trung điểm  AD.      Do  BAA '  DAA '  BAD  600  và  AA  AB  AD  AB  AD  BD  a.   a3 2  A ' ABD  là tứ diện đều cạnh bằng  a  VAABD  .  12 a 6 a3 2   đường cao  A ' H  ,  VD.DAC   VD. AC D  VAABD  .  3 12 Xét  DA ' C ', có  A ' D  a, A ' C '  DC '  a 3.   2 2 a a 11 1 a 2 11  C K   a 3     2 2  S DA 'C '  AD.C K  2 4 .  Do  G  là trọng tâm của tam giác  A ' BC '  và  BO //OD   a3 2 3VD.DAC  3. a 22  d  G ,  DAC     d  B,  DAC     d  D,  DAC      2 12  .  S DAC  a 11 11 4 a 22 Vậy khoảng cách từ  G  đến mặt phẳng   DAC   bằng  .  11 Câu 5. (THPT Cẩm Bình - Hà Tĩnh - 2021) Cho hình lập phương  ABCD. A ' B ' C ' D ' có cạnh bằng  a .  Gọi  M  là trung điểm của  AD  (tham khảo hình vẽ). Khoảng cách từ  M đến mặt phẳng  ( A ' BD)     a 3 a 3 a 3 a A. .  B. .  C. .  D. .  6 12 3 2 Lời giải Chọn A Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  11. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021    Gọi  O  là giao điểm của  AC  và  BD . Ta có:  AA '  ( ABCD)  BD  AA '  BD   Lại có:  AO  BD ( tính chất 2 đường chéo hình vuông)   ( A ' AO)  BD  ( A ' BD)    ( A ' AO)  ( A ' BD) Mà  ( A ' AO)  ( A ' BD)  A ' O   kẻ  AH  A ' O, H  A ' O  suy ra  d ( A, ( A ' BD))  AH   1 1 1 1 1 3 mà  2  2  2  2 2  2  AH AA ' AO a a 2 a    2  a suy ra  AH  = d ( A,( A ' BD))   3 Lại có:  A, M  ( A ' BD ); AM  ( A ' BD )  {D}   d ( A, ( A ' BD )) AD d ( A, ( A ' BD )) a 3 nên    2  d ( M ; ( A ' BD ))   . Chọn  A. d ( M ; ( A ' BD )) MD 2 6 Câu 6. (THPT Trần Phú - Hà Tĩnh - 2021) Cho  hình  chóp  đều  S . ABC .  Biết  a 3 SA  SB  SC  a , AB  .  Gọi     là  góc  giữa  hai  mặt phẳng   S AC    và   SBC  .  Giá  trị  của  2 cos   bằng  11 2 5 11 A. .  B. .  .  C. D. .  42 5 13 43 Lời giải Chọn C S H I A C O J B  Gọi  O  là tâm của  ABC .   Vì  SA  SB  SC nên  SO   ABC     Gọi  I , J  lần lượt là trung điểm của  AC , BC  I J  là đường trung bình của  ABC   Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
  12. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489   I J // AB .   Mà  CO  AB  nên  I J  CO    Ta lại có : SO   ABC   SO  IJ .   IJ  CO  Như vậy :    IJ   SOC   IJ  SC (1).   IJ  SO  Trong  SAC  kẻ  IH  SC (2).   Từ (1) và (2) ta có :   IJH   SC  JH  SC .   SAC    SBC   BC       SC  IH   SAC     SAC  ,  SBC     IH , JH  .    SC  JH   SBC  3a 2 a 3 2 2 a2  . SI IH SI .IC SC  IC .IC 16 4  a 39  HJ .      IH    SC IC SC SC a 16 39a 2 39a 2 3a 2 2 2 2   IH  HJ  IJ 256 16  5 .    cos    256 2 IH .HJ a 39 a 39 13 2. . 16 16 Câu 7. (Sở Ninh Bình - 2021) Cho  lăng  trụ  ABC. ABC    có  đáy  là  tam  giác  ABC   vuông  tại  A   với  AC  a .  Biết  hình chiếu  vuông góc của  B    lên  mặt  phẳng   ABC    là trung  điểm  H   của  BC .  Mặt  phẳng   ABBA    tạo  với  mặt  phẳng   ABC    một  góc  60 o .  Gọi  G   là  trọng  tâm  tam  giác  BCC  . Tính khoảng cách từ  G  đến mặt phẳng   ABBA  .  3 3a 3a 3a 3a A. .  B. .  C. .  D. .  4 4 2 3 Lời giải Chọn D   Gọi  I  là trung điểm cạnh  AB .  AC a Suy ra  IH    và  IH / / AC  IH  AB 1 .  2 2 Mặt khác  BH  AB  2  .  Từ (1) và (2) suy ra  AB   BIH   AB  IH  và  AB  B I .  Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  13. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021    Vậy góc giữa mặt phẳng   ABBA   với mặt phẳng   ABC   là góc  BIH  hay  BIH  60o .  Trong   BIH   kẻ  HK  B I  với  K  B I .  Mà  HK  AB  nên ta có  HK   ABBA  . Vậy  d  H ,  ABBA    HK .  GB 2 2 2 Ta có    d  G,  ABBA    d  C ,  ABBA    d  C ,  ABBA   .  C B 3 3 3 CB Do   2  d  C ,  ABBA    2d  H ,  ABBA   .  HB 4 4 Suy ra  d  G,  ABBA    d  H ,  ABBA    HK .  3 3  a 3 Trong   B IH  vuông tại  H  ta có  B H  IH . tan B IH  IH . tan 60o  .  2 1 1 1 1 4 4 1 16 a 3 Suy ra  2  2  2  2  2 2  2  2  HK  .  HK HI B H HK a 3a HK 3a 4 4 a 3 Vậy  d  G ,  ABBA    HK  .  3 3 Câu 8. (THPT Thanh Chương 1 - Nghệ An - 2021) Cho hình chóp S. ABC có đáy là tam giác đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết SA  a 6. Khoảng cách từ điểm A đến mặt phẳng (SBC ) bằng  3 7a 6 7a 7a A. .  B. 7a .  C. .  D. .  7 7 2 Lời giải Chọn C S K A C H M N B    Kẻ  SH  AB ( H là trung điềm AB ). Suy ra SH  ( ABC ) .   Có  AB 2  SA2  SB 2  2 SA2  AB  SA 2  a 12  2a 3.    Và  d ( A, ( SBC ))  2d ( H , ( SBC ))    Từ  H  kẻ  HN  BC  ( HN / / AM  với  M  là trung điểm  BC ) và kẻ  HK  SN .   Ta có  HN  BC  và  SH  BC  nên BC   SHN  , suy ra HK  BC .   Mặt khác  HK  BC  và  HK  SN  nên HK   SBC  , suy ra d ( A,( SBC ))  2d ( H , ( SBC ))  2 HK .  1 1 1 AB 3 3a  Ta có  SH  AB  a 3 ;  HN  AM  .   và  2 2 2 2 2 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
  14. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489  1 1 1 1 4 7 3a 6a 6a 7 2  2  2  2  2  2  HK  . Do đó  d ( A, ( SBC ))   .  HK SH HN 3a 9a 9a 7 7 7 Câu 9. (Nam Định - 2021) Cho hình hộp chữ nhật  ABCD. AB ' C ' D  có  AB  BC  a  và  CC   2a . Gọi  M  và  N  lần lượt là trung điểm của cạnh  BC  và  AA . Khoảng cách giữa hai đường thẳng  B D    và  MN  bằng 5a 17 5a 17 3a 17 3a 17 A. . B. . C. . D. .  17 68 68 76 Lời giải Chọn A Cách 1. Gọi  P  là trung điểm  CD ,  I  MP  AD ,  J  IN  DD ,  K  AC  MP .  A' B' D' C' N H A B J K M D P C I   Ta có  MP //BD  MP //BD   d  BD; MN   d  BD;  MNP    d  D;  MNP   .      DJ Lại có  d  D;  MNP      d  D;  MNP    5 .  DJ   DI 1 Mặt khác  d  D;  MNP      AI d  A;  MNP    3 d  A;  MNP   .       NAK    MNP   Dễ thấy   NAK    MNP   AK  AH   MNP   d  A;  MNP    AH .      AH  NK    H  NK   trong   NAK  5 5 AA 3 3a 2 Suy ra  d  MN ; BD   d  A;  MNP    AH với  AN    3  a  ;  AK  2 AB  .  3 2 4 4 3a 2 .a 5 5 AN . AK 5 4 5a 17 Vậy  d  MN ; BD   AH  .  .  .  3 3 AN  AK2 2 3  2 17 3a 2  2   a  4  Cách 2. Đặt các trục  Ox ,  Oy  và  Oz  vào hình như sau  Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  15. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021  z A' B' D' C' N A B y M D C x   Chọn  a  2 , ta có  M 1;2;0  ,  N  0;0; 2  ,  B  0;2;4   và  D  2;0; 4  .         Ta có  MN   1; 2; 2  ,  BD   2; 2;0   và  MB   1;0; 4    MN , BD   4; 4;6  .          MN ; BD .MB  1 .4  0.4  4.6 10 17 5a 17   Khi đó  d  MN ; BD         .   MN ; BD 42  42  62 17 17   Câu 10. (THPT Quãng Xương 1-Thanh Hóa - 2021) Cho hình  lăng trụ  ABC. ABC   có  AB  CB  2 ,  AC  1 . Mặt phẳng   P   cắt các đường thẳng  AA ,  BB ,  CC   lần lượt tại  M ,  N ,  P  sao cho tam  giác  MNP  đều. Gọi    là góc tạo bởi   P   và mặt phẳng   ABC  , khi đó:  3 5 5 10 A. cos   .  B. cos   .  C. cos   .  D. cos   .  3 3 5 5 Lời giải Chọn C   Từ đề bài, ta xác định ba điểm  M ,  N ,  P  lần lượt trên ba cạnh  AA ,  BB ,  CC   sao cho tam giác  MNP  đều.  Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
  16. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489  Ta lấy điểm  N trên cạnh  BB , từ  N  kẻ đường thẳng vuông góc với mặt phẳng   AAC C   tại  I ,  suy ra  NI //  ABC  , từ  I  kẻ đường thẳng song song với  AC  cắt  AA  và  CC   lần lượt tại  F ,  E .  Từ  I  ta kẻ đường thẳng cắt  AA  và  CC   lần lượt tại  M ,  N sao cho tam giác  MNP  đều.   MNP    NEF   NI   Ta có:   NEF  / /  ABC     P  ,  ABC      MNP  ,  NEF    PIE  NI  EF , NI  MP        Đặt  PIE IE 1 1 +)  IP   ;  PE  IE.tan   tan    cos  2 cos  2 1 Suy ra:  NP 2  NE 2  EP 2  4  tan 2  .  4 2 1  1  Vì tam giác  MNP  đều nên  NP 2  MP 2  4 IP 2  4  tan 2   4.     4  2 cos   1 1  1 3 5  4  2  1  2   cos 2   cos   .  4  cos   cos  15 5 Câu 11. (Sở Đồng Tháp 2021) Cho hình hộp đứng  ABCD. A ' B ' C ' D ' , đáy  ABCD là một hình bình hành  18  có diện tích bằng  , AB  2, AD  3, BAD là góc nhọn,  AA '  1 . Khoảng cách giữa hai mặt phẳng  5  A ' BD  ,  CB ' D  bằng  6 18 3 2 3 A. B. C. D. 7 409 7 2 Lời giải Chọn B    Ta có:   A ' BD  / /  CB ' D '   d   A ' BD  ;  CB ' D '    d  C ;  CB ' D '    d  A;  CB ' D '     Kẻ  AK  BD, AH  A ' K  d  A;  CB ' D '   AH .  18 18 3 4 Ta có  S ABCD   AB. AD.sin A   sin A   cos A    5 5 5 5 Áp dụng định lý hàm cosin cho tam giác  ABD , ta có:  Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  17. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021  4 85 BD  AB 2  AD 2  2 AB. AD cos A  22  32  2.2.3.    5 5 9 2. 1 9 2.S ABD 5  18 85   Ta có  S ABD  S ABCD   AK   2 5 BD 85 85 5 18 85 .1 AK . AA ' 85 18 Suy ra:  AH    .  AK 2  AA '2 2  18 85  409 2   1  85  18 Vậy  d   A ' BD  ;  CB ' D '      409  Câu 12. (Sở Đồng Tháp 2021) Cho hình chóp  S . ABCD  có đáy  ABCD  là hình thoi,  BAD  60 , tam giác  SBD   là  tam  giác  đều,  SA  2SC .  Tính  cô-sin  của  góc  hợp  bởi  đường  thẳng  SB   và  mặt  phẳng   ABCD  . 1 13 3 2 3 A. . B. . C. . D. .  2 5 3 5 Lời giải Chọn B   a 3 Đặt  AB  a . Suy ra  BD  a ,  AC  a 3 ,  SO  .  2  BD  AC Ta có:    BD   SAC   mà  BD   ABCD      SAC    ABCD     BD  SO Suy ra hình chiếu  H  của  S  trên mặt phẳng   ABCD   thuộc giao tuyến  AC .  SA2  SC 2 AC 2 3a 2 5SC 2 3a 2 Mặt khác:  SO 2        2 4 4 2 4 3a 2 a 15 2a 15  SC 2   SC   SA  .  5 5 5 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
  18. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489  15a 2 60a 2 75a 2 Ta có:  SC 2  SA2     3a 2  AC 2 , suy ra:  SAC  vuông tại  S .  25 25 25 SA.SC a 15 2a 15 1 2a 3 SH . AC  SA.SC  SH   .  .  AC 5 5 a 3 5 Vì  SH   ABCD   nên  HB  là hình chiếu của  SB  trên mặt phẳng   ABCD   nên    SB;  ABCD    SBH .  2  SH  2a 3  2 3    cos SBH  1   2 3   1  12  13 .  sin SBH    SB 5a 5  5   25 5   Câu 13. (Chuyên Lê Thánh Tông - Quảng Nam - 2021) Cho hình nón đỉnh  S , đáy là đường tròn tâm  O   bán kính  R  5 , góc ở đỉnh bằng  60 . Một mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy  tại hai điểm  A  và  B  sao cho  AB  8 . Tính khoảng cách từ  O  đến   SAB  .  3 13 15 7 15 13 15 34 A. .  B. .  C. .  D. .  4 14 26 34 Lời giải Chọn B Gọi  I  là trung điểm  AB   OI  AB .   Mà  AB  SO  (vì  SO  vuông góc với đáy)   AB   SIO    SAB    SIO    Trong   SIO   vẽ  OK  SI   SAB    SIO   OK   SAB  .   OK  d  O,  SAB     Góc ở đỉnh bằng  60      30 , mà  OA  R  5  SA  10   ASO AB IAO  vuông tại  I  có:  OA  5, AI   4  OI  3   2 SIA  vuông tại  I  có: SI  SA2  AI 2  102  42  84   IO 2 3 21 SIO  vuông tại  O , đường cao  OK  có:  SI  84, IO  3  IK   .  SI 14 3 21 15 7 IOK  vuông tại  K  có:  IO  3, IK   OK  .  14 14 15 7 Vậy  d  O,  SAB    .  14 Câu 14. (Chuyên Lê Thánh Tông - Quảng Nam - 2021) Cho tứ diện  ABCD có  AB ,  AC ,  AD đôi một      vuông góc và  AB  a ,  AC  a 2 ,  AD  a 3 . Tính khoảng cách  d  từ điểm  A  đến mặt phẳng   BCD  .  Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  19. TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2021  a 6 a 3 a 30 a 66 A. d  . B. d  . C. d  . D. d  .  3 2 5 11 Lời giải Chọn D  AB  AC   Ta có     AB   ACD   AB  AC     1 1 1 a3 6  VABCD  AB.S ACD  .a. a 2.a 3  . 3 3 2 6    Xét tam giác  ABC  vuông tại  A  có  BC  AB 2  AC 2  a 3 .   Xét tam giác  ACD  vuông tại  A  có  CD  AD 2  AC 2  a 5 .   Xét tam giác  ABD  vuông tại  A  có  BD  AD 2  AB 2  2a .   2 2 2  BC  BD  CD  1  Xét tam giác  CBD  có  cos CBD  2.BC.BD 2 3  2   1  11  sin CBD  1     . 2 3 2 3   1  1 11 a 2 11 Khi đó  SCBD  .CB.CD.sin CBD  .a 3.2a.  .  2 2 2 3 2 a3 6 3. 3VABCD a 66  Vậy  d   2 6  .  SCBD a 11 11 2 Câu 15. (Chuyên Lê Thánh Tông - Quảng Nam - 2021) Một  chiếc  hộp  hình  hộp  chữ  nhật  ABCD.EFGH , mặt trên  EFGH  không nắp (xem hình bên).  Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
  20. TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489    Có một con kiến ở đỉnh  A  bên ngoài hộp và một miếng mồi của kiến tại điểm  O  là tâm đáy  ABCD  ở bên trong hộp. Tính quãng đường ngắn nhất mà con kiến tìm đến miếng mồi (làm tròn  đến một chữ số thập phân).  A. 12,3 .  B. 12, 4 .  C. 12, 2 .  D. 12,8 .  Lời giải Chọn C Để quãng đường ngắn nhất mà con kiến tìm đến miếng mồi thì kiến phải đi từ  A  qua mặt phẳng  AEHD  (mặt ngoài hộp) rồi tiếp tục qua mặt phẳng  AEHD  (mặt trong hộp) sau đó đến  O .  Trải phẳng quãng đường đi của kiến ta được:    Vậy đoạn  AO  là quãng đường đi ngắn nhất của kiến và  AO  22 12 2  12, 2 . Câu 16. (THPT Trần Nhân Tông - Quảng Ninh - 2021) Cho hình lăng trụ  ABC. A ' B ' C '  có chiều cao  3 9 a . Biết rằng tam giác  A ' BC  là tam giác nhọn và nằm trong mặt phẳng vuông góc với mặt  35 đáy.  Hai  mặt  phẳng   ABB ' A '   và   ACC ' A '   cùng  tạo  với  đáy  các  góc  bằng  nhau.  Góc   BAC  600 , AC  3 AB  3a . Khoảng cách giữa hai đường thẳng  AB '  và  A ' C  bằng  2a a 3a A. .  B. .  C. a .  D. .  3 3 2 Lời giải Chọn A Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright ©2025 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
3=>0