Tuyển tập Hội nghị Khoa học thường niên năm 2018. ISBN: 978-604-82-2548-3
354
TIẾP CẬN TỔNG QUÁT XÁC ĐỊNH
CÁC ĐẶC TRƯNG MẶT CẮT NGANG PHỨC TẠP
Nghiêm Tiến Dũng, Nghiêm Tiến Lam
Trường Đại học Thủy lợi, email: lam.n.t@tlu.edu.vn
1. GIỚI THIỆU CHUNG
Công tác thiết kế và vận hành các công
trình thủy lợi ngày nay đang ứng dụng rộng
rãi các phần mềm máy tính. Để giải các bài
toán thủy lực như tính toán độ sâu giới hạn
và độ sâu dòng đều, các phần mềm cần phải
tính toán các đặc trưng hình học và thủy lực
của mặt cắt như bán kính thủy lực, diện tích
mặt cắt ướt, độ rộng mặt nước, chu vi ướt và
các đạo hàm của chúng cho các mặt cắt
ngang của các loại kênh hở hoặc đường ống
dẫn nước kín.
Với một số mặt cắt đơn giản như mặt cắt
hình chữ nhật, hình thang hoặc các đường
ống hình tròn, các đăc trưng mặt cắt và đạo
hàm của chúng có thể xác định một cách dễ
dàng bằng các công thức giải tích.
Với các mặt cắt phức tạp, việc xác định
các công thức giải tích thường khó khăn hơn
và vẫn chưa có nhiều công trình nghiên cứu
được công bố. Ngoại trừ các công thức giải
tích cho các đặc trưng của mặt cắt ngang
dạng móng ngựa tiêu chuẩn của Merkley
(2005) và Samani et al. (2013), và mặt cắt
hình chữ D của Samani et al. (2013), nhiều
tác giả mới chỉ đưa ra các biểu thức xác định
các đặc trưng mặt cắt dạng ẩn thông qua các
góc ở tâm mà không biểu diễn được trực tiếp
qua độ sâu dòng chảy. Các công thức dạng
này có thể kể đến Wei et al. (2012); Wen và
Li (2013).
Hiện nay, nhiều phần mềm tính toán xác
định các đặc trưng của các mặt cắt phức hợp
bằng cách sử dụng các bảng tra hoặc các xấp
xỉ tuyến tính. Việc lưu trữ và nội suy các
bảng tra có nhược điểm là tốn bộ nhớ, độ
chính xác thấp, chậm, và chỉ làm sẵn cho một
số dạng mặt cắt nhất định. Độ chính xác thấp
có thể ảnh hưởng đến sự ổn định của các mô
hình số trị (Merkley, 2005). Cần thiết có một
tiếp cận giải tích tổng quát cho việc tính toán
các đặc trưng mặt cắt một cách chính xác trên
máy tính.
Nghiên cứu này sẽ đề xuất một bộ công
thức giải tích tổng quát để xác định chính xác
các đặc trưng hình học và thủy lực của một
mắt cắt phức hợp bất kỳ bao gồm nhiều đoạn
hợp thành của các đoạn thẳng, cung tròn,
cung e-líp hoặc cung parabol.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Để tính toán các đặc trưng của một mặt cắt
kín hoặc hở bất kỳ hợp thành từ các đoạn
thẳng, cung tròn, cung parabol và cung e-líp,
các công thức giải tích cơ bản cho từng loại
cung sẽ được thiết lập. Với mỗi mặt cắt nhất
định, sẽ xác định từng bộ phận của mặt cắt
ứng với một trong 4 loại cung cơ bản này và
các thông số hình học của chúng. Cuối cùng
là tính toán trên máy tính cho lần lượt các bộ
phận mặt cắt ướt ứng với độ sâu nước đã biết.
Xét một mặt cắt ngang có độ cao toàn bộ
là H, độ rộng lớn nhất là B, gọi h là độ sâu
nước, A là diện tích mặt cắt ướt, P là chu vi
ướt, T là độ rộng mặt nước, R = A/P là bán
kính thủy lực. Đạo hàm dA/dh = T luôn luôn
thỏa mãn cho mọi mặt cắt. Đạo hàm của R
được tính toán thông qua A, P và các đạo
hàm dT/dh và dP/dh của chúng. Các giá trị
độ cao đều tính so với điểm đáy thấp nhất của
mặt cắt.
Mặt cắt có thể được hợp thành từ các các
đoạn thẳng, cung tròn, cung e-líp hoặc cung
parabol cho các khoảng độ sâu nước từ hi-1
đến hi của bộ phận mặt cắt thứ i bất kỳ. Với
phần mặt cắt dưới cùng i = 1 từ h0 đến h1, giá
Tuyển tập Hội nghị Khoa học thường niên năm 2018. ISBN: 978-604-82-2548-3
355
trị diện tích bộ phận ban đầu là A0 = 0, còn
chu vi ướt bộ phận ban đầu P0 = b với đáy
phẳng, trong đó b là độ rộng của đáy phẳng,
và P0 = 0 với đáy cong.
3. KẾT QUẢ NGHIÊN CỨU
Các công thức tính toán trực tiếp các đặc
trưng mặt cắt hợp thành từ 4 loại cơ bản là
đoạn thẳng, cung tròn, e-líp và parabol khi
biết độ sâu nước như sau:
3.1. Đoạn thẳng
Kí hiệu Li(b, a; hi-1, hi) là đoạn thẳng từ hi-1
đến hi với độ rộng tại hi-1 và hi là b và a. Khi đó
hệ số độ dốc mái bên là m = ½(a - b)/(hi - hi-1).
Gọi y = (h - hi-1) là độ sâu nước tương đối.
Các kênh dẫn có mặt cắt hình thang, hình
chữ nhật (m = 0) hoặc hình tam giác (b = 0)
là đại diện cho dạng mặt cắt có mái bên là
một đoạn thẳng từ đáy kênh (h1 = 0) đến bờ
kênh (h2 = H).
Độ rộng mặt nước và đạo hàm
2T b my
,
2
dT m
dh (1)
Diện tích mặt cắt ướt
1i
A A b my y
(2)
Chu vi ướt và đạo hàm
2
12 1
i
P P y m
,
2
2 1
dP m
dh (3)
3.2. Cung parabol
Kí hiệu Pi(p, xc, yc; hi-1, hi) là cung parabol
từ hi-1 đến hi với đỉnh tại (xc,yc) và khoảng
cách từ đỉnh đến tiêu cự là p. Nếu toàn bộ
mặt cắt ngang kênh là một cung parabol thì p
= 4H/B². Đặt y = (h - yc)/H là độ sâu tương
đối, các đặc trưng theo độ sâu nước như sau
Độ rộng mặt nước và đạo hàm
2c
T x B y
, 2
dh
(4)
Chu vi ướt và đạo hàm
1 1
i i
P P h h
,
4 1
24
HpydP
dh
Hpy
,
4 1 4
1
2ln 4 1 4
Hpy Hpy
hp
Hpy Hpy
(5)
Diện tích mặt cắt ướt
1 1
3
,
2
23
i i
c
A A h h
h x Hy BH y
(6)
3.3. Cung tròn
Kí hiệu Ci(r, xc, yc; hi-1, hi) là cung tròn từ
hi-1 đến hi với tâm tại (xc,yc) và bán kính là r.
Đặt y = (h - yc)/r là độ sâu tương đối.
Độ rộng mặt nước và đạo hàm
2
2 2 1
c
T x r y
,
2
1
dT y
dh
y
(7)
Diện tích mặt cắt ướt
1 1
2 2
,
2 asin 1
i i
c
A A h h
h x h r y y y
(8)
Chu vi ướt và đạo hàm
1 1
,
2 asin
i i
P P h h
h r y
,
2
2
1
dP
dh
y
(9)
với yi-1 = (hi-1 - yc)/r.
3.4. Cung e-líp
Kí hiệu Ei(a, b, xc, yc; hi-1, hi) là cung e-líp
từ hi-1 đến hi với tâm tại (xc,yc) và các bán
trục theo phương x và y lần lượt là a và b.
Đặt y = (h - yc)/b là độ sâu tương đối.
Độ rộng mặt nước và đạo hàm
2
2 2 1
c
T x a y
,
2
21
dT a y
dh b
y
(10)
Diện tích mặt cắt ướt
1 1
2
,
2 asin 1
i i
c
A A h h
h x h ab y y y
(11)
Chu vi ướt và đạo hàm
1 1
i i
P P h h
,
2
2 E ,h a k
,
2 2
2 2
11
dP a y
dh b y
(12)
Trong đó
2 2 2
0
E , 1 sin
k k t dt
(13)
là hàm tích phân eliptic khuyết loại II, k là
tâm sai hay độ dẹt của ellíp, φ là góc biên độ.
2
2
2
1
a
k
b
,
asin
y
(14)
Tuyển tập Hội nghị Khoa học thường niên năm 2018. ISBN: 978-604-82-2548-3
356
3.5. Ví dụ mặt cắt móng ngựa tiêu chuẩn
Mặt cắt móng ngựa tiêu chuẩn có B = H =
2r được hợp thành từ 4 cung tròn gồm 3 bộ
phận mặt cắt (Hình 1): C1(2r; 0,2r; 0,h1),
C2(2r; -r,r; h1,r) và C3(r; 0,r; r,2r) với
3 7
1 2
h r
. Thay các thông số của các cung
này vào (7) - (9) sẽ nhận được biểu thức
tường minh để tính toán thủ công các đặc
trưng mặt cắt như sau.
Với 0 ≤ h ≤ h1, có y = (h/2r - 1), y0 = -1 và
2
4 1
T r y
,
2
4 asinP r y
,
2 2
2
4 asin 1
A r y y y
(15)
Tại h = h1 ≈ 0.177r có
1 7
4
y
và
1
1, 646T r
, 1
1,696P r
,
2
1
0,196A r
(16)
Với h1 ≤ h ≤ r, có y = (h - r)/2r,
1
1 7
1
2 4
h r
r
y
và
2
2 4 1
T r r y
,
1 1
4 asin asin
P P r y y
,
2
1 1 1
2 2 2
1 1
2 4 asin asin
4 1 1
A A r h h r y y
r y y y y
(17)
Tại h = r có y = 0 và
2
2T r
, 2
3,392P r
,
2
2
1,747A r
(18)
Với r ≤ h ≤ 2r, có y = (h/r - 1), y1 = 0 và
2
2 1
T r y
,2
2 asinP P r y
,
2 2
2asin 1
A A r y y y
(19)
Tại h = H = 2r có y = 1 và
3
0
T
, 3
6,534P r
,
2
3
3,317A r
(20)
3.6. Phần mềm tính toán
Một phần mềm tính toán các đặc trưng mặt
cắt ngang đã được xây dựng sử dụng ngôn
ngữ lập trình C#. Phần mềm có thể tính toán
các mặt cắt bất kỳ được xây dựng từ 4 loại
cung cơ bản ở trên, từ mặt cắt đơn giản hình
thang, chữ nhật, parabol, e-líp đến các mặt
cắt phức tạp được kết hợp từ 4 loại cung cơ
bản này. Trong phần mềm đã được định
nghĩa sẵn các kích thước định hình của gần
30 dạng mặt cắt trong đó có các mặt cắt dạng
móng ngựa, quai giỏ, hình trứng, hình diều,
hình quả lê, hình ô-van, các dạng vòm, v.v…
Phần mềm có ưu điểm là có thể tính toán
các đặc trưng mặt cắt một cách tổng quát sử
dụng các công thức (1) - (14) mà không cần
dạng công thức tường minh như (15) - (20).
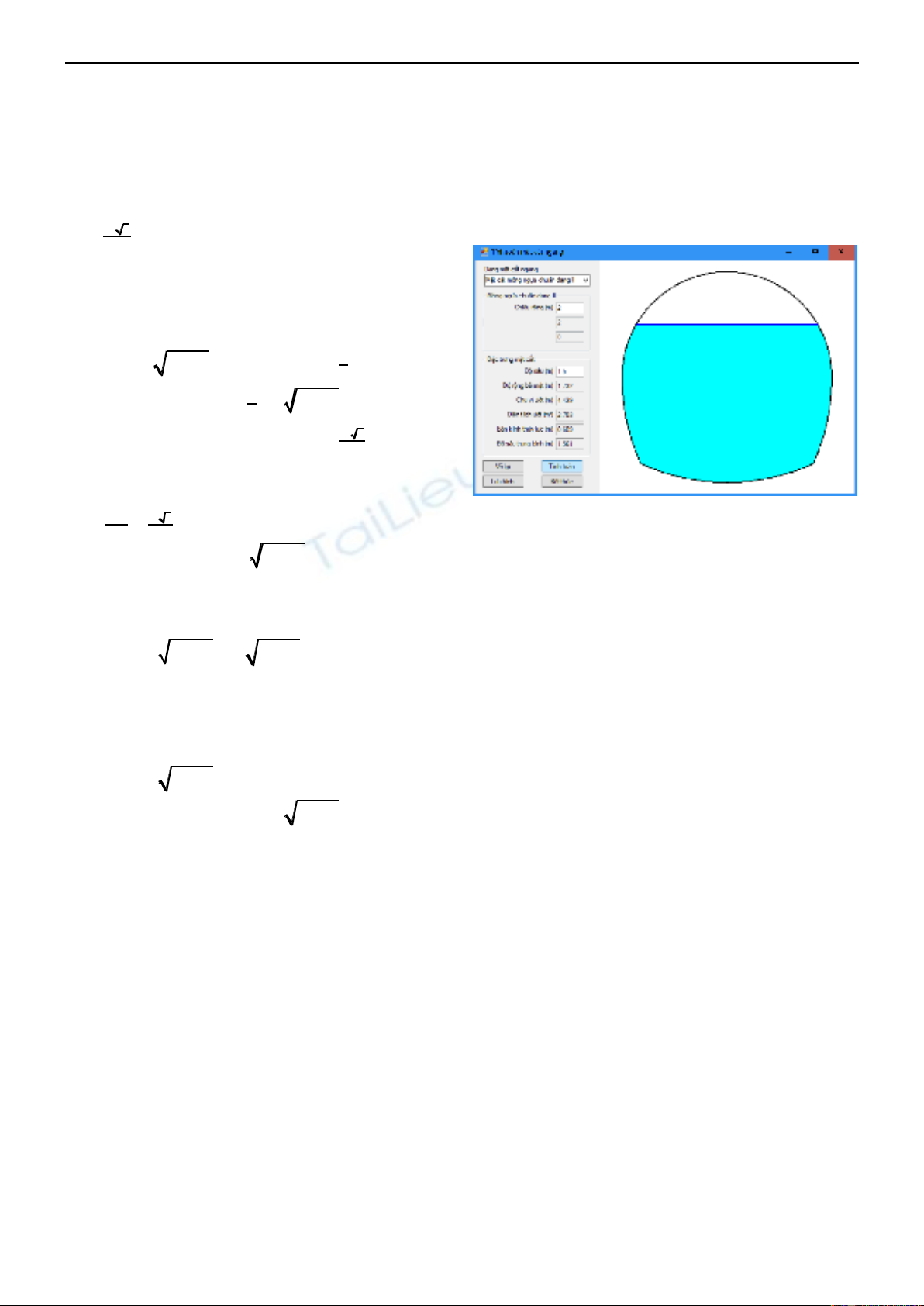
Ví dụ giao diện tính toán cho mặt cắt
móng ngựa tiêu chuẩn với như Hình 2.
Hình 1. Giao diện phần mềm với ví dụ
cho mặt cắt móng ngựa tiêu chuẩn
4. KẾT LUẬN
Bài báo đã trình bày một tiếp cận tổng quát
để tính toán chính xác các đặc trưng mặt cắt
ngang cho các loại mặt cắt ngang bất kỳ hợp
thành từ các cung cơ bản là đoạn thẳng, cung
tròn, parabol và e-líp. Tiếp cận này đã được
xây dựng thành phần mềm tính toán với gần 30
loại mặt cắt ngang thông dụng đã được định
nghĩa sẵn.
5. TÀI LIỆU THAM KHẢO
[1] Merkley, G.P. (2005). Standard horseshoe
cross section geometry. Agricultural Water
Management. 71: 61–70.
[2] Samani, H.M.V. et al. (2013). Evaluating
velocity and discharge in horseshoe and D-
shape cross sections. J. Basic and Applied
Sci. Res. 3(2): 996-1004.
[3] Wei, B., Wang Z., Meng W., Liu Y. (2012).
The calculation and application for free flow
tunnel of normal depth and critical depth. J.
Water Res. and Hydr. Eng. 1(1): 27-30.
[4] Wen, H., and Li, F. (2013). Simplified
calculation method of normal water depth on
II type horseshoe tunnel with flat–bottom.
App. Mec. and Mat. 353-356: 1353-1358.