Tiết 38: BÀI TẬP ĐƯỜNG THẲNG VUÔNG GÓC MẶT PHẲNG
I. Mục tiêu:
1. Kiến thức:
-Củng cố lại kiến thức về đường thẳng vuông góc mặt phẳng.
-Điều kiện để đường thẳng vuông góc mặt phẳng, vận dụng chứng minh
đường thẳng vuông góc đường thẳng, đường thẳng vuông góc mặt phẳng,
xác định mặt phẳng.
-Xác định gócc giữa đường thẳng và mặt phẳng.
2. Kỷ năng:
-Vận dụng để tính góc giữa đường thẳng và mặt phẳng.
-CM các BT về hai đường thẳng vuông góc.
3. Thái độ:
Cẩn thận, chính xác.
II. Chuẩn bị:
GV: Phiếu học tập(TN)
HS: Điều kiện để đường thẳng vuông góc mặt phẳng, phương pháp CM đường
thẳng vuông góc mặt phẳng.
III. Phương pháp:
Gợi mở vấn đáp, đan xen hoạt động nhóm.
IV. Tiến trình bài học:
Hoạt động của giáo viên Hoạt động của học sinh
*HĐ1:
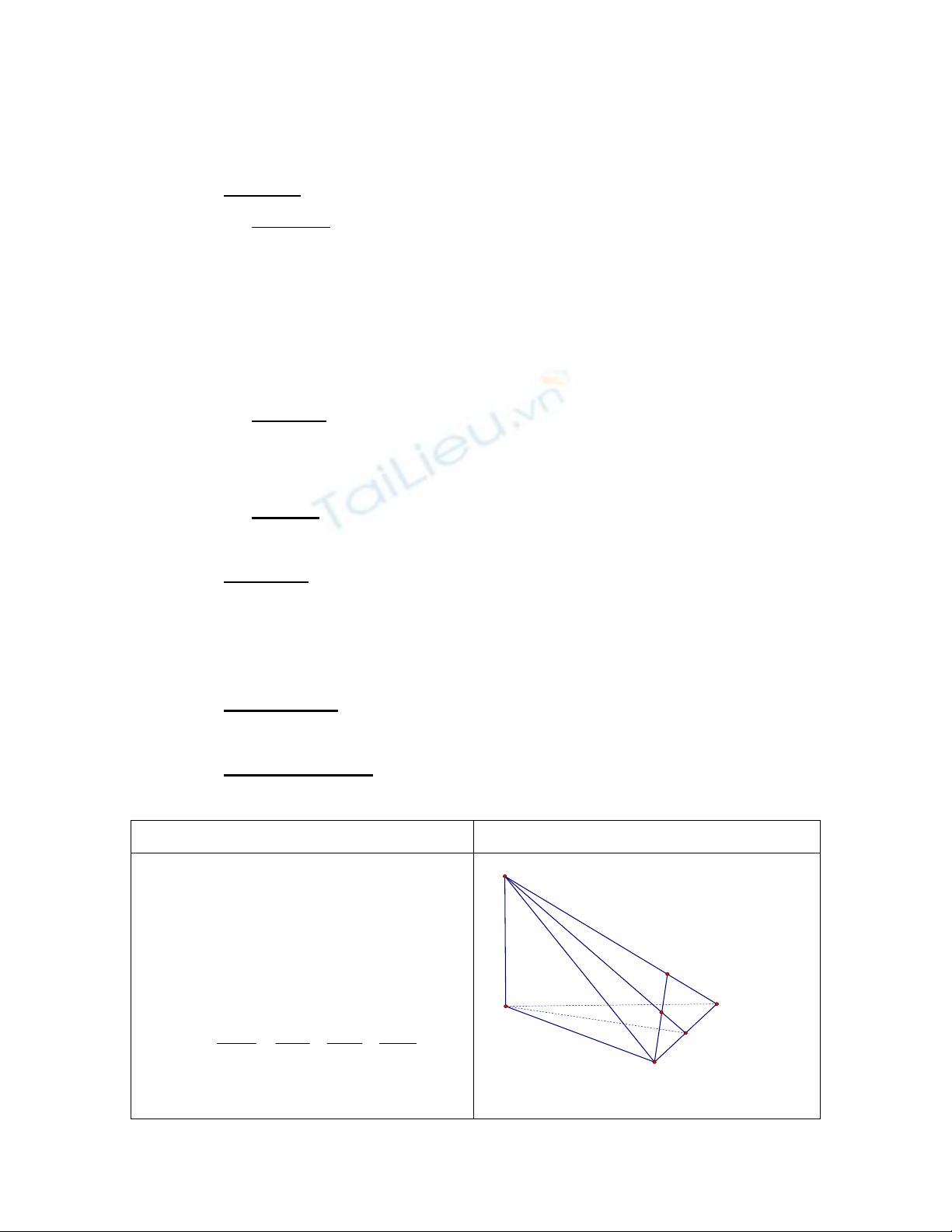
Bài 1(Bài 17_SGK):
Cho OA, OB, OC đôi một vuông góc. H là
trực tâm của
ABC
. Chứng minh:
a.
( )
OH ABC
b.
2 2 2 2
1 1 1 1
OH OA OB OC
-H1: Nêu phương pháp chứng minh đường
H
M
OA
B
C
-CM OH vuông góc với hai đường thẳng
thẳng OH vuông góc mặt phẳng (ABC)?
-GV gới ý, đôn đốc, kiểm tra
-H2: Nêu tính chất đường cao xuất phát tư
đỉnh góc vuông của tam giác vuông?
Áp dụng cho
?
Từ đó…?
*HĐ 2(Bài 18_SGK)
a. H1: AH là đường cao tam giác ABC, suy
ra?
H2: Giả sử AH cắt BC tai A’, xét vị trí
tương đối SA’ và BC? Vậy SA’ là đường
gì?
H3: Từ đó em có kết luận gì?
cắt nhau trong (ABC)
O
*CM:
( )
OH AB
OH ABC
OH AC
2 2 2
1 1 1
OH OC OM
-TL:
2 2 2
1 1 1
OM OA OB
-
2 2 2 2
1 1 1 1
OH OA OB OC
-TL:
AH BC
-TL:
' '
SA BC SA
là đường cao.
Vậy AH, SK, BC đồng quy tại A’
O
C M
H
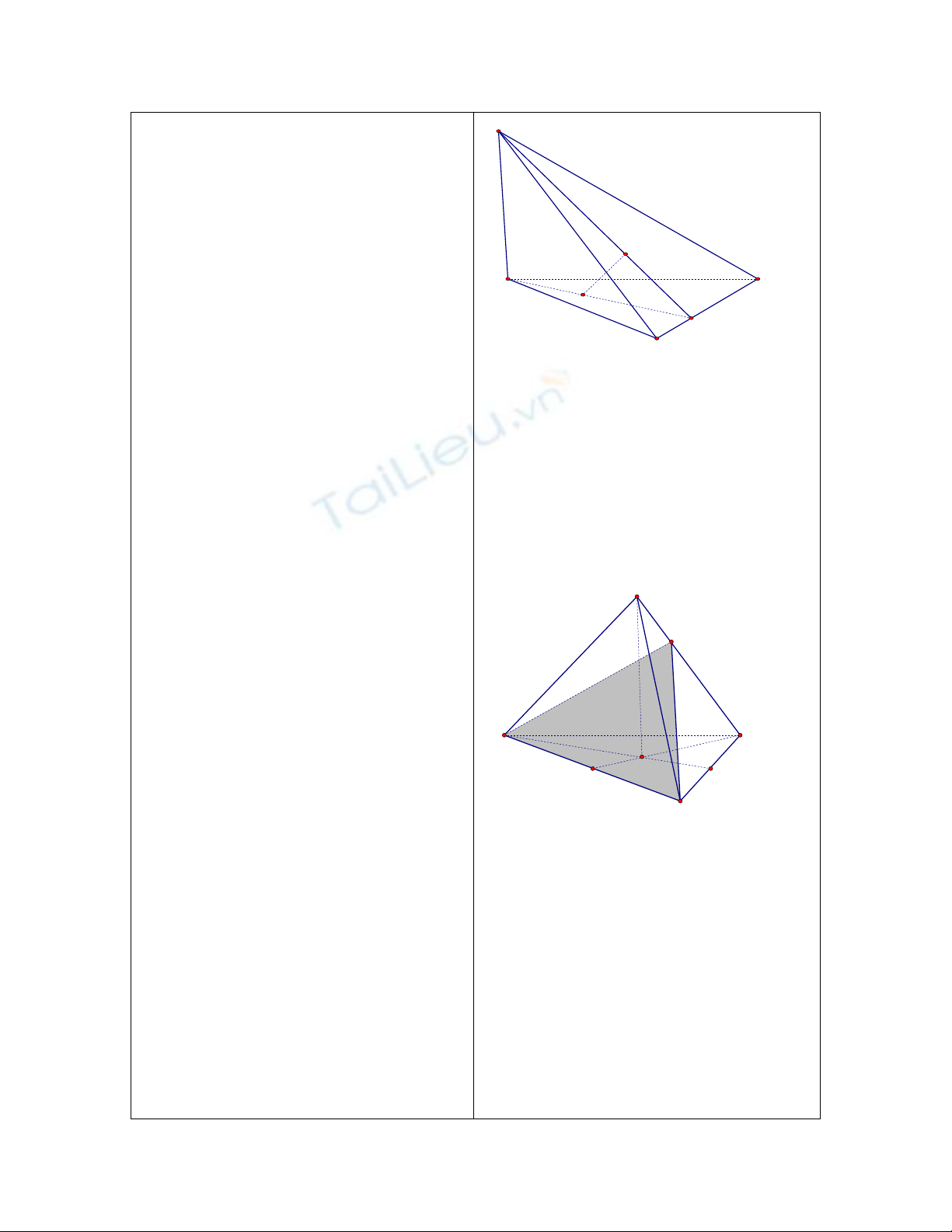
b. Giải tương tự bài 1
c. Giải tương tự bài 1
HĐ3: Bài 19_SGK
a. CM
( )
SG ABC
: Tương tự bài 1
b. HD:
H1: Khi nào thì chân đường cao C1 hạ từ A
của
SAC
nằm giữa SC? Nêu liên hệ giữa
a và b?
H2: Tính diện tích
1
ABC
?
S
A
C
B
A'
H
K
Làm việc theo nhóm(1bàn) trong vòng 10’.
·
2 2 2 2 2
ASC 90 2
o
AC SA SC a b
-Trình bày kết quả.
G
C'
A
C
B
S
C1
Bài 4(TN):
GV phát phiếu HT(kèm theo)
Hết giờ, GV gọi từng nhóm trả lời kết quả
và cho biết tai sao lại chọn phương án đó.
BÀI TẬP TRẮC NGHIỆM
Câu1: Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b vuông góc với
mặt phẳng (P). Kết quả nào sau đây đúng?
A. a cắt b B. a song song b C. a trùng b D. B hoặc C
Câu 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và (Q). Chọn kết quả đúng.
A. (P)//(Q) B. (P) cắt (Q) C. (P) trùng (Q) D. A hoặc C
Câu3: Đường thẳng a vuông góc với mặt phẳng (P), c chứa trong (P). Kết quả sau đây
đúng?
A. a//c B. a trùng c C. a vuông góc c D. a cắt c
Câu 4: Cho điểm A và đường thẳng a. Qua A có bao nhiêu mặt phẳng vuông góc với a?
A. 0 B. 1 C. 2 D. vô số
Câu 5: Cho hai đường thẳng a và b. Qua a có bao nhiêu mặt phẳng vuông góc với đường
thẳng b?
A. 0 B. 1 C. vô số D. A hoặc B
Câu 6: Cho đường thẳng a vuông góc với đường thẳng b, đường thẳng a vuông góc với
mặt phẳng (P). Vị trí tương đối của b và (P) là:
A. b//(P) B. B vuông góc (P) C. b chứa trong (P) D. A hoặc C
Câu 7: Cho hình chóp S.ABC, SA vuông góc với (ABC), tam giác ABC vuông tại B.
Cho SA=3cm, AB=4cm, BC=
11
cm thì SC bằng:
A. 4cm B. 5cm C. 6cm D. 7cm
Câu 8: Cho hình chóp S.ABC, SA vuông góc với (ABC), đáy ABC là tam giác đều cạnh
a, SA=a, Mlà trung điểm BC. Tính SM?
A.
5
2
a B.
6
2
a C.
7
2
a D.
8
2
a
Câu 9: Cho tứ diện OABC có OA=OB=OC=a, OA, OB, OC đôi một vuông góc. Khẳng
định nào sau đây sai?
A.
ABC
đều có cạnh bằng
2
a
B.
( )
OA OBC
C. Gọi H là hình chiếu của O lên (ABC),
3
2
a
OH
D. H là trọng tâm
ABC
Câu 10: Cho hình chóp đều ABCD có đáy BCD là tam giác đều cạnh a tâm O, cạnh bên
6
3
a. Tính góc giữa cạnh bên và mặt đáy.
A. 45o B. 30o C. 60o D. Một kết quả khác
V. Củng cố và hướng đẫn học tập ở nhà:
-Xem lai phương pháp chứng minh đường thẳng vuông góc đường thẳng và
đường thẳng vuông góc mặt phẳng.
-BTVN: Các bài tập còn lại