Tiết 6 GIỚI HẠN CỦA HÀM SỐ (tt)
A. Mục tiêu: Qua bài học học sinh cần hiểu được:
1. Về kiến thức:
+ Biết định nghĩa giới hạn một bên của hàm số và định lý của nó .
+ Biết định nghĩa giới hạn hữu hạn của hàm số tại vô cực.
2. Về kỹ năng:
+ Biết vận dụng định nghĩa vào việc giải một số bài toán đơn giản về
giới hạn của hàm số.
+ Biết vận dụng các định lý về giới hạn của hàm số để tính các giới
hạn đơn giản.
B. Chuẩn bị của thầy và trò:
1. Chuẩn bị của trò: Làm bài tập ở nhà và xem trước bài mới.
2. Chuẩn bị của thầy: Giáo án
C. Phương pháp dạy học:
+ Nêu vấn đề,đàm thoại.
+ Tổ chức hoạt động nhóm.
D. Tiến trình bài cũ:
1. Ổn định lớp
2. Kiểm tra bài cũ: Thông qua các hoạt động trong giờ học.
3. Bài mới
Hoạt động của HS Hoạt động của GV Nội dung ghi bảng
Nghe và chép bài
H: Sử dụng công thức
(2)
152
)5(lim)(lim
2
2
2
2
xxf x
x
H: Sử dụng công thức
(1)
1042.3
)43(lim)(lim 2
2
xxf x
x
Vậy )(lim
2xf
x không
GV giới thiệu giới hạn
một bên.
H: Khi
2x thì sử
dụng công thức nào ?
H:
2)(lim
x
xf = ?
H: Khi
2x thì sử
dụng công thức nào ?
H:
2)(lim
x
xf = ?
H: Vậy )(lim
2xf
x = ?
3. Giới hạn một bên:
ĐN2: SGK
ĐL2: SGK
Ví dụ: Cho hàm số
)
2(25
)
1(243
)( 2xkhix
xkhix
xf
Tìm
2)(lim
x
xf ,
2)(lim
x
xf ,
)(lim
2xf
x ( nếu có ).
Giải:
tồn tại vì
2)(lim
x
xf
2)(lim
x
xf
)(lim)(lim
1)(lim
22
2
xfxf
xf
xx
x
Do đó cần thay số 4
bằng số -7
)(xf dần tới 0
H: Trong biểu thức (1)
xác định hàm số
)(xfy
ở ví dụ trên
cần thay số 4 bằng số
nào để hàm số có giới
hạn là -1 khi 2
x?
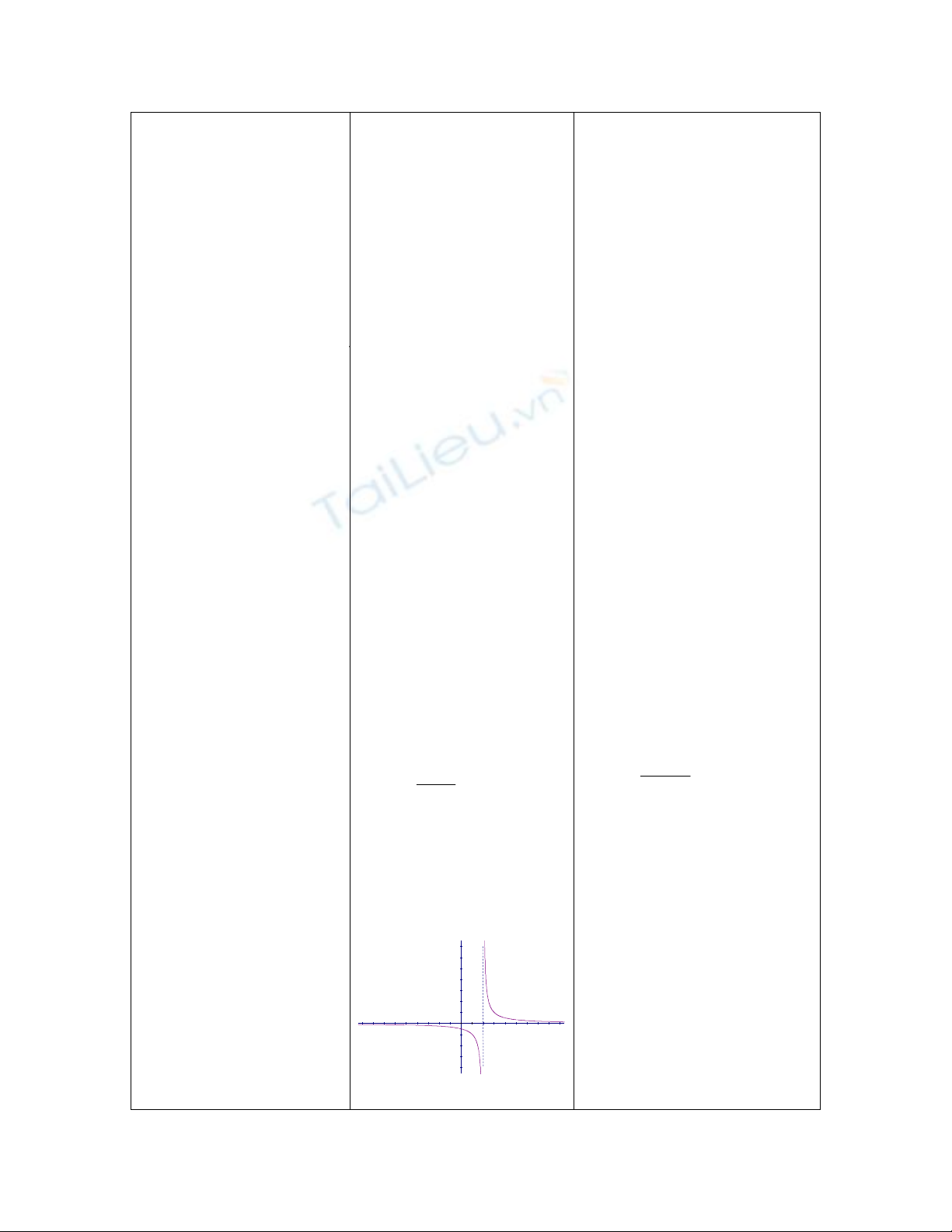
Cho hàm số
2
1
)(
x
xf có đồ thị
như hvẽ
6
4
2
-2
5
1042.3
)43(lim)(lim 2
2
xxf x
x
1042.3
)43(lim)(lim 2
2
xxf x
x
Vậy )(lim
2xf
x không tồn
tại vì
2)(lim
x
xf
2)(lim
x
xf
II. Giới hạn hữu hạn của
hàm số tại vô cực:
ĐN 3: SGK
Ví dụ: Cho hàm số
1
23
)(
x
x
xf . Tìm
)(lim xf
x và )(lim xf
x .
Giải:
Hàm số đã cho xác định
trên (-
; 1) và trên (1;
+
).
)(xf dần tới 0
Hàm số trên xác định
trê n (-
; 1) và trên
(1; +
).
HS nêu hướng giải và
lên bảng làm.
H: Khi biến
x
dần tới
dương vô cực, thì
)(xf dần tới giá trị nào
?
H: Khi biến
x
dần tới
âm vô cực, thì )(xf dần
tới giá trị nào ?
GV vào phần mới
H: Tìm tập xác định
của hàm số trên ?
H: Giải như thế nào ?
Giả sử ( n
x) là một dãy số
bất kỳ, thoả mãn n
x< 1 và
n
x.
Ta có
1
3
lim
1
23
lim)(lim
n
n
nx
x
xf
Vậy
3
1
23
lim)(lim
 x
x
xf xx
Giả sử ( n
x) là một dãy số
bất kỳ, thoả mãn n
x> 1 và
n
x.
Ta có:
1
3
lim
1
23
lim)(lim
n
n
nx
x
xf
Vậy
3
1
23
lim)(lim
 x
x
xf xx
cc
x

lim
Với c, k là các hằng số
Chú ý:
a) Với c, k là các hằng số
và k nguyên dương, ta
luôn có :
cc
x

lim ;
0lim
 k
xx
c.
b) Định lý 1 về giới hạn
hữu hạn của hàm số khi
0
xx vẫn còn đúng khi

x
hoặc

x
Ví dụ: Tìm 2
35
lim 2
2
 x
xx
x
Giải: Chia cả tử và mẫu
cho 2
x, ta có:
2
35
lim 2
2
 x
xx
x=
2
2
1
3
5
lim
x
x
x
 = )
2
1(lim
)
3
5(lim
2
x
x
x
x

 =
2
2
lim1lim
3
lim5lim
x
x
xx
xx


=5
0
1
05